Понимание четвертого центрального момента случайной величины и его применение в статистике
Четвертый центральный момент случайной величины представляет собой важную характеристику распределения, которая помогает оценить степень асимметрии и пиковости данных. В данном разделе мы рассмотрим, как правильно вычислить этот момент и какие выводы можно сделать на основе его значений. Также мы предоставим полезные советы, которые помогут вам лучше понять эту статистическую характеристику и ее значение для анализа данных.

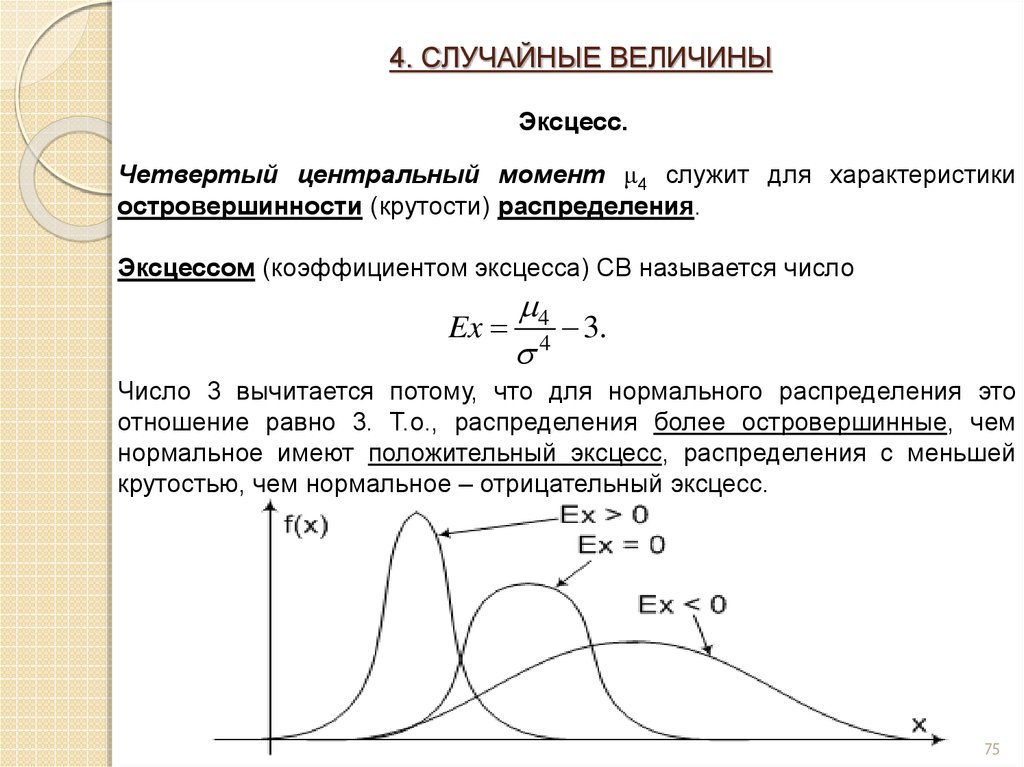

Для вычисления четвертого центрального момента необходимо найти математическое ожидание величины, возведенной в четвертую степень, и вычесть из этого значение четвертой степени математического ожидания случайной величины.

Теория вероятностей #13: Моменты случайной величины / дисперсия, стандартное отклонение, асимметрия


Четвертый центральный момент часто используется для оценки куртоза распределения, который помогает определить, насколько острыми или плоскими являются хвосты распределения.

Теория вероятностей #14: математ. ожидание, дисперсия, медиана, мода, начальные моменты
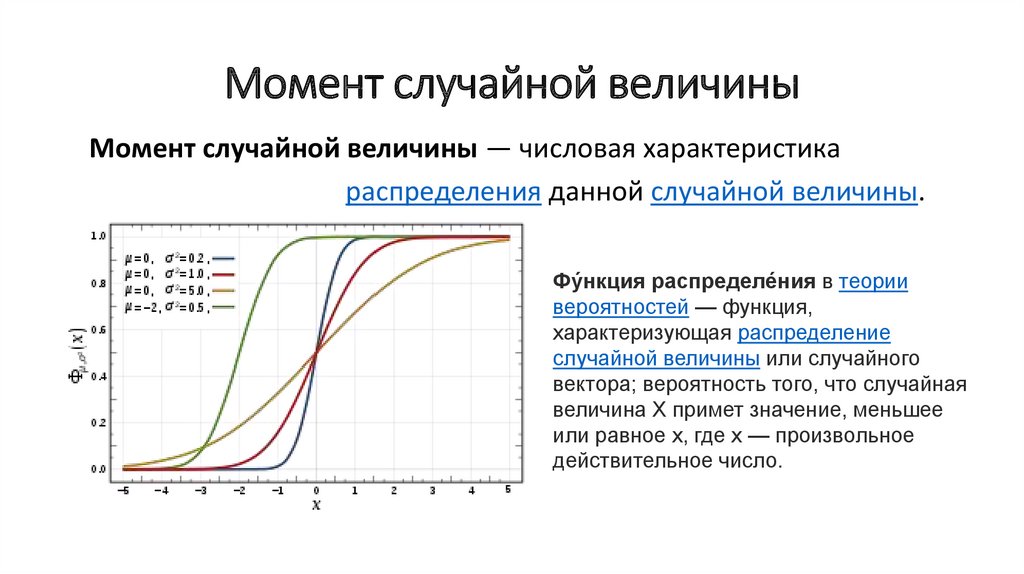
При анализе данных не забудьте учитывать, что большое значение четвертого центрального момента может указывать на высокую вероятность экстремальных значений (внезапных выбросов).

10 Дискретные случайные величины Задачи

Если четвертый центральный момент близок к нулю, это может свидетельствовать о том, что распределение данных близко к нормальному, с умеренной концентрацией в хвостах.
Дискретные случайные величины. Математическое ожидание и дисперсия.

Четвертый центральный момент не является независимым, его значение зависит от других статистических характеристик, таких как среднее значение и дисперсия.
Видеолекция 5-4 ТВиМС Тема №5 Закон распределения дискретных случайных величин Пример


Для более точного анализа используйте нормализацию четвертого центрального момента, разделив его на квадрат дисперсии, чтобы получить безразмерную величину — куртоз.

Переделали старую избу с печью в большой семейный дом: про дом, участок и реставрацию / Sewera
При работе с реальными данными важно учитывать, что наличие выбросов может сильно повлиять на значение четвертого центрального момента.

Прогноз на 2025 год от нумеролога Кристины Егиазаровой

Четвертый центральный момент можно использовать для построения более сложных моделей статистического анализа, например, для оценки риска в финансовых приложениях.
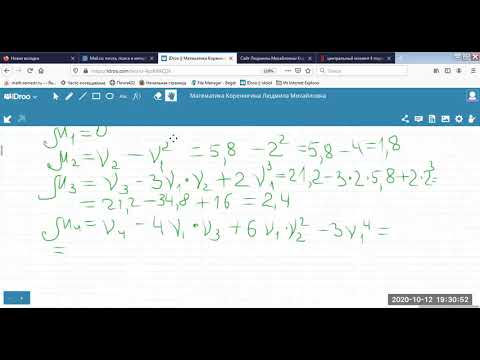
Видео Лекция 4-7 ТВиМС Тема 4 Начальные и центральные моменты случайных величин


Когда четвертый центральный момент значительно отличается от теоретического значения для нормального распределения, это может сигнализировать о необходимости применения других моделей распределений.

Понимание и правильное использование четвертого центрального момента позволяет более глубоко анализировать и интерпретировать данные, выявляя важные особенности распределений.

21. Случайные величины
