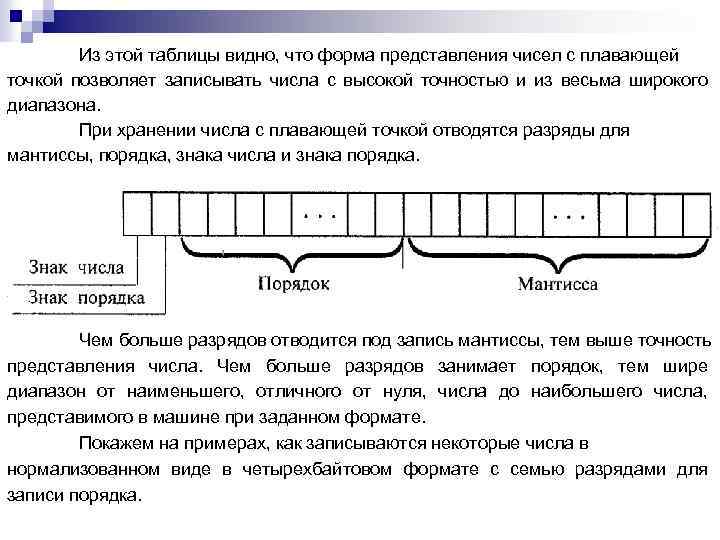
Как различные факторы влияют на точность представления чисел в цифровых вычислениях

Точность представления чисел в вычислительных системах играет ключевую роль в различных областях, таких как программирование, численные вычисления и моделирование. Ошибки, связанные с ограничениями форматов чисел, могут приводить к значительным погрешностям в расчетах, что важно учитывать при разработке алгоритмов и программных решений.

Используйте типы данных с большей точностью, такие как double вместо float, чтобы минимизировать ошибки округления.

Понимание особенностей форматов представления чисел (например, IEEE 754) помогает избежать неожиданных погрешностей при вычислениях с плавающей запятой.

Проводите тестирование с различными входными данными, чтобы выявить возможные погрешности в вычислениях, связанные с потерей точности.

Для работы с очень большими числами используйте библиотеки, поддерживающие произвольную точность, такие как GMP или BigDecimal.

При необходимости работать с малыми числами используйте нормализацию данных для уменьшения влияния ошибок округления.

Использование символьных вычислений может быть полезно для получения более точных результатов в аналитических задачах.

Для критически точных вычислений избегайте операций с числами, близкими к пределу точности типа данных.

Учитывайте погрешности при работе с результатами в численных методах и учитывайте их в интерпретации результатов.

Не забывайте об ошибках округления, которые могут накапливаться при многократных вычислениях и влиять на окончательные результаты.

При реализации алгоритмов важно проверять их устойчивость к ошибкам представления чисел, особенно при многократных операциях с малыми значениями.