Методы расчета площади усеченного конуса: полезные советы и стандартные формулы
Усеченный конус - это геометрическая фигура, которая образуется в результате отсечения верхней части обычного конуса плоскостью. Он имеет два основания - большее и меньшее, а также боковую поверхность. Правильное вычисление площади усеченного конуса может быть полезным для решения различных задач в физике, строительстве или инженерии.
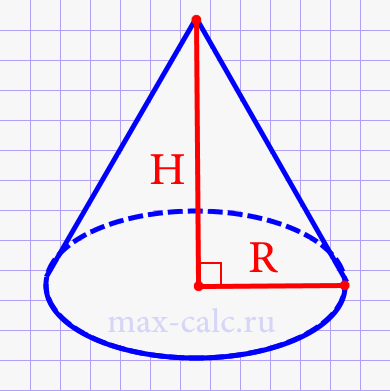
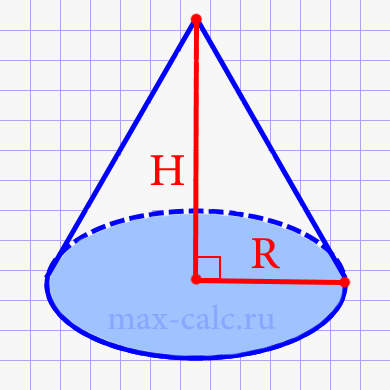
При вычислении площади усеченного конуса учтите, что для каждого основания необходимо знать радиус.

Усеченный конус. Практическая часть. 11 класс.
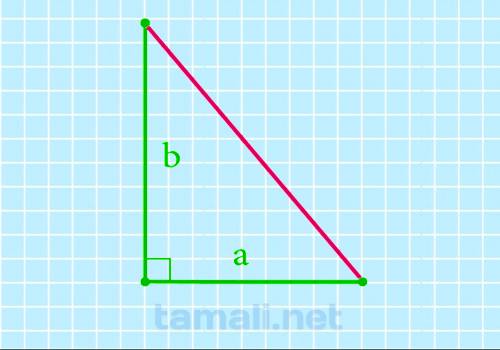
Для получения точного результата рекомендуется использовать более точные значения и не округлять их в промежуточных вычислениях.

ГЕОМЕТРИЯ 11 класс: Конус Площадь конуса. Усеченный конус
Если у вас нет точных значений радиусов, можно использовать приближенные значения, но в этом случае решение будет менее точным.

Конус на токарном станке ,вычисление угла и изготовление
Используйте формулу для вычисления площади боковой поверхности усеченного конуса: S = π (r1 + r2) l, где r1 и r2 - радиусы оснований, l - образующая конуса.

Усеченный конус. 11 класс.
Если у вас есть только значения высоты конуса и радиуса меньшего основания, вычислите радиус большего основания с помощью формулы: r2 = r1 + (h2/r1) * (r1 - r).
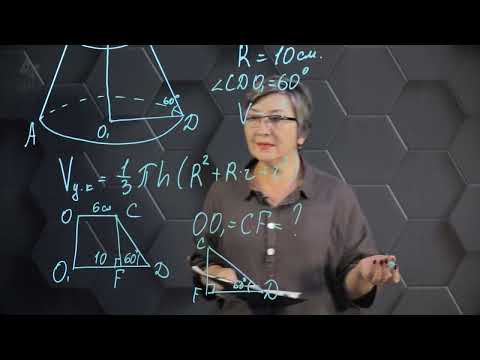
Усеченный конус. Практическая часть. 11 класс.


Чтобы проверить правильность решения, можно воспользоваться онлайн-калькулятором для вычисления площади усеченного конуса.


Не забывайте, что значения радиусов и высоты должны быть в одних и тех же единицах измерения.

Геометрия. 11 класс. Усеченный конус и его элементы. Площадь поверхности усеченного конуса
При работе с усеченным конусом обратите внимание на формулы для вычисления объема и диаметров оснований.

Как легко сделать усеченный конус (конус) из металла 2 мм. Сделай сам!
Если у вас возникли сложности с вычислением площади усеченного конуса, обратитесь к учебникам или справочной литературе.
Жестяные работы. Усечённый конус. Расчет усечённого конуса с онлайн калькулятора - ссылка⬇️


Запишите все промежуточные вычисления, чтобы не потеряться в процессе решения задачи.