Как найти значение производной функции в заданной точке: простые шаги и примеры
Значение производной функции в точке играет ключевую роль в анализе поведения функции. Это значение показывает, как быстро изменяется функция вблизи данной точки. Процесс нахождения производной является основой для множества применений в математике, физике и других областях. В данной статье рассмотрим основные моменты, которые помогут вам понять и правильно вычислять производные на примерах.
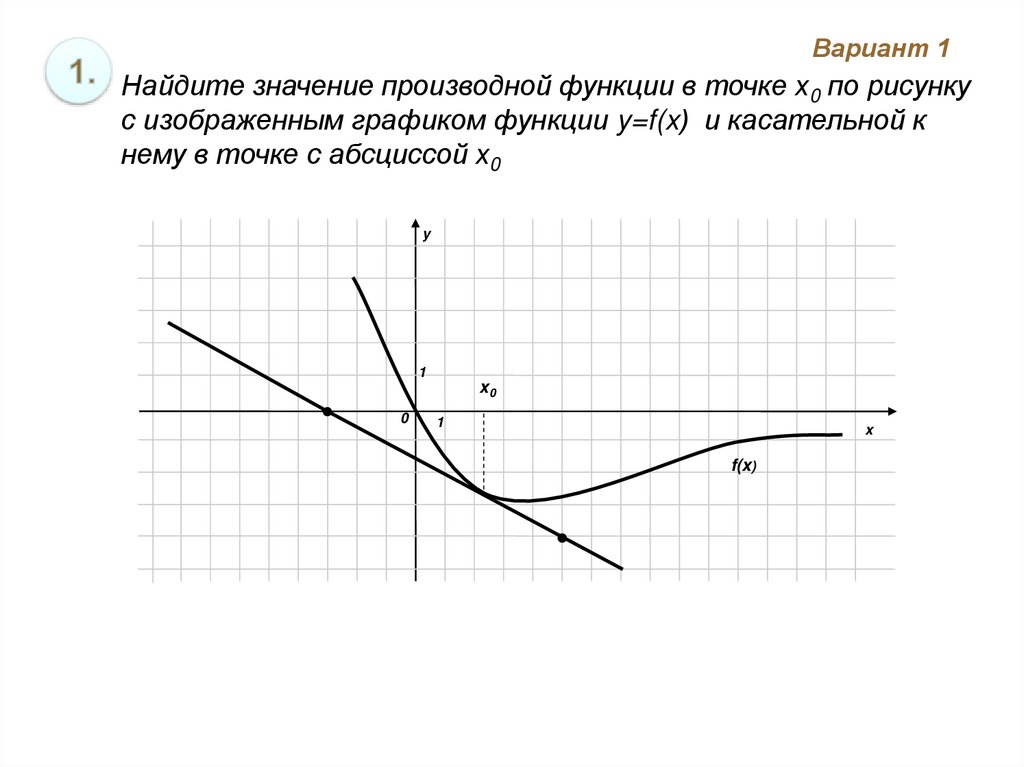
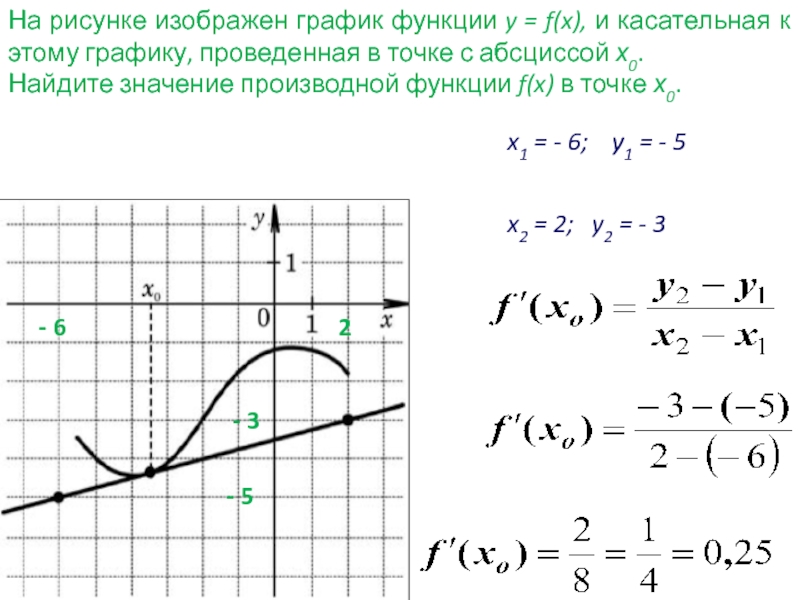
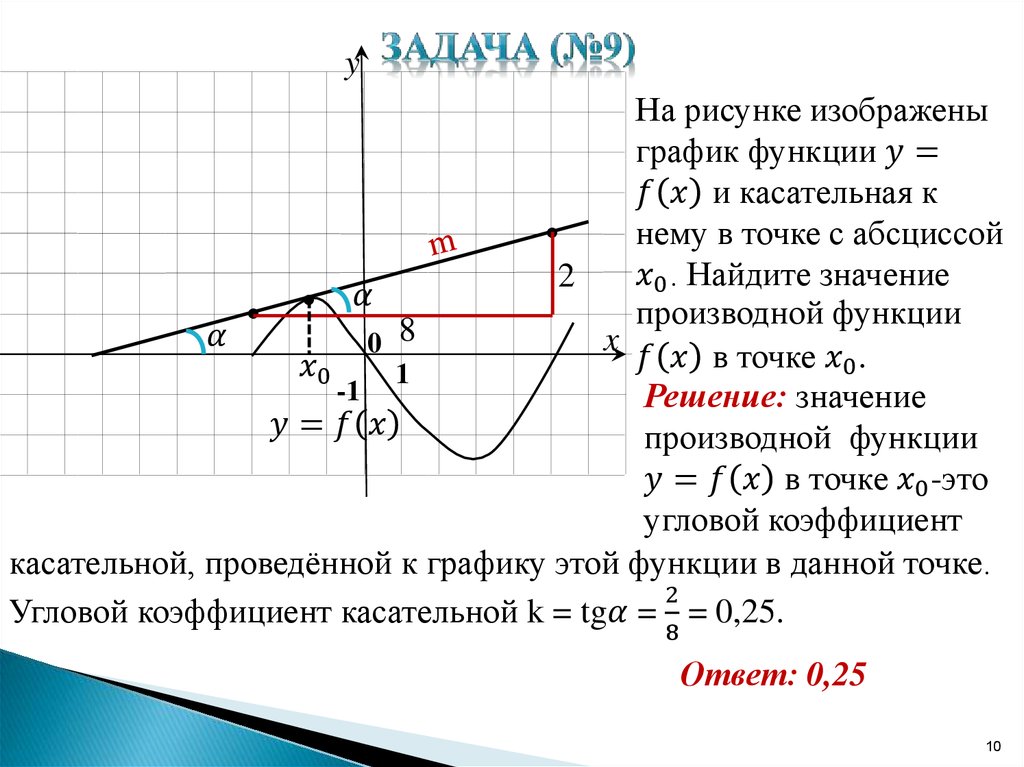
При нахождении производной важно помнить, что она представляет собой мгновенную скорость изменения функции.
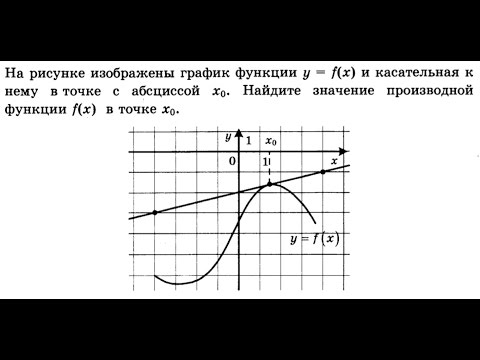
ЕГЭ 2017 Профильный №7 найти производную в точке касания #7
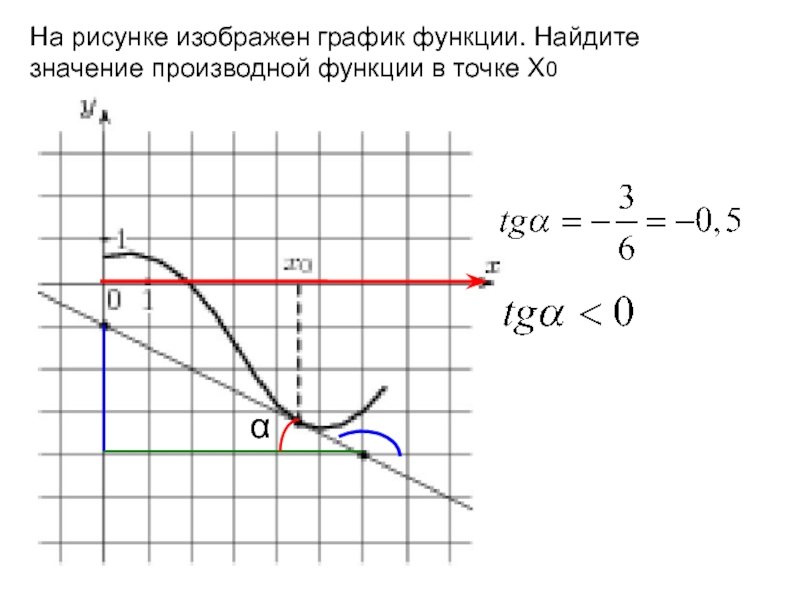
Если функция непрерывна и дифференцируема в точке, то производная в этой точке существует и может быть вычислена через предел.

Дифференциальные уравнения. Шилин И. С.

Для вычисления производной функции в точке часто используется правило дифференцирования и таблица производных стандартных функций.

Геометрический смысл производной - Касательная
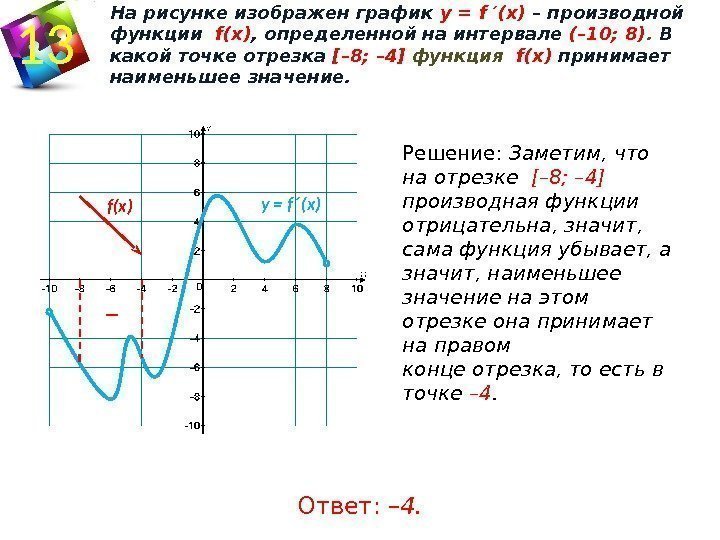
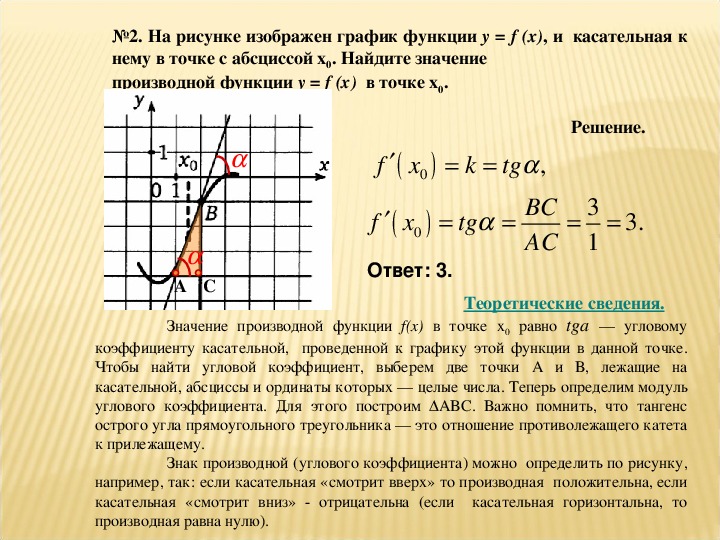
Для нахождения производной можно воспользоваться определением производной через предел, что даст точное значение на конкретной точке.

Производная в точке. Алгебра 10 и 11 класс.
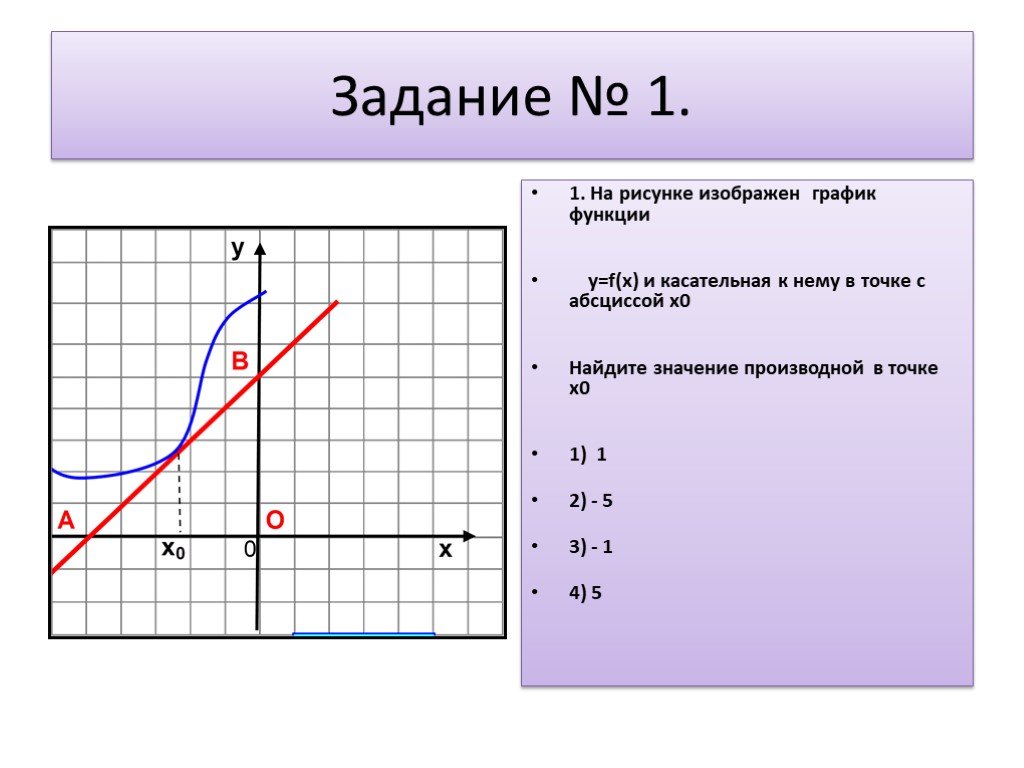
Для сложных функций можно применять цепное правило, которое позволяет дифференцировать составные функции.
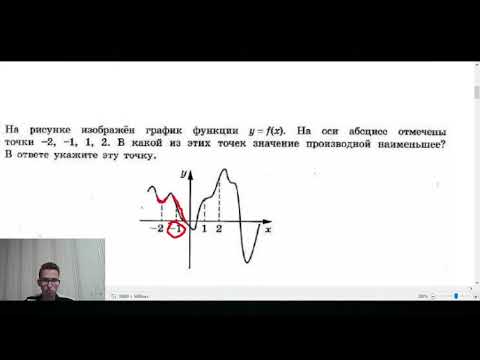
В какой точке значение ПРОИЗВОДНОЙ наименьшее?

Производная функции в точке может помочь определить её поведение в окрестности этой точки, например, нахождение экстремумов.

АЛГЕБРА С НУЛЯ — Что такое Производная?


Если производная функции в точке равна нулю, это может свидетельствовать о наличии экстремума в этой точке.
Производная функции. 10 класс.

В случае, если производная не существует в точке, функция может иметь разрыв или не быть гладкой в данной точке.
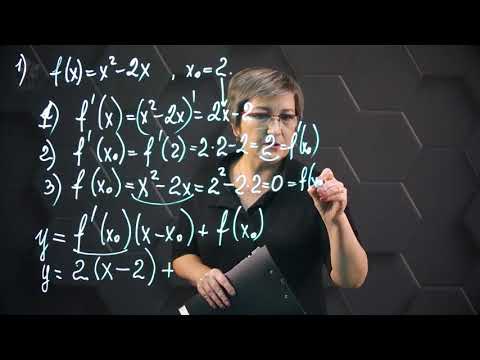
Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.
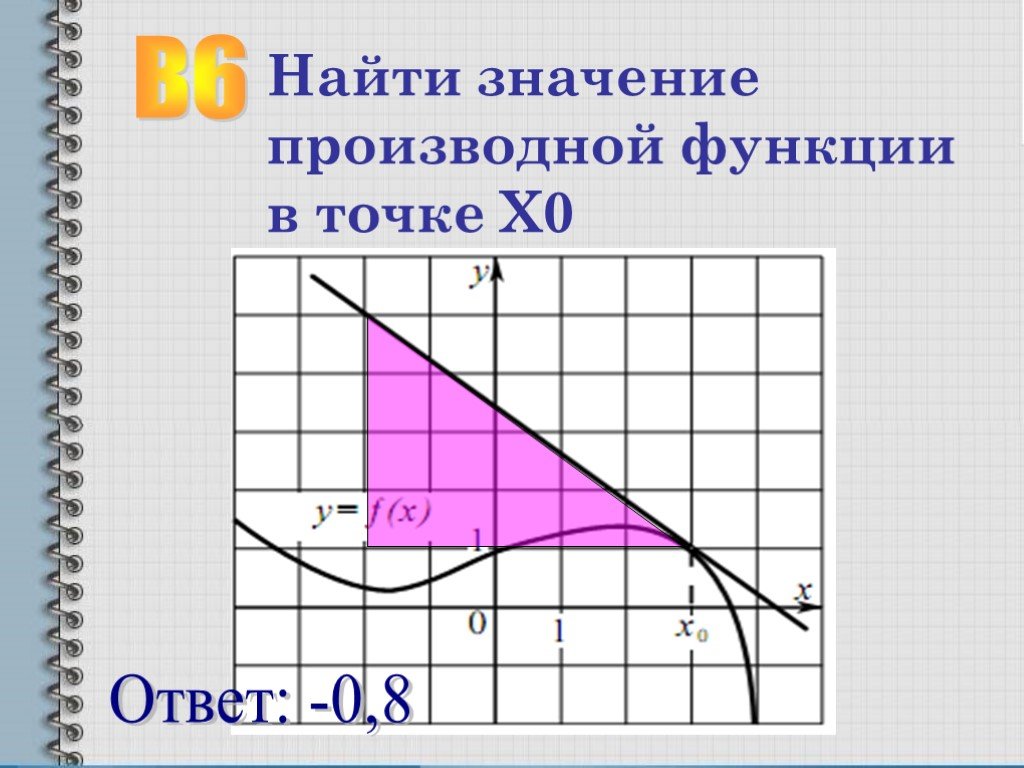
Изучая поведение производной, можно сделать выводы о том, как изменяется функция, и предсказать её поведение на больших интервалах.
Для анализа поведения функции важно понимать взаимосвязь между производной и её графиком: где производная положительна, функция возрастает, где отрицательна — убывает.