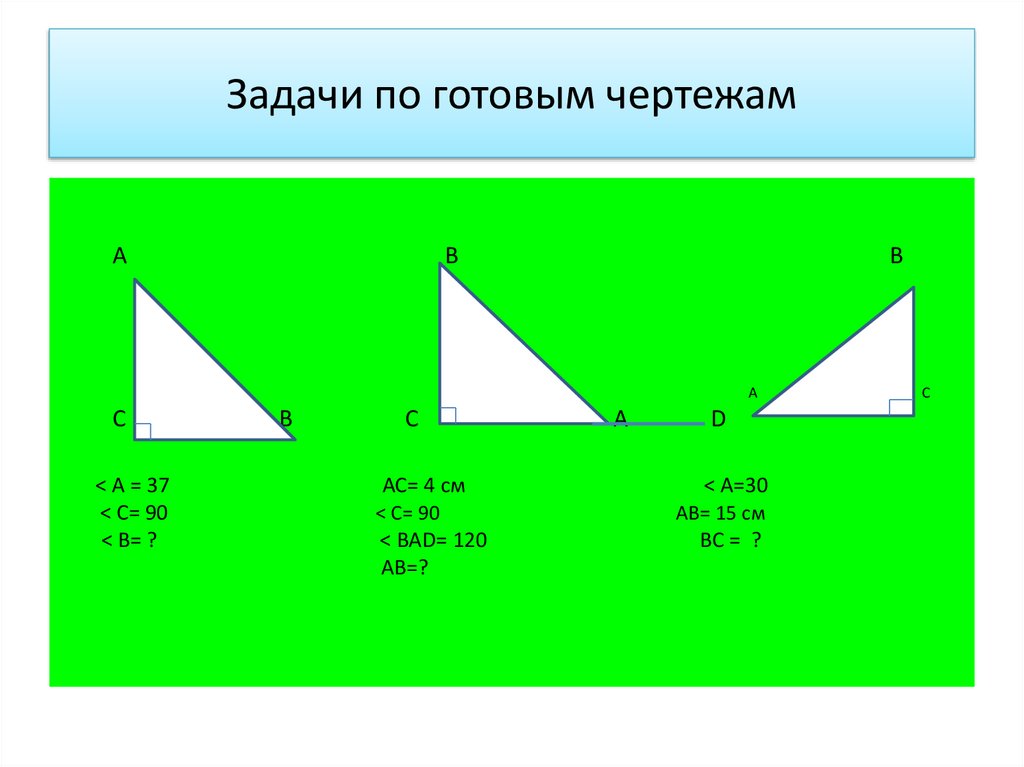
Как решать задачи на прямоугольные треугольники для учеников 7 класса: полезные рекомендации
На данной странице собраны полезные советы и изображения для выполнения задач на прямоугольный треугольник, которые могут встретиться в 7 классе. Здесь вы найдете подробные разъяснения, полезные формулы и примеры для успешного освоения этой темы. Все рекомендации помогут вам быстрее понять основные принципы и методы решения таких задач, а также научат правильно применять теоремы и свойства прямоугольных треугольников.

Для решения задач на прямоугольный треугольник важно помнить, что гипотенуза всегда противоположна прямому углу.

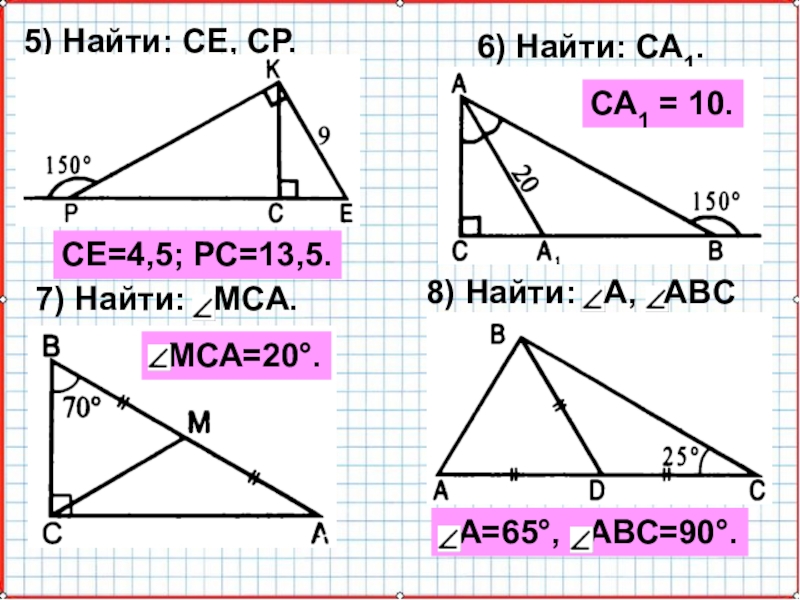
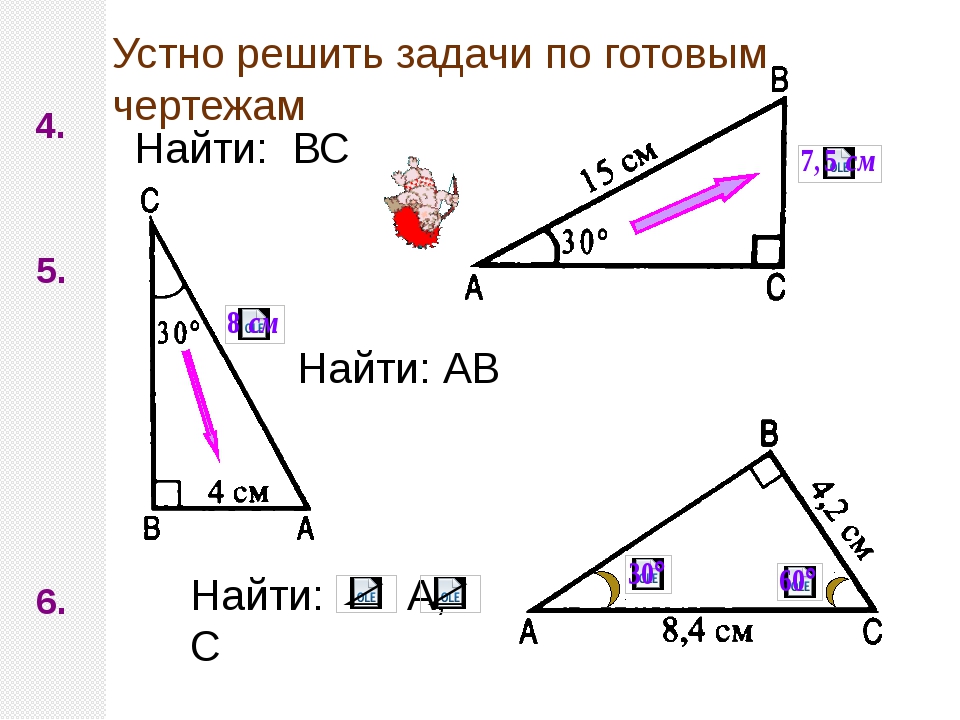
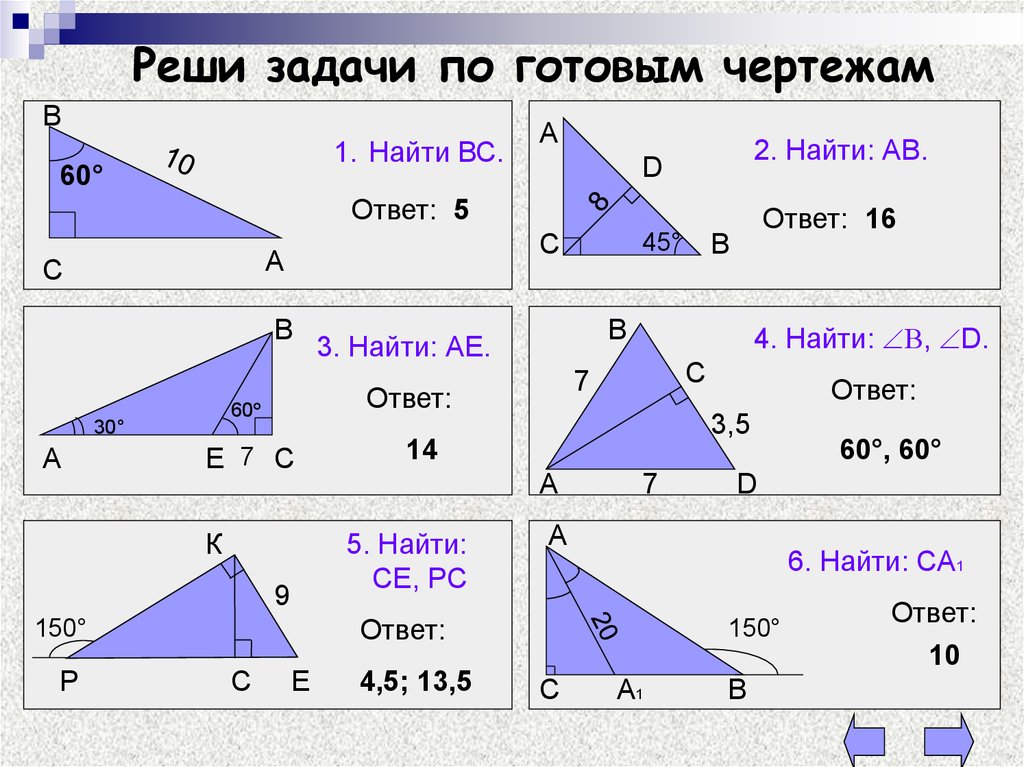
Геометрия 7 класс. Прямоугольные треугольники
Используйте теорему Пифагора для нахождения неизвестных сторон треугольника: а² + b² = c², где c – гипотенуза, а a и b – катеты.

Треугольники. 7 класс.
Обратите внимание на соотношение между углами прямоугольного треугольника: сумма двух острых углов всегда равна 90°.

Геометрия 7 класс : Решение задач \

Если одна из сторон треугольника известна, можно использовать пропорции для нахождения другой стороны, если известен угол.

Геометрия, 7 класс. Решение задач по теме \
Не забывайте, что в прямоугольных треугольниках могут быть использованы и другие теоремы, такие как теорема о медиане, делящей гипотенузу пополам.
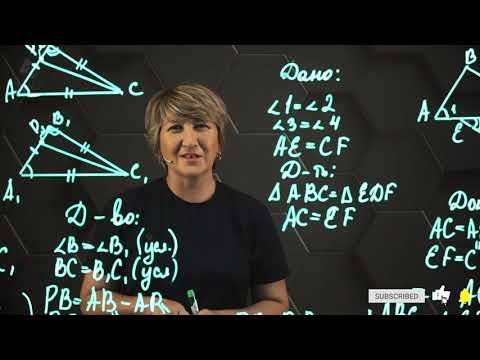
Признаки равенства треугольников. Практическая часть. 7 класс.

Обязательно рисуйте схему задачи, это поможет лучше понять взаимное расположение сторон и углов треугольника.
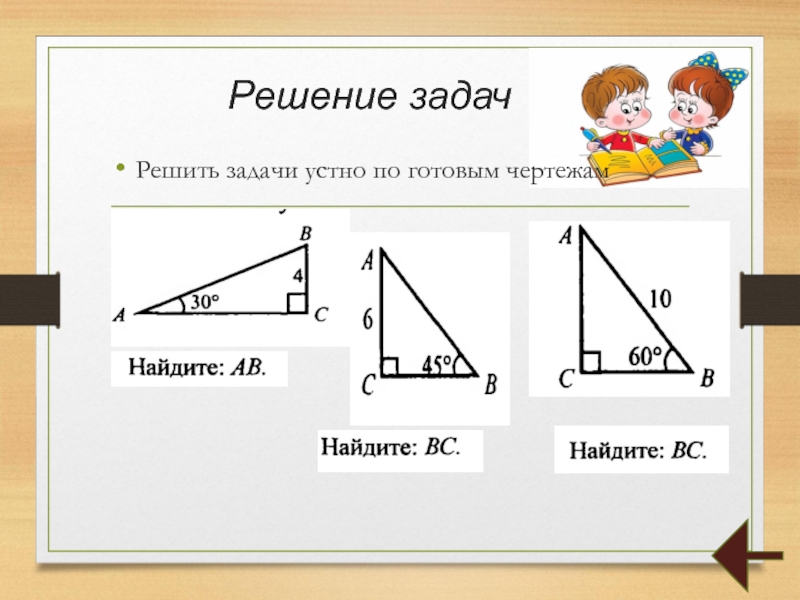
Применяйте формулу площади прямоугольного треугольника: S = 1/2 * a * b, где a и b – катеты.
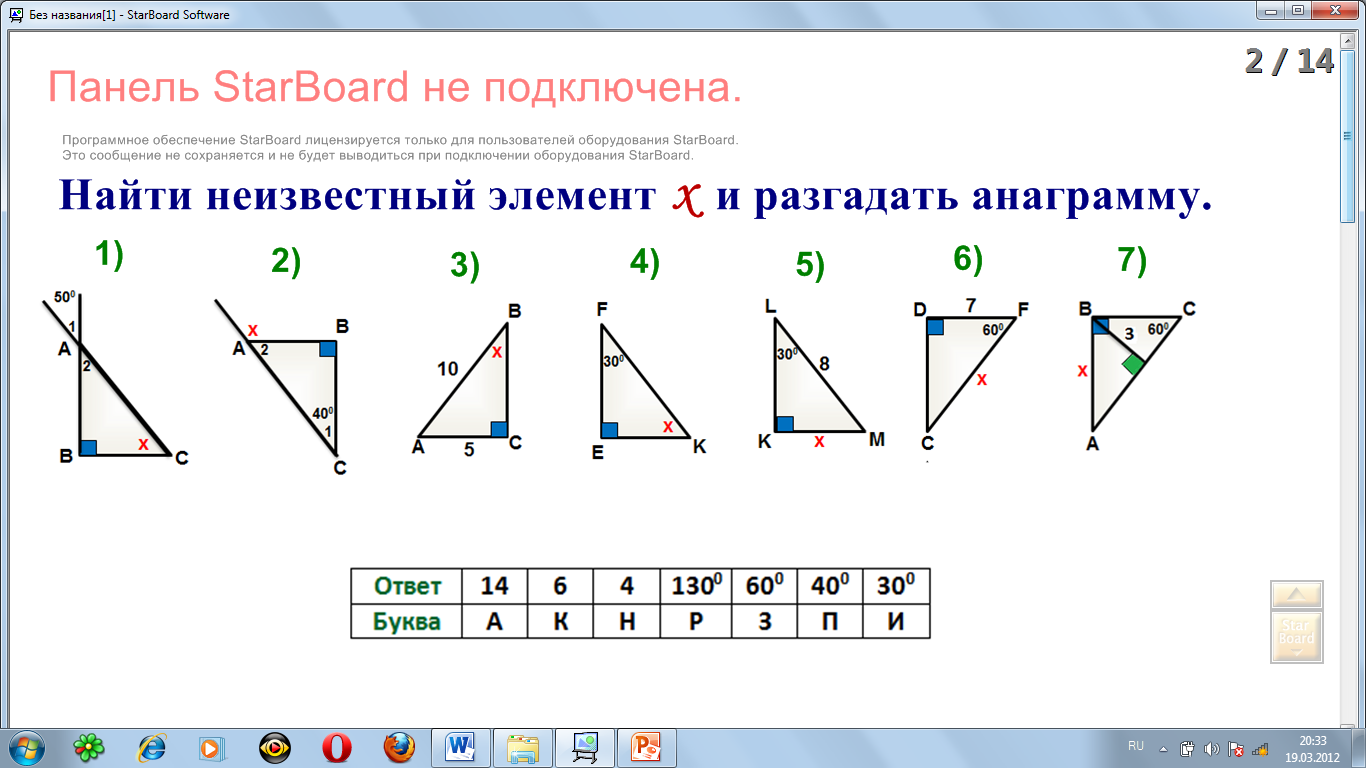
При решении задач с углами не забывайте о тригонометрических функциях: синус, косинус и тангенс, которые могут упростить вычисления.

Свойства прямоугольного треугольника. Практическая часть. 7 класс.
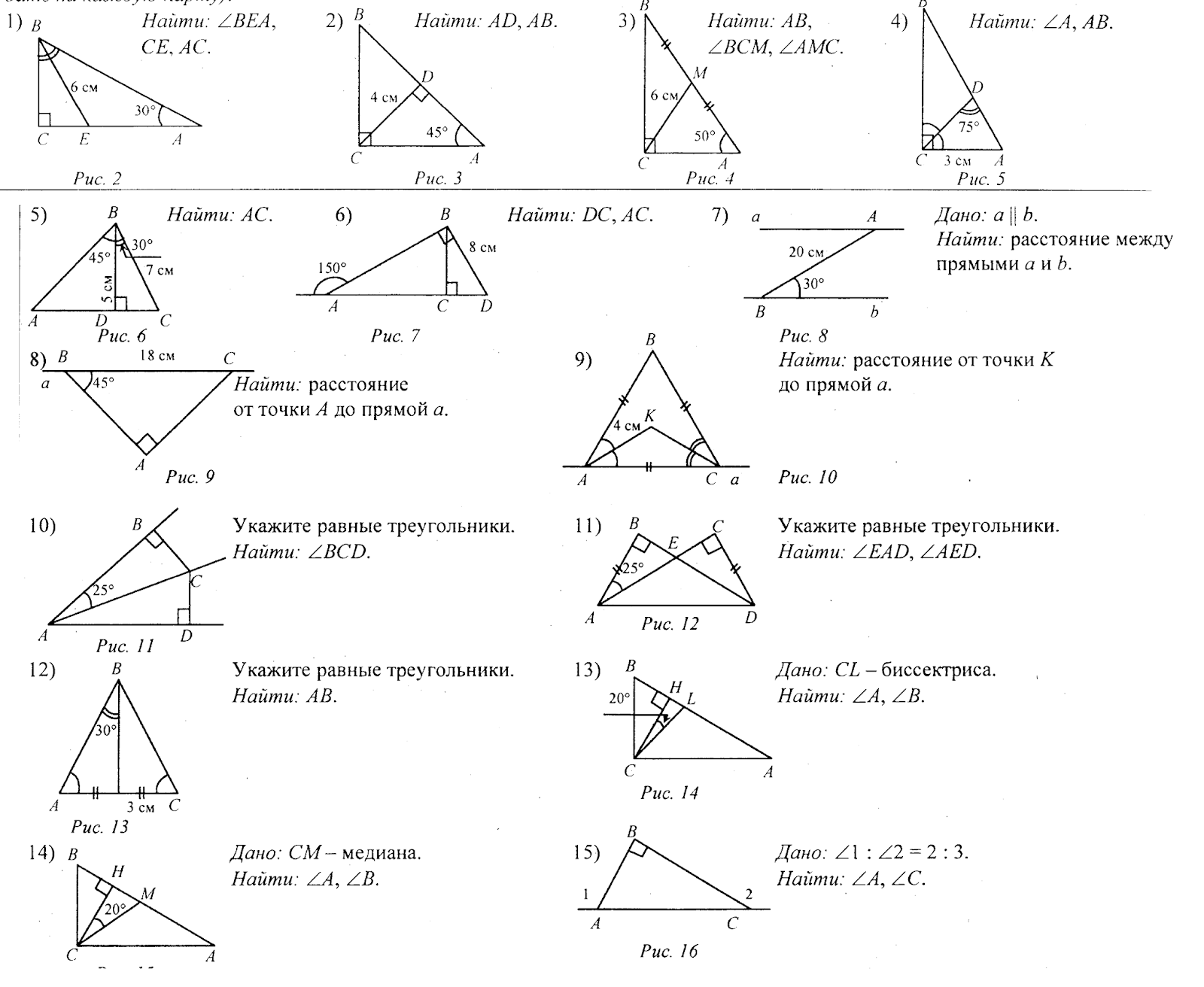
Если в задаче даны только углы, вы можете использовать таблицу значений тригонометрических функций для различных углов.


Регулярно тренируйтесь на примерах с различной степенью сложности, чтобы укрепить свои навыки в решении задач на прямоугольный треугольник.