Типы графов в теории алгоритмов и их практическое применение
Графы являются одним из ключевых понятий в теории алгоритмов и играют важную роль в решении множества задач, от поиска кратчайших путей до моделирования сложных сетевых структур. На этой странице мы рассмотрим различные виды графов, их характеристики и способы применения в алгоритмах. Понимание различных типов графов поможет улучшить алгоритмическое мышление и сделать решения более эффективными.
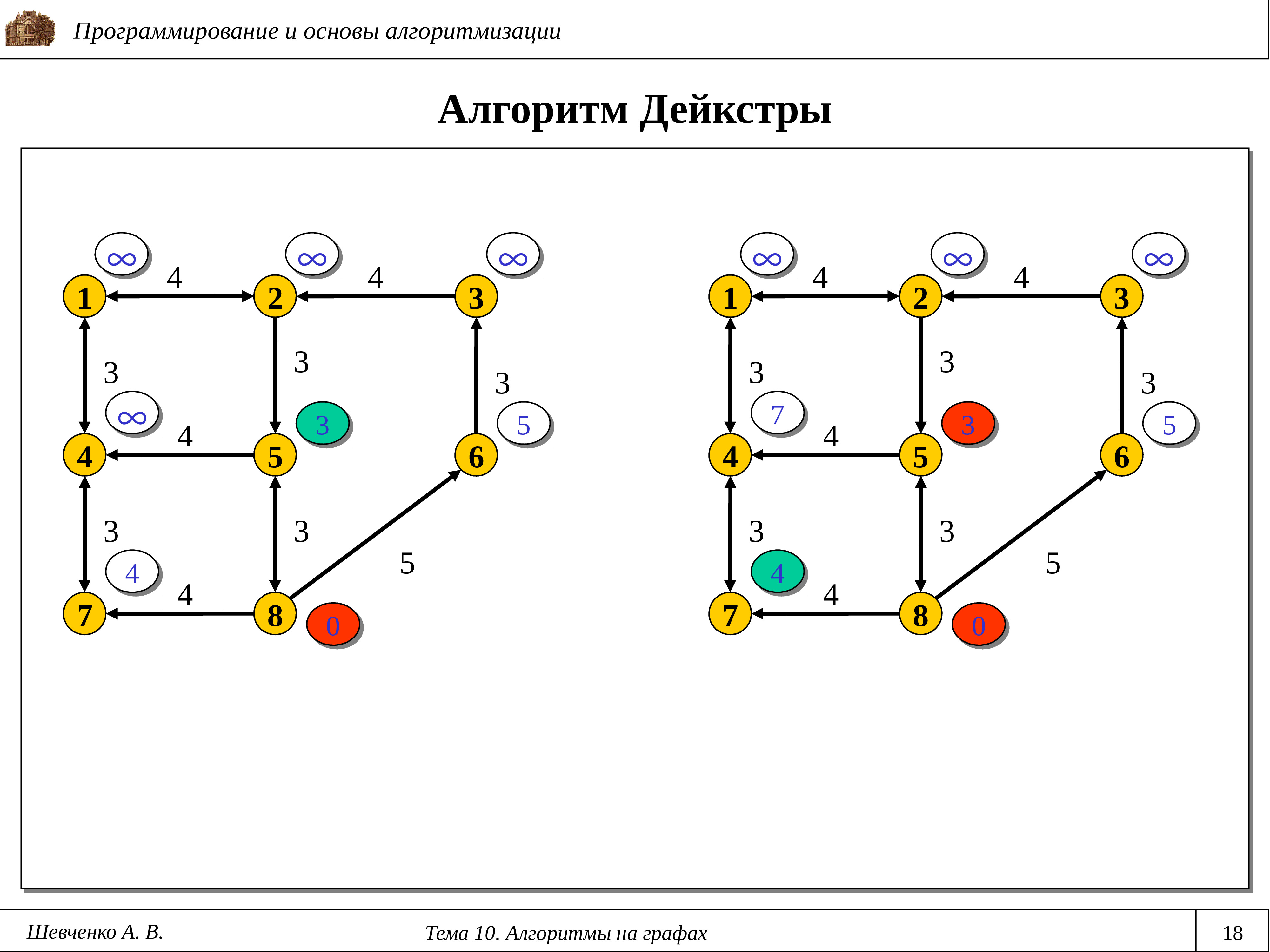
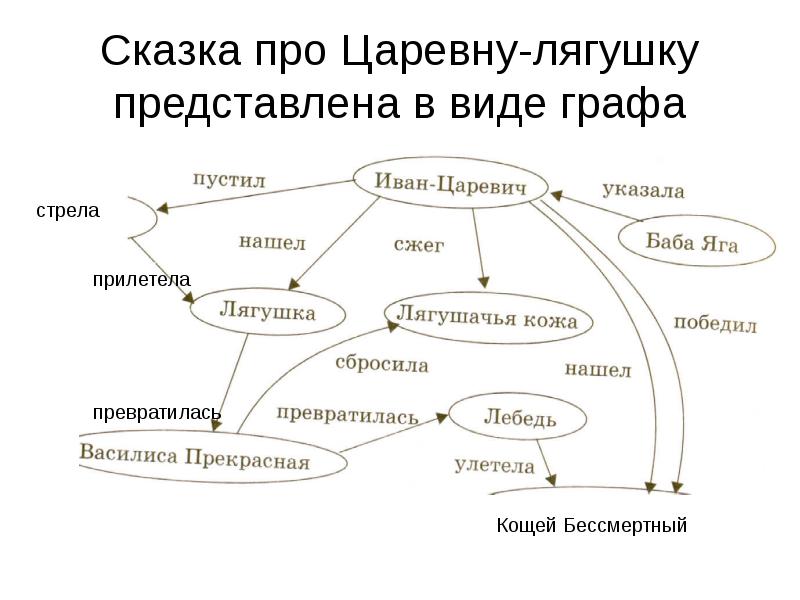
Перед тем как выбрать алгоритм для работы с графом, важно точно определить его тип: направленный или ненаправленный, взвешенный или невзвешенный.

Информатика Типы графов

Для поиска кратчайших путей лучше всего подходят графы с положительными весами, такие как графы с деревьями минимальных остовных или с алгоритмом Дейкстры.
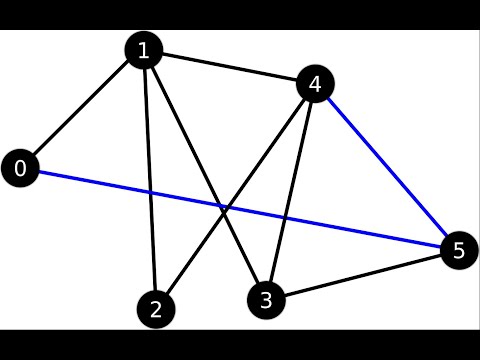
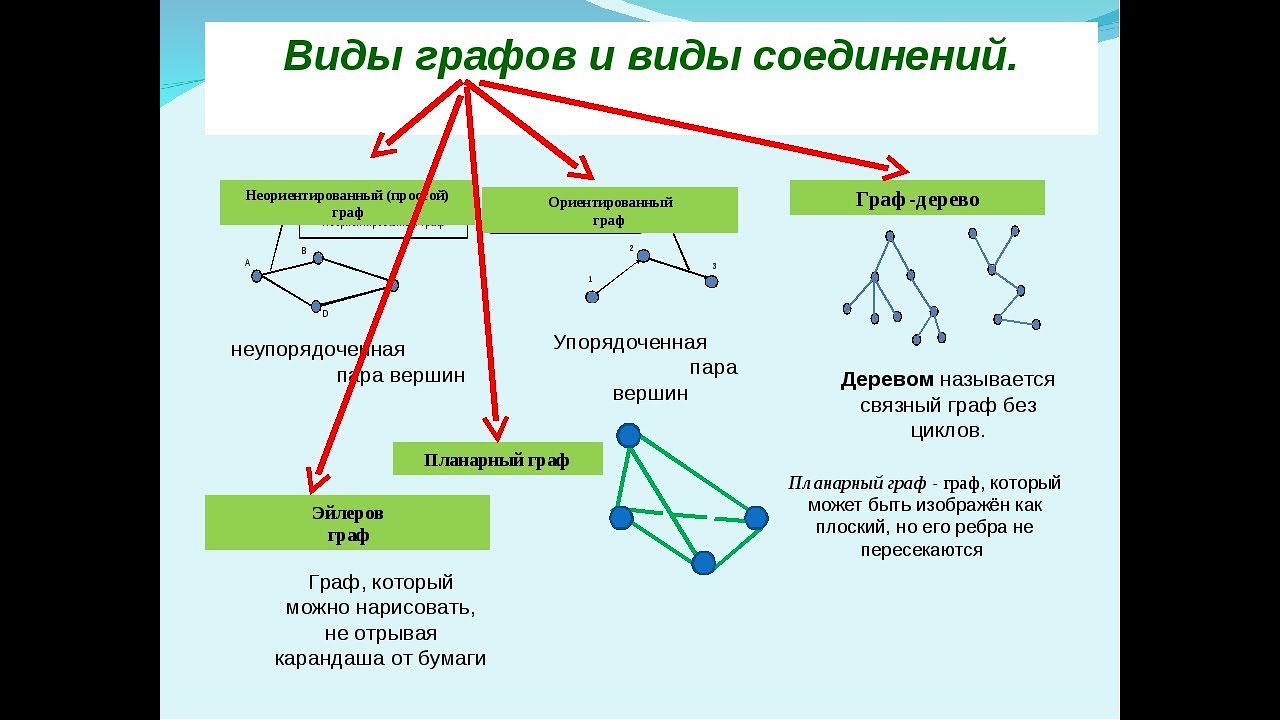
Виды графов
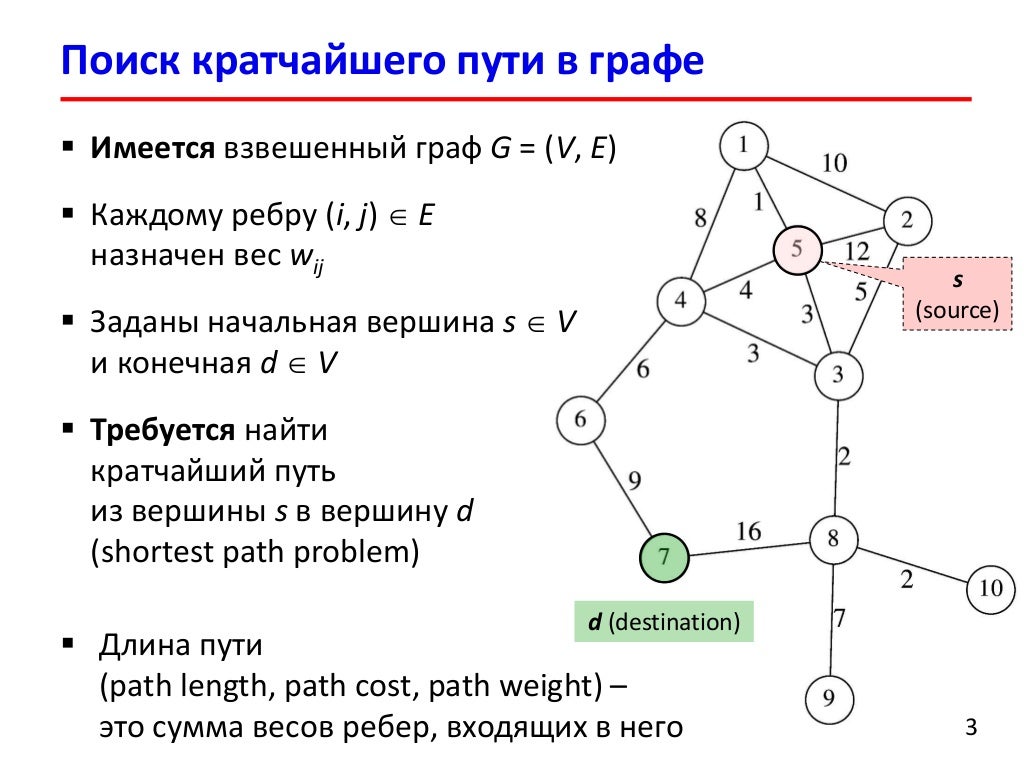
Использование ориентированных графов позволяет моделировать процессы, где важен порядок следования действий, например, в потоках данных или маршрутах доставки.

Информатика. Теория графов: Алгоритм поиска в ширину. Центр онлайн-обучения «Фоксфорд»
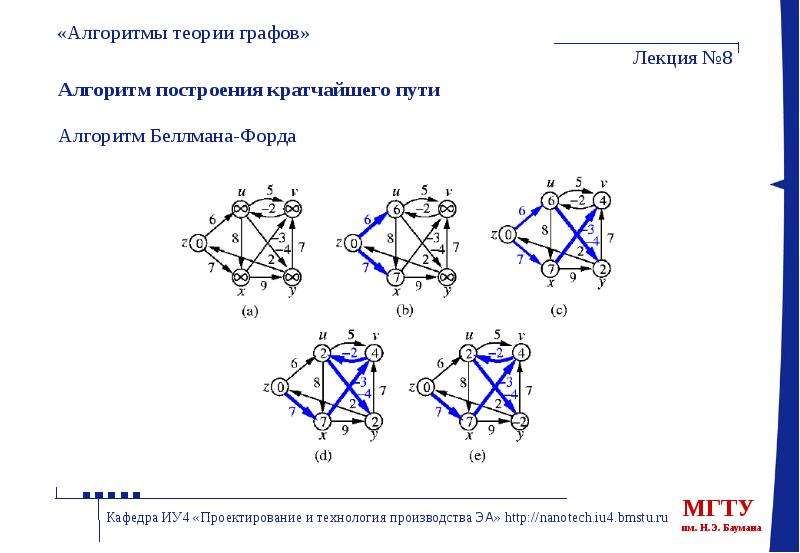
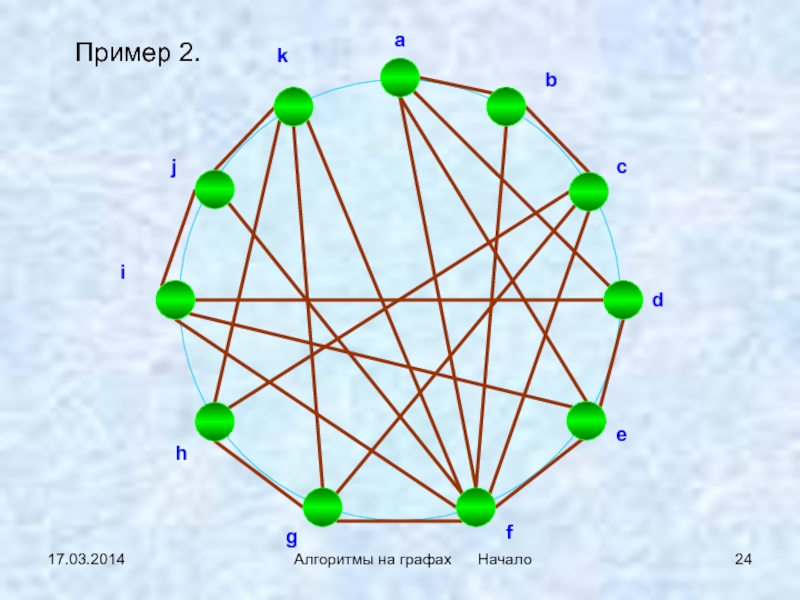
Взвешенные графы удобны для задач, где важна не только связь между вершинами, но и стоимость перехода между ними, как в задаче о минимальном остовном дереве.
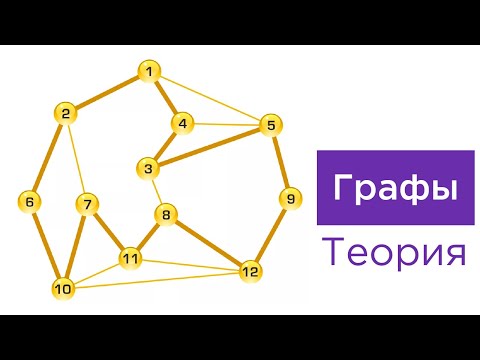
likerkacinema.ruение. Виды графов,степень вершин, ориентированный граф
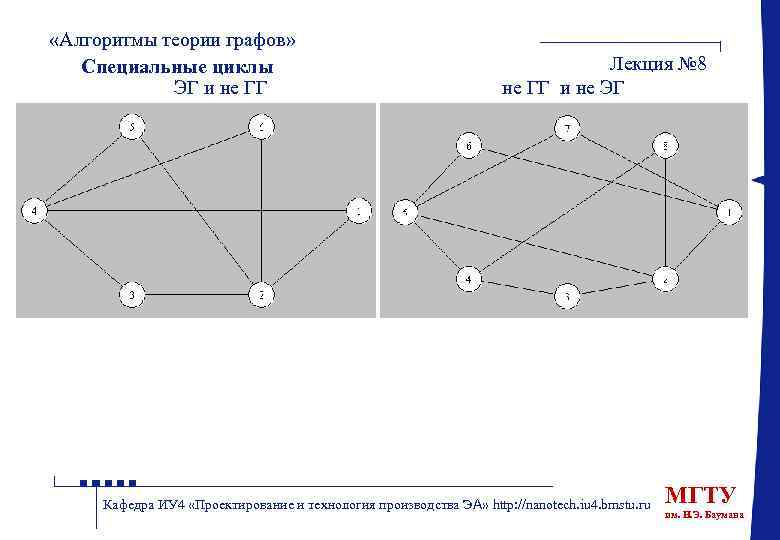
Циклические графы могут быть полезны для анализа повторяющихся процессов, таких как планирование задач с зависимостями или анализ социальных сетей.

КАК РАБОТАЮТ ГРАФЫ - СТРУКТУРЫ ДАННЫХ
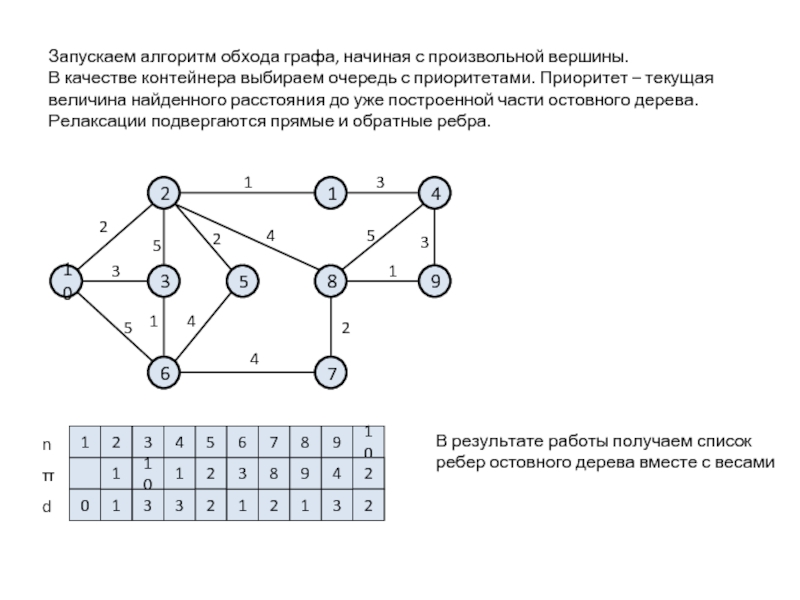
Графы без циклов (деревья) являются хорошим выбором для задач поиска и организации данных, где структура должна быть иерархической.

Если граф представляет собой сетку с множеством соединений, используйте алгоритмы поиска в глубину или ширину для эффективного обхода.

Методы и алгоритмы теории графов / ИТМО
Для сложных графов с множеством различных типов рёбер полезно использовать алгоритмы, которые поддерживают работу с метками или атрибутами рёбер и вершин.

Информатика, 10 класс Алгоритмы на графах Часть 1
Понимание различных типов графов поможет вам эффективно решать задачи маршрутизации, поиска путей и анализа сетевых структур, таких как интернет-трафик или логистика.
Используйте специальные структуры данных для представления графов, такие как матрицы смежности или списки смежности, в зависимости от плотности и типа графа.
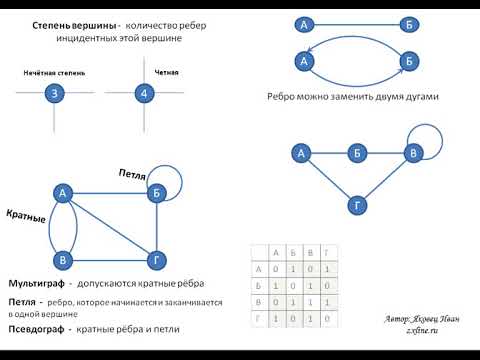
Графы, вершины, ребра, инцидентность, смежность