Пошаговое руководство по вычислению площади закрашенной фигуры в квадратных сантиметрах
Вычисление площади закрашенной фигуры может показаться сложным, но с правильным подходом и инструментами это становится гораздо проще. В данной статье мы рассмотрим основные способы, как точно и быстро вычислить площадь закрашенной фигуры в квадратных сантиметрах.
Для начала определите форму закрашенной фигуры — это может быть прямоугольник, круг или многоугольник. Правильное распознавание формы поможет выбрать подходящую формулу для расчета площади.

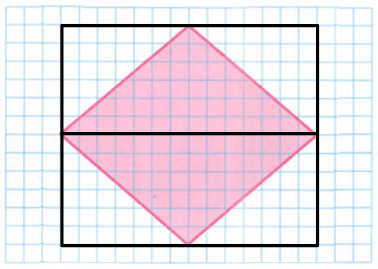
Площадь фигуры

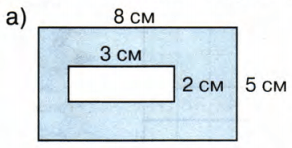
Если фигура состоит из нескольких простых элементов (например, прямоугольников и треугольников), разбейте её на такие части и вычисляйте площадь для каждой отдельно.

Как найти площадь фигуры?

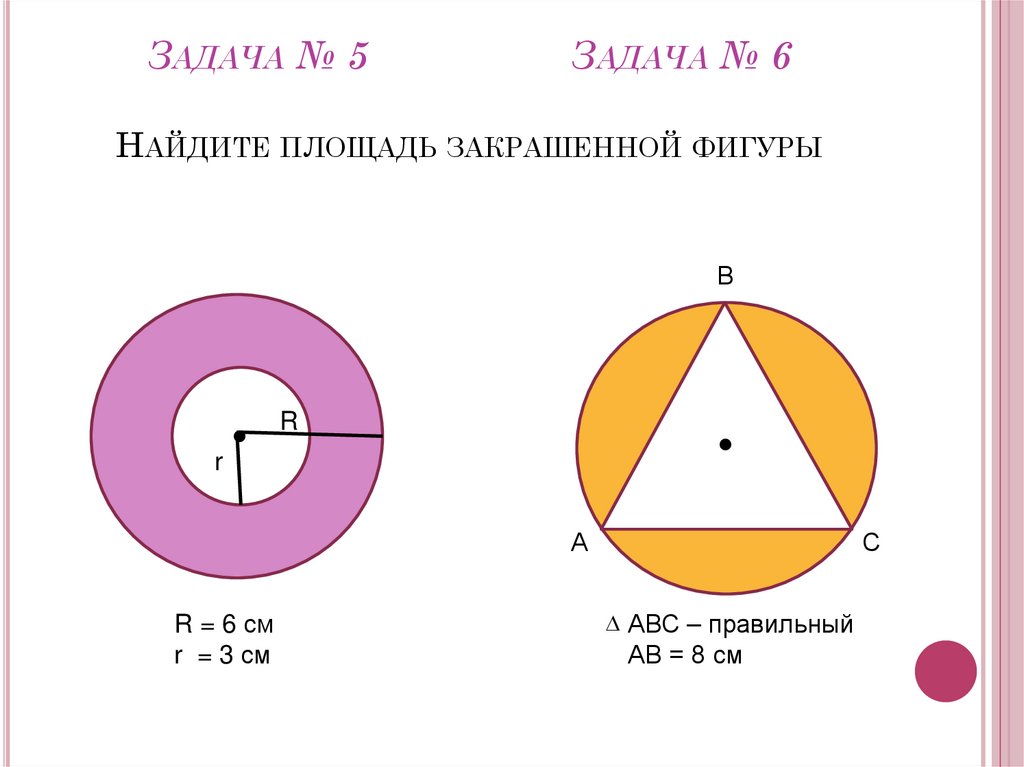
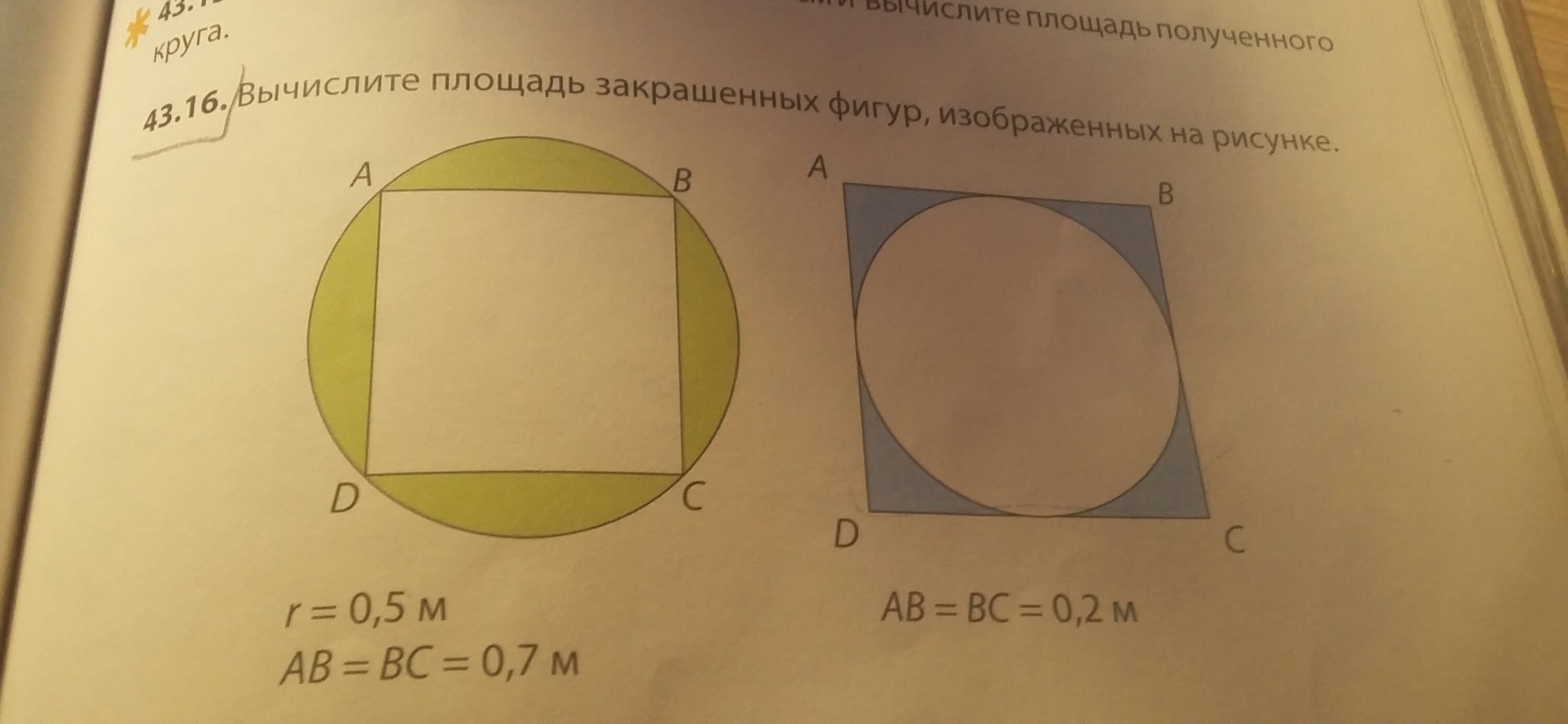
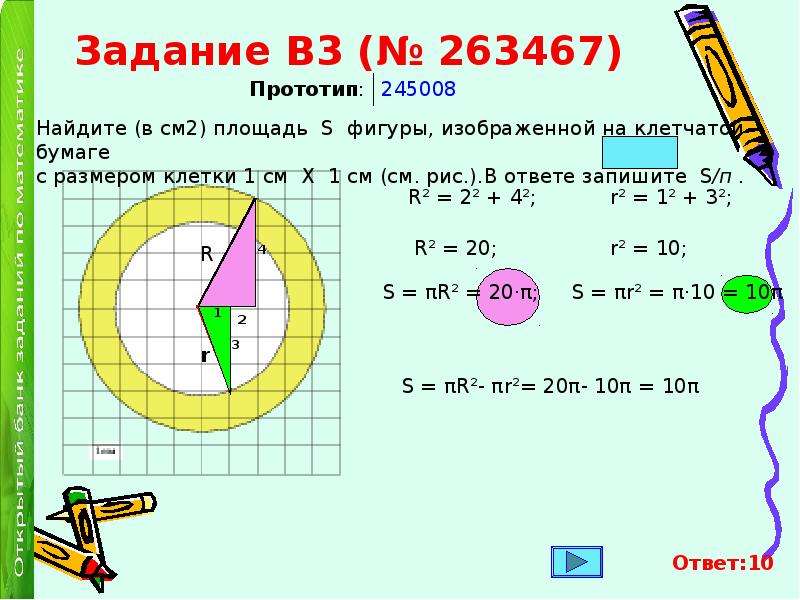
Для вычисления площади круга используйте формулу: площадь = π * r², где r — радиус круга.

Площадь квадрата. Как найти площадь квадрата?

Для прямоугольника площадь вычисляется по формуле: площадь = длина * ширина. Убедитесь, что измеряете стороны в сантиметрах, чтобы результат был в квадратных сантиметрах.

Найти площадь закрашенной фигуры

Если фигура сложная, и её невозможно разделить на простые геометрические фигуры, воспользуйтесь методом интегрирования, если это возможно.

Как найти площадь и периметр квадрата?

Не забывайте о единицах измерения: убедитесь, что все параметры в расчете даны в сантиметрах, иначе результат может быть ошибочным.
Используйте калькуляторы для сложных формул, чтобы не допустить ошибок при вычислениях.

Сингапурская головоломка Задача на логику
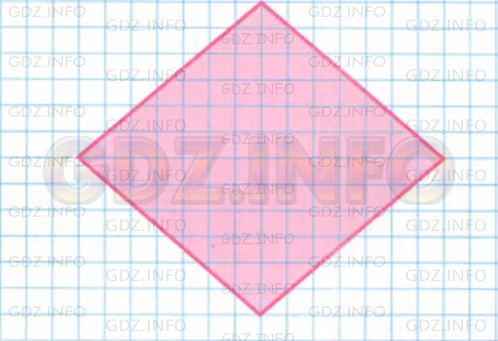
При работе с многоугольниками разбивайте их на треугольники, чтобы упростить расчеты площади.


Если фигура является сегментом круга, для вычисления площади используйте формулу площади сегмента: площадь = 0.5 * r² * (α - sin(α)), где α — угол сегмента в радианах.

Как найти площадь необычной фигуры? Математика

Если у вас есть доступ к цифровым инструментам, используйте программы или приложения для вычислений, такие как GeoGebra или другие геометрические калькуляторы.

Как найти площадь фигуры? - ВПР по математике в 4 классе - Задание №5