Как правильно применять условие интерполяции в решении математических и инженерных задач
Условие интерполяции является важным понятием, которое используется для точной оценки значений функции в точках, где она неизвестна, на основе уже имеющихся данных. Этот принцип активно применяется в математике, физике, инженерии и других дисциплинах. Важно правильно выбирать метод интерполяции, чтобы избежать ошибок и получить точные результаты при решении задач.
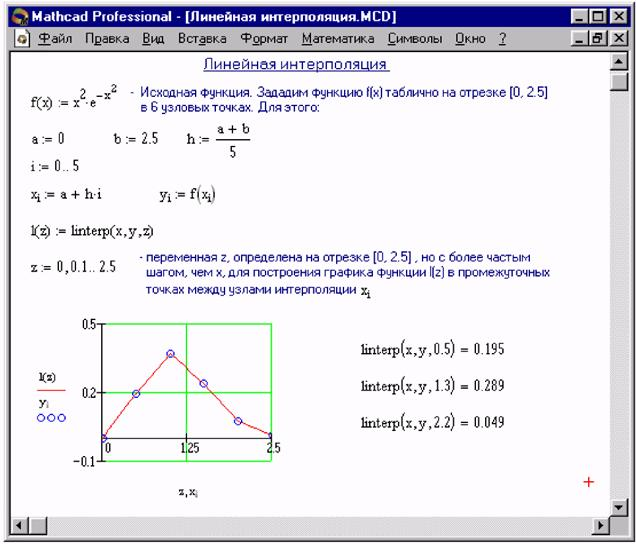
При применении условных интерполяций важно учитывать точность исходных данных для минимизации погрешностей.

Линейная интерполяция. Часть 2 (видео 38) - Пиксар


Не забывайте о выборе подходящего метода интерполяции в зависимости от типа задачи: линейная, полиномиальная или сплайновая интерполяция.

Лекция 8. Сходимость полиномиальной интерполяции. Сплайн-интерполяция.


Всегда проверяйте полученные результаты с помощью различных методов для подтверждения их точности.
Линейная интерполяция

Если данные неполные, рассмотрите возможность использования экстраполяции, однако будьте осторожны, так как она может привести к ошибкам.
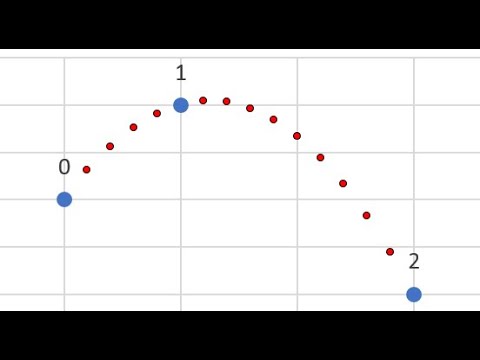
4.0 Линейная и квадратичная интерполяция
Для более сложных данных или при наличии выбросов используйте методы сглаживания, чтобы улучшить точность интерполяции.

Документы для иммиграции - Аргентина - Апостиль, перевод, легализация
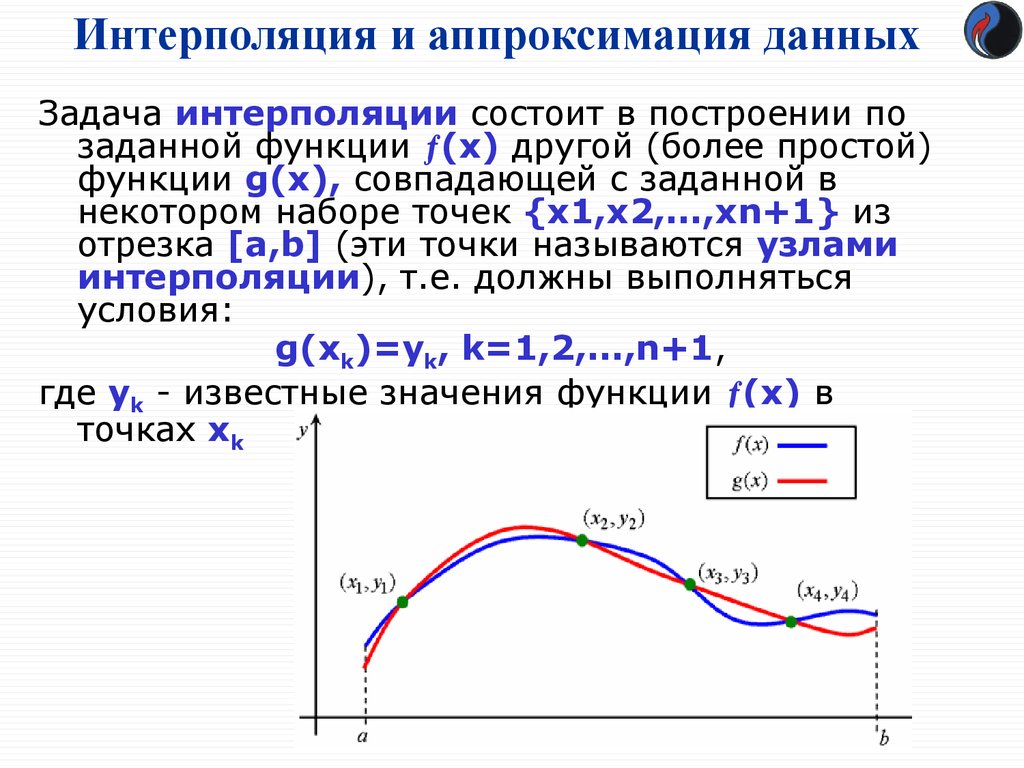
Регулярно проверяйте модель интерполяции на наличие ошибок и соответствие реальным данным.

Важно учитывать тип функции, которую вы пытаетесь интерполировать, чтобы выбрать наиболее подходящий метод.
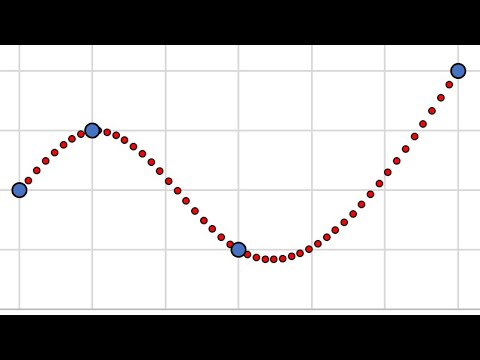
4.1 Интерполяция кубическими сплайнами

При работе с большими объемами данных используйте программное обеспечение, которое может автоматически выполнять интерполяцию.
Учитывайте вычислительные ограничения при выборе метода интерполяции, особенно для больших наборов данных.


Не забывайте о тестировании интерполированных данных для проверки их адекватности и реальности полученных результатов.
