Советы по расчету угла наклона вектора и его применению в научных исследованиях

Угол наклона вектора — это важная характеристика, которая используется в различных областях науки и техники. В этой статье мы рассмотрим, как правильно определить этот угол, как он влияет на физические процессы, и какие советы помогут вам эффективно работать с векторами в математике и физике.

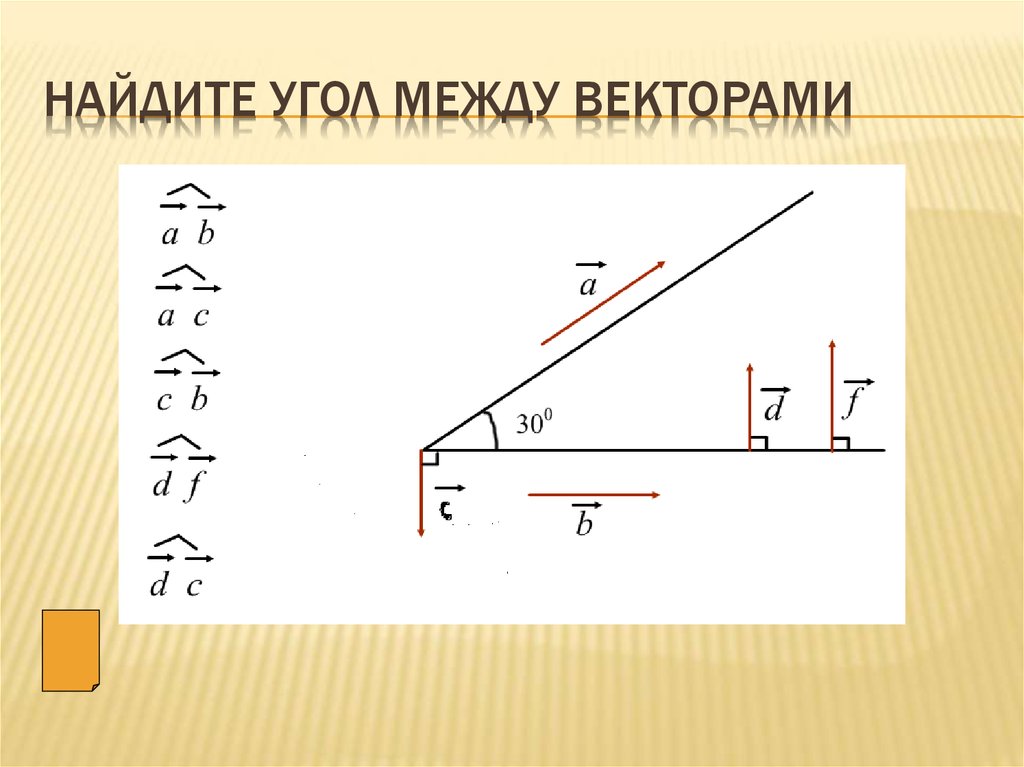
Для определения угла между двумя векторами используйте скалярное произведение, которое позволяет вычислить угол через косинус.

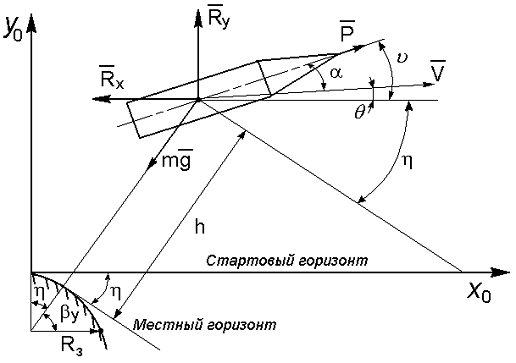
Запомните, что угол наклона вектора относительно горизонтальной оси можно вычислить через тангенс угла: tg(α) = y/x, где x и y — компоненты вектора.

Чтобы избежать ошибок, всегда проверяйте единицы измерения, особенно при работе с углами в разных системах координат.

В задачах механики угол наклона вектора часто используется для вычисления сил, действующих на объект, например, в задачах по наклону поверхности.

Не забывайте, что угол наклона вектора в трехмерном пространстве можно вычислять с помощью углов Эйлера или с использованием направления косинусов.

Если угол наклона важен для оптимизации, например, в машинном обучении, можно использовать производные для нахождения угла наклона градиента.

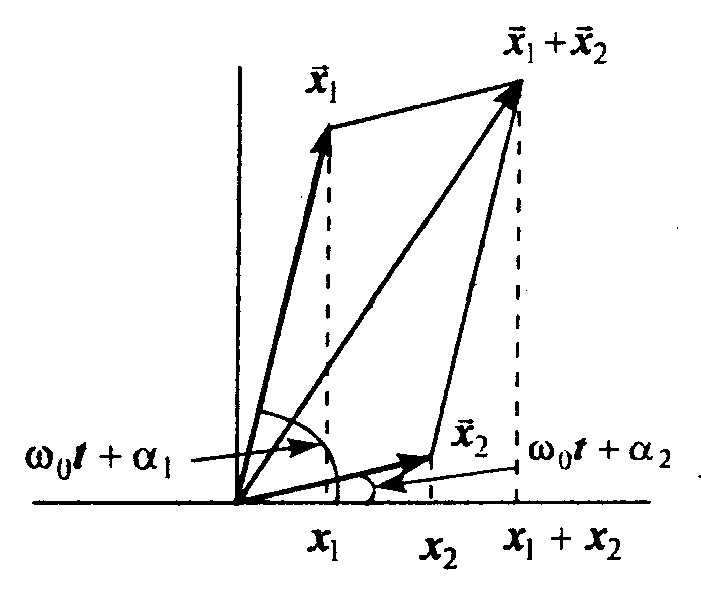
В задачах на движение углы наклона векторов часто определяют скорость и ускорение объекта в разных направлениях.

При работе с углом наклона вектора важно понимать, что изменение угла может существенно повлиять на направление и величину силы, действующей на объект.

Для более точных расчетов всегда уточняйте, о каком угле идет речь — об абсолютном или относительном к другим объектам.

Для векторов, заданных в полярной или цилиндрической системе координат, угол наклона вычисляется с использованием специфических формул, учитывающих особенности этих систем.