Центр тяжести простых геометрических фигур: формулы и полезные советы для точных расчетов
На этой странице собраны основные формулы для нахождения центра тяжести простых геометрических фигур, таких как треугольники, прямоугольники и круги. Вы найдете полезные советы, которые помогут вам правильно применять эти формулы в задачах и на практике.
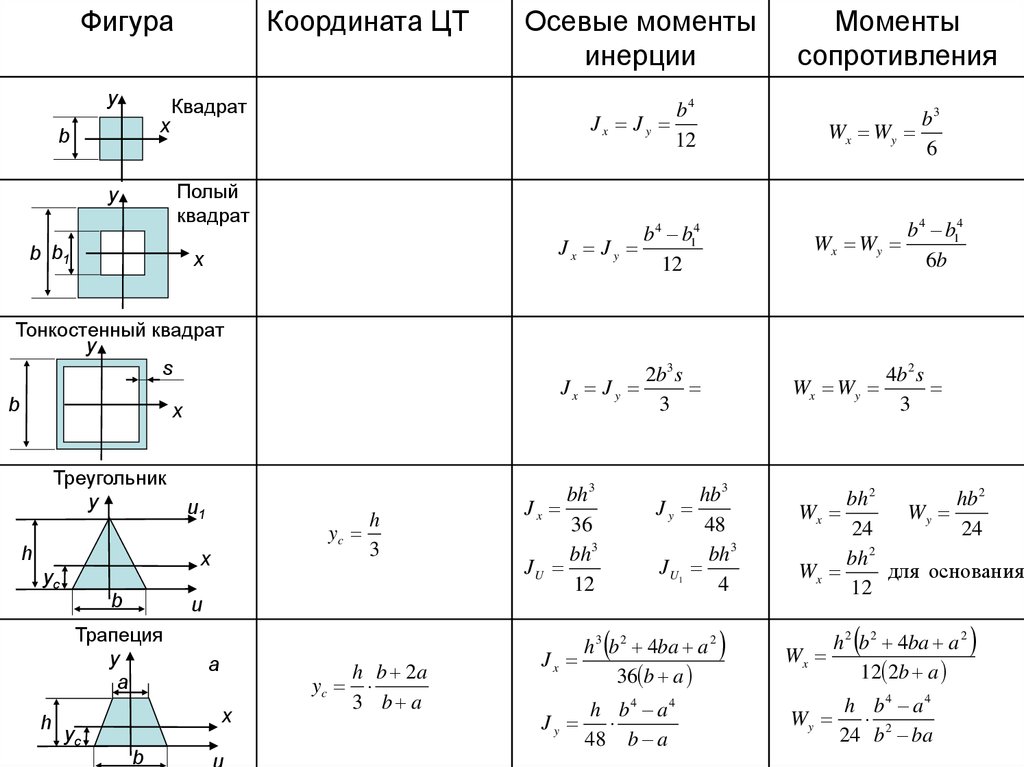
Для нахождения центра тяжести треугольника нужно воспользоваться формулой, где его координаты равны среднему значению координат вершин. Это позволяет быстро вычислить центр для любого треугольника.

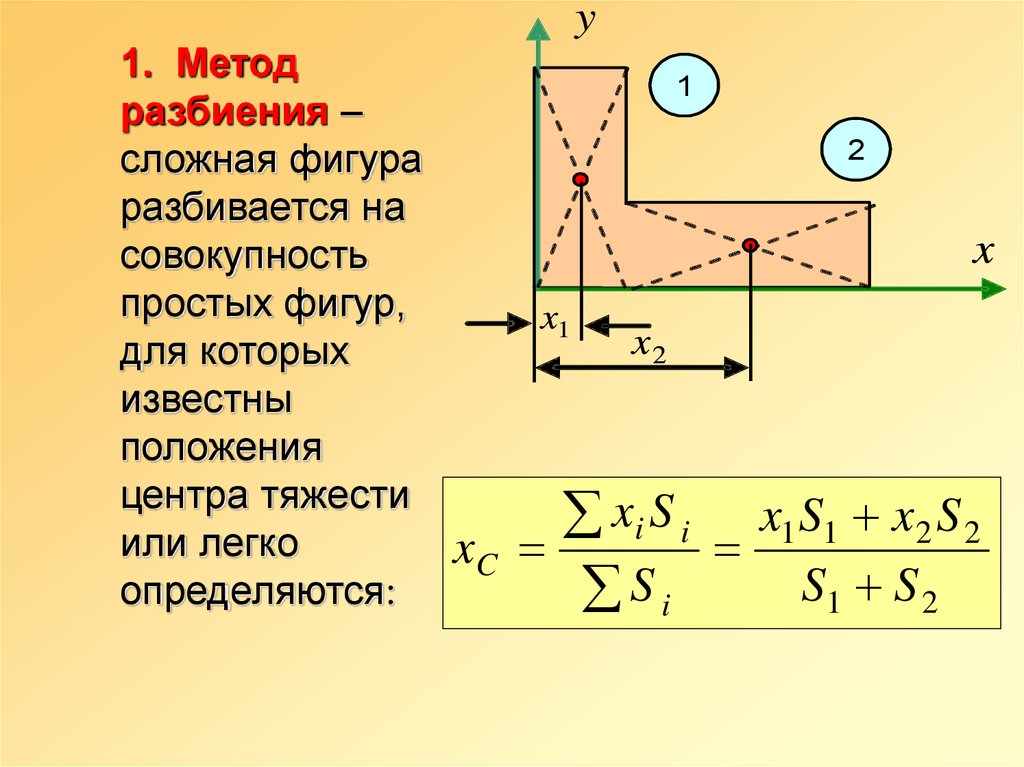
Определение центра тяжести сложной фигуры. Сопромат.
При расчете центра тяжести прямоугольника важно помнить, что его центр всегда будет находиться в точке пересечения диагоналей.

Определение центра тяжести сложной фигуры. Сопромат

Центр тяжести круга всегда совпадает с его центром, что делает расчеты для круговых фигур крайне простыми.

Самый короткий тест на интеллект Задача Массачусетского профессора
Для правильных расчетов всегда следите за единицами измерения — они должны быть одинаковыми для всех компонентов, чтобы избежать ошибок в вычислениях.

Центр тяжести тела. Условия равновесия тел - Физика 7 класс #46 - Инфоурок

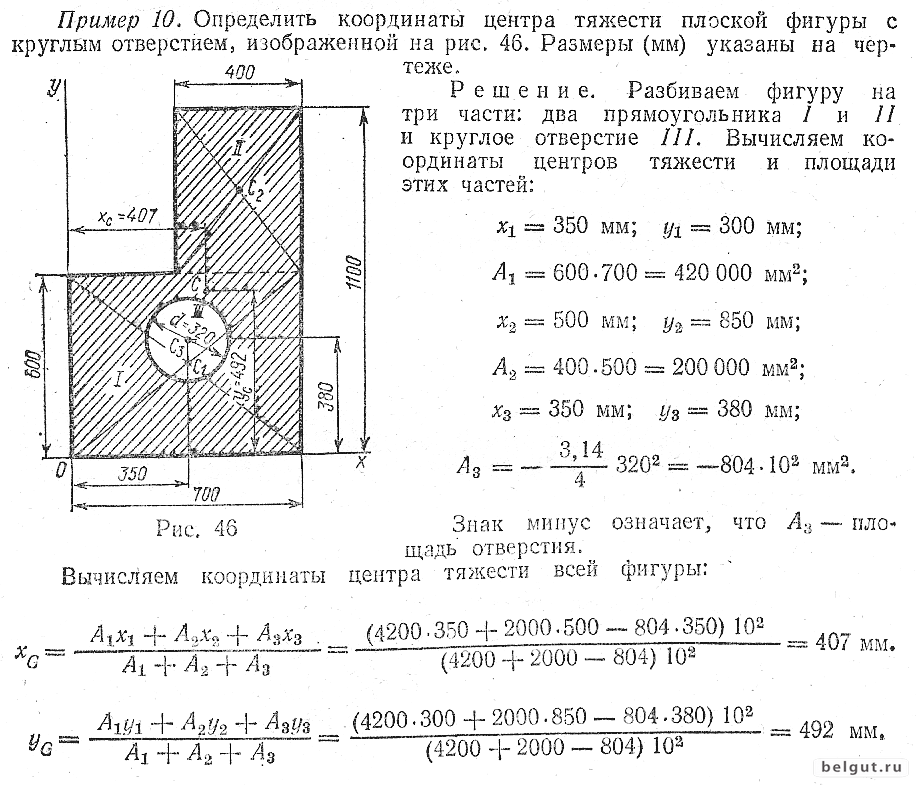
Вычисление центра тяжести сложных фигур можно разбить на несколько этапов, разделив фигуру на более простые части и найдя центры тяжести каждой из них.

Найдите центр тяжести

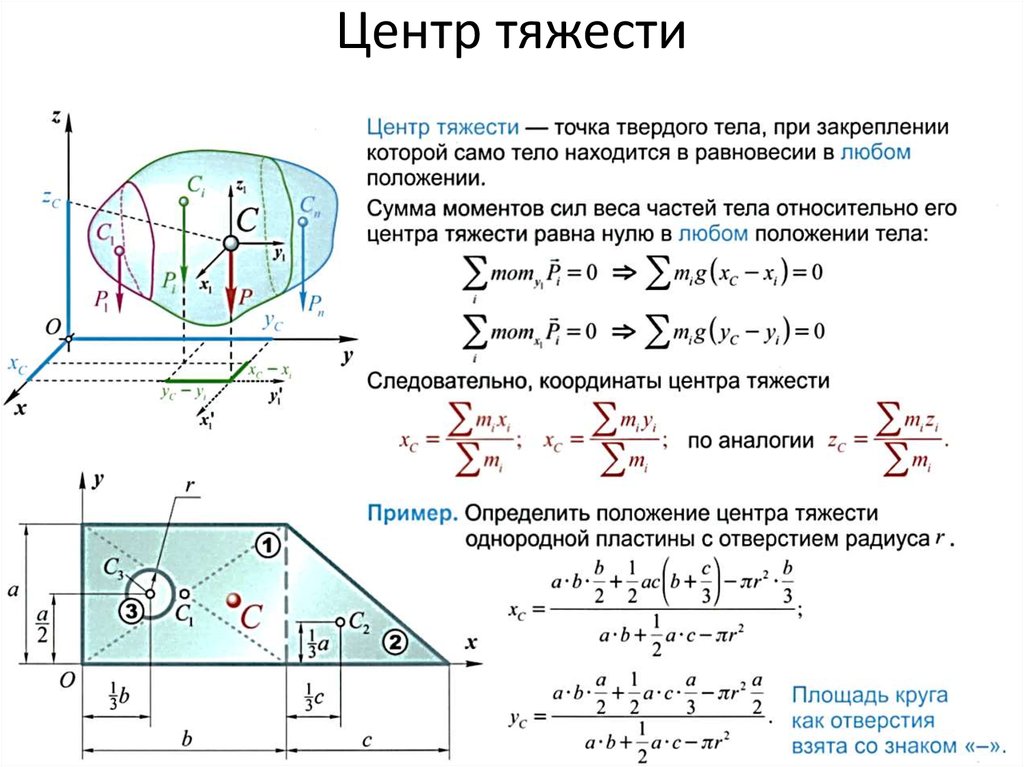
Для использования формул важно понимать, что центр тяжести объекта можно рассматривать как точку, в которой действует равнодействующая сила тяжести всего объекта.
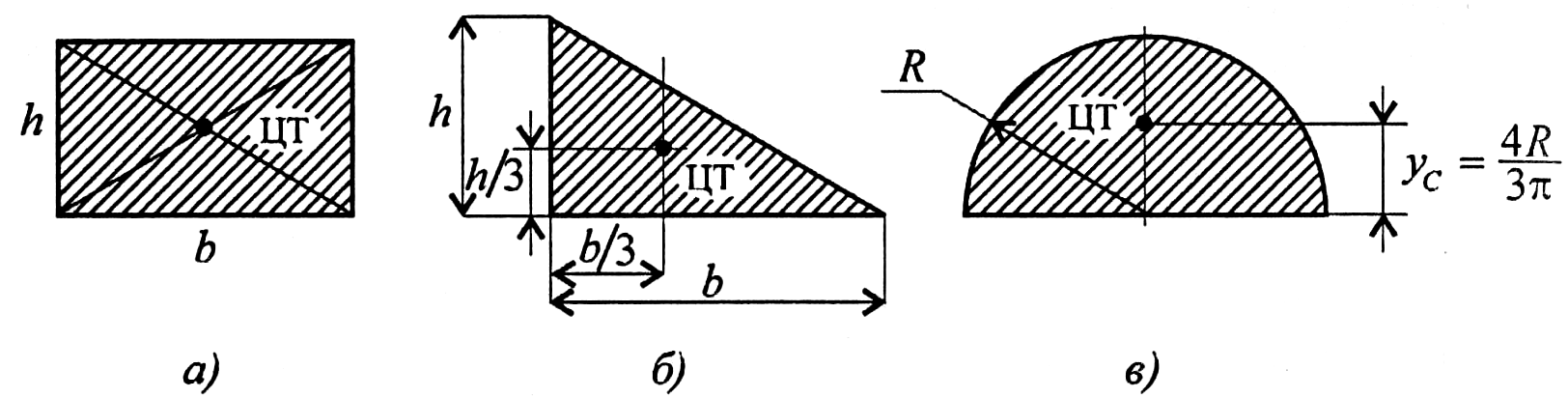
При вычислении центра тяжести симметричных фигур можно воспользоваться их симметрией, что значительно упрощает задачу.

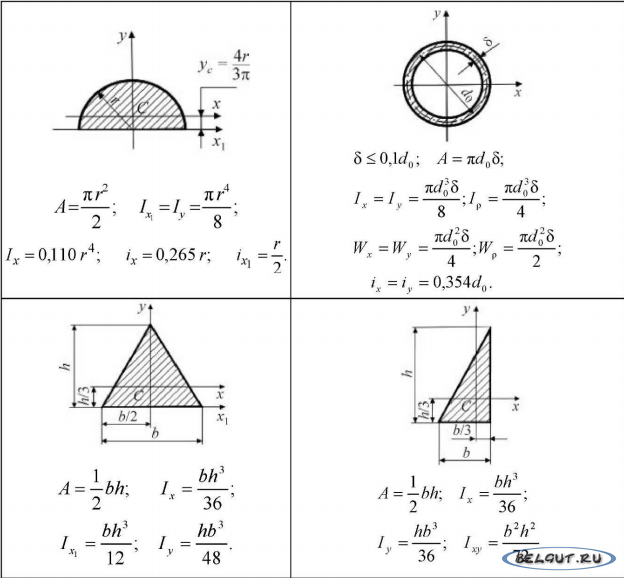
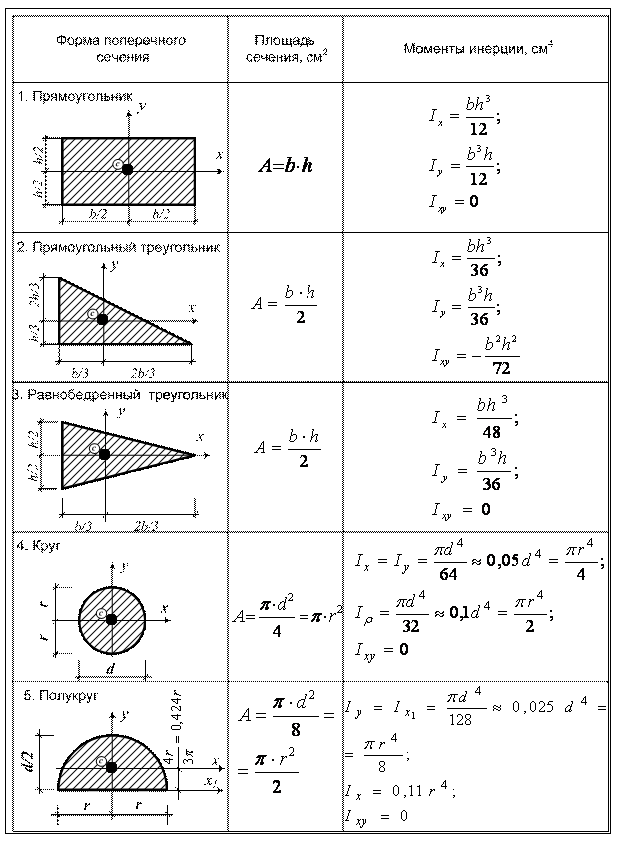
Определение центра тяжести сложных сечений. Фигуры из ГОСТ.
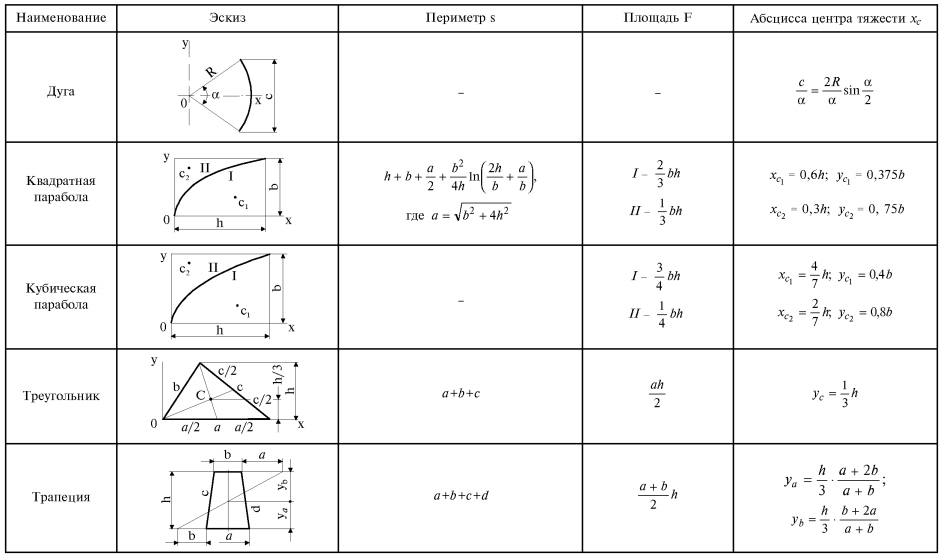
Используйте интегралы, если вам нужно найти центр тяжести фигуры сложной формы. Это может быть полезно для более точных вычислений.

Определение координат центра тяжести сложной фигуры (плоского сечения)


При работе с фигурами с постоянной плотностью можно использовать средние значения массы и площади для упрощения расчетов.

Определение центра тяжести плоской фигуры. Подробное объяснение. Сопромат для чайников

Если фигура имеет неравномерную плотность, необходимо учитывать распределение массы по всему объекту, что усложнит вычисления, но сделает их более точными.

Практическая №5 Определение центра тяжести сложной фигуры
Тайна числа 1.618034. или как НЕЧТО генерирует ЧТО-ТО.