Как правильно сформулировать целевую функцию транспортной задачи для эффективного решения логистических проблем
Целевая функция транспортной задачи играет ключевую роль в нахождении оптимальных путей транспортировки ресурсов с минимальными затратами. Этот элемент линейного программирования позволяет эффективно решать задачи, связанные с распределением товаров или услуг между различными точками, учитывая стоимость перевозки, ограничения на количество ресурсов и другие параметры. Важно понимать, как правильно ее сформулировать и оптимизировать для достижения наилучших результатов.


При формулировке целевой функции транспортной задачи учитывайте все возможные ограничения, такие как объемы поставок и потребностей, чтобы точно отразить реальную ситуацию.

Транспортная задача для чайников по шагам за 15 минут. Применение транспортной задачи в экономике


Не забывайте о том, что целевая функция должна быть линейной, что значительно упрощает использование стандартных методов оптимизации, таких как метод северо-западного угла или метод потенциалов.
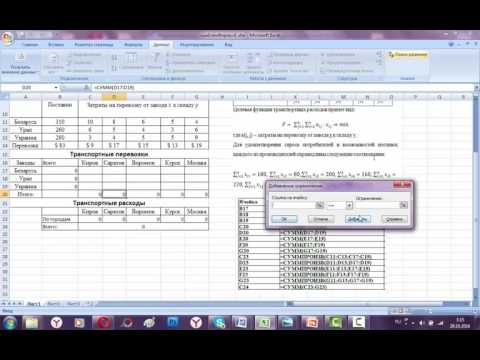
Транспортная задача


Внимательно проверяйте все исходные данные и исходные условия задачи, так как даже небольшие ошибки могут повлиять на точность решения целевой функции.
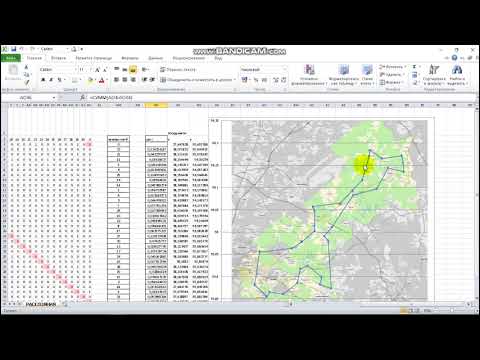
Решение транспортной задачи с помощью Anylogic.

Если транспортная задача включает большое количество пунктов, попробуйте использовать программные средства для вычислений, чтобы избежать трудоемких ручных расчетов.

Тема 8. Транспортная задача
При работе с транспортной задачей важно учитывать возможные изменения в условиях, такие как колебания стоимости перевозок или изменение объемов поставок, чтобы своевременно подкорректировать модель.
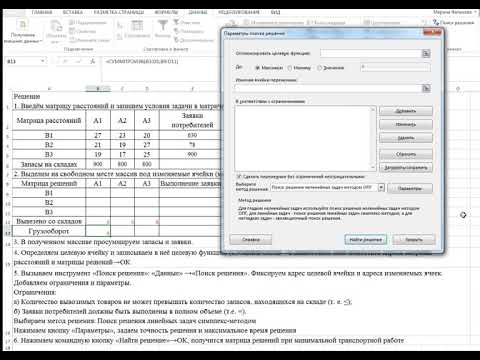
Видео урок по АЛО Пример решения транспортной задачи


Метод минимальных затрат — это один из наиболее эффективных способов решения транспортной задачи, при котором минимизируются общие затраты на транспортировку.

Обратите внимание на то, как расположены источники и потребители в транспортной задаче: для оптимизации затрат важно правильно распределить ресурсы и маршруты.
Не забывайте, что целевая функция должна быть адаптирована под конкретные условия задачи, включая возможные дополнительные ограничения, такие как сроки доставки или специфические требования к транспорту.

Для решения транспортной задачи можно использовать различные методы оптимизации, такие как симплекс-метод или метод потенциалов, в зависимости от сложности задачи.

Транспортная задача

Решение транспортной задачи требует четкого понимания математических принципов линейного программирования, что позволяет точнее формулировать и оптимизировать целевую функцию.