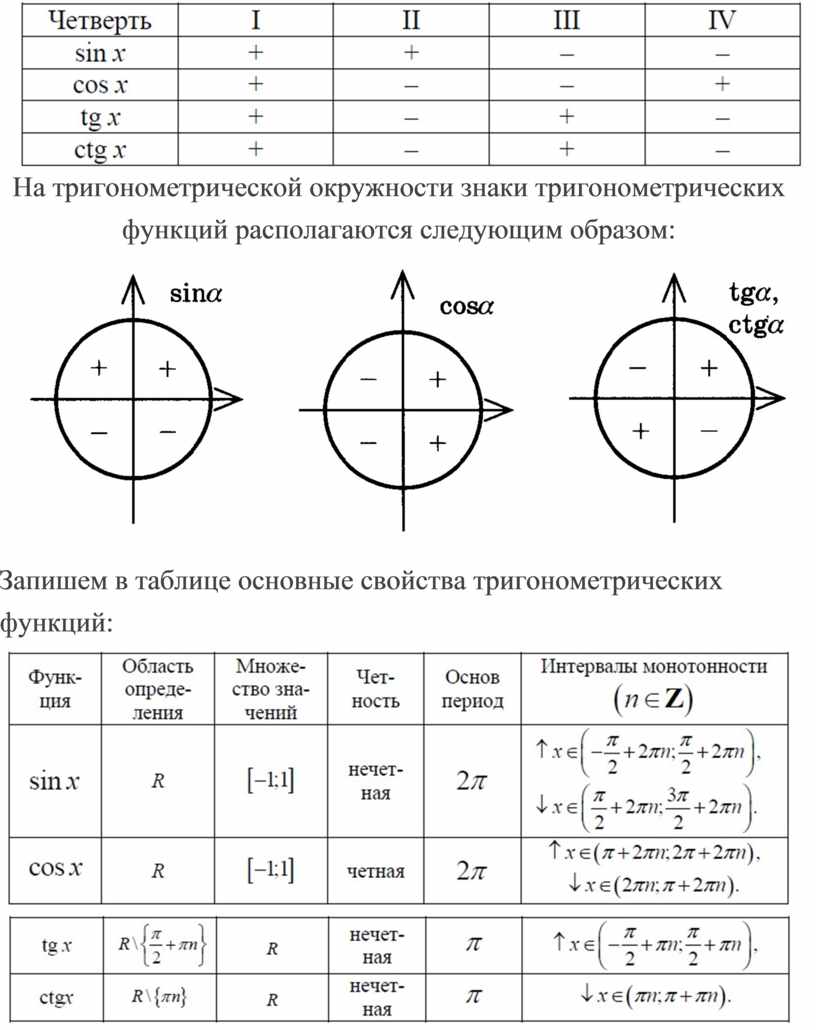
Тригонометрический круг и таблица синусов: подробный обзор и полезные советы

На этой странице собраны полезные советы и таблица синусов, которые помогут вам лучше понять тригонометрический круг и его применение в математике. Вы найдете практические рекомендации, которые облегчат процесс обучения и помогут быстрее запомнить ключевые значения.

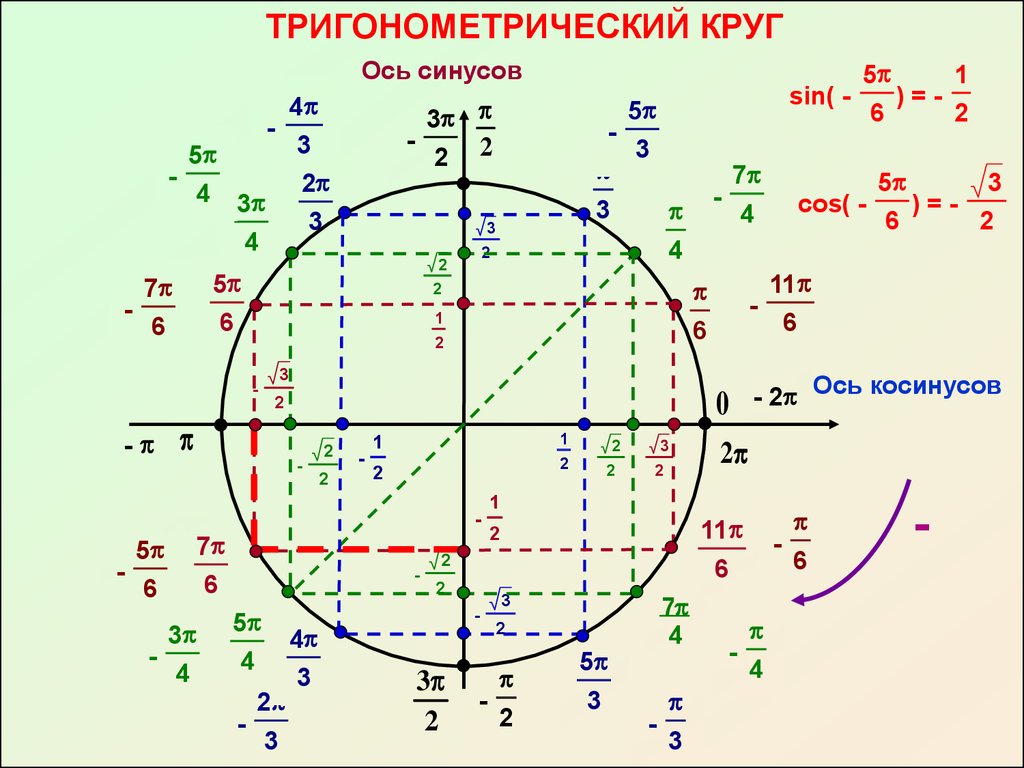
Для запоминания значений синусов и косинусов углов используйте симметричные свойства тригонометрического круга, такие как четность и нечетность функций.

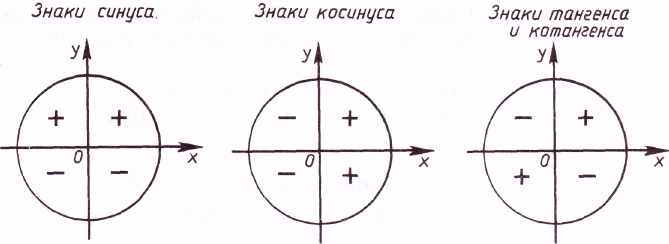
Учите значения синусов и косинусов для углов, кратных 30°, 45° и 60° — они часто встречаются на экзаменах и в заданиях.

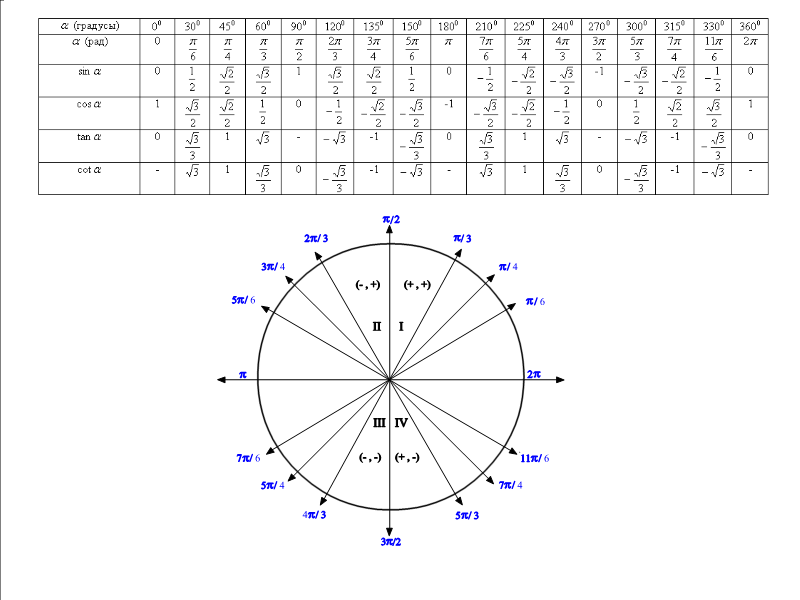
Запомните, что синус угла равен косинусу его дополняющего угла (90° - угол) для углов, меньших 90°.

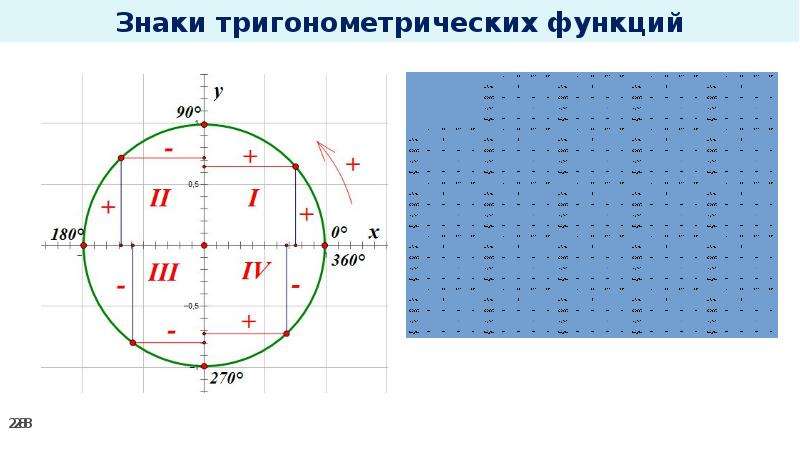
Используйте тригонометрический круг для визуализации значений синуса и косинуса для различных углов, чтобы легче запоминать их.

Старайтесь решать задачи с использованием тригонометрических функций на практике, это поможет вам быстрее освоить таблицу синусов и других функций.

Помимо таблицы синусов, изучайте и другие тригонометрические функции — такие как тангенс и котангенс, — это важно для комплексного понимания темы.

Понимание тригонометрического круга поможет вам в решении сложных геометрических и физико-математических задач.

Используйте онлайн калькуляторы и графики для практики и быстрого сверки значений тригонометрических функций, это сэкономит время и повысит точность.

Не забывайте о периодичности тригонометрических функций: синус и косинус имеют период 360°, а тангенс — 180°.

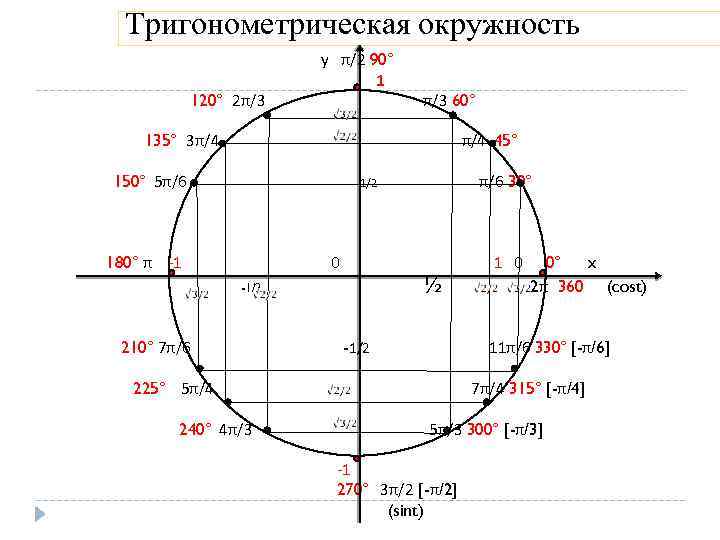
Для углов, превышающих 360°, возвращайтесь к углам, выраженным в пределах одного оборота (0°–360°), используя принцип периодичности функций.