Понимание геометрии треугольника с углами 40° и 70°: важные аспекты
Равнобедренный треугольник с углами 40° и 70° — интересная геометрическая фигура, которая может встречаться в различных задачах. Важно понимать его свойства для точного решения задач в области геометрии, архитектуры и других дисциплин. Эта страница содержит полезные советы и изображения, которые помогут разобраться в особенностях такого треугольника.
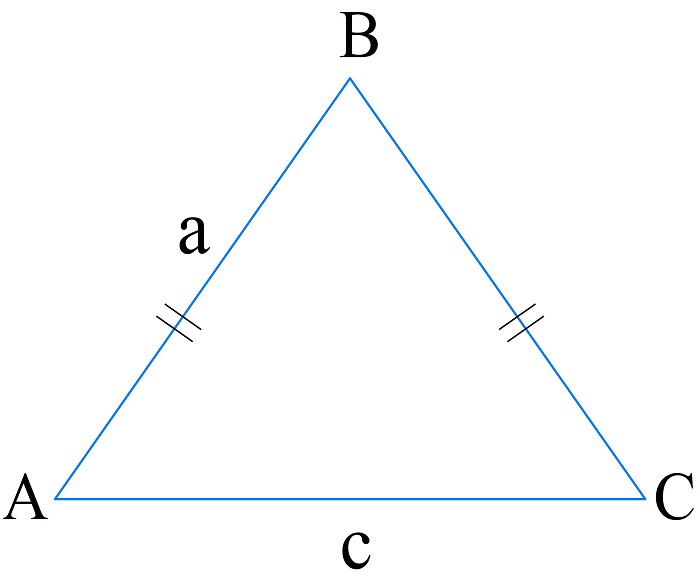
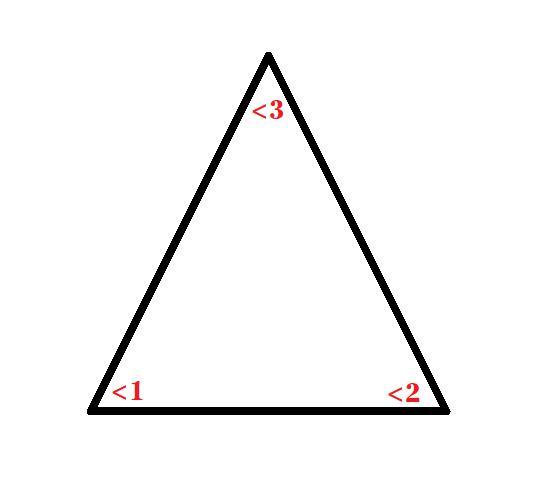

Чтобы правильно решать задачи с таким треугольником, всегда помните, что два угла по 70° — это углы при основании, а угол при вершине равен 40°.
Схема электропроводки в квартире. Архитектура электропроводки.

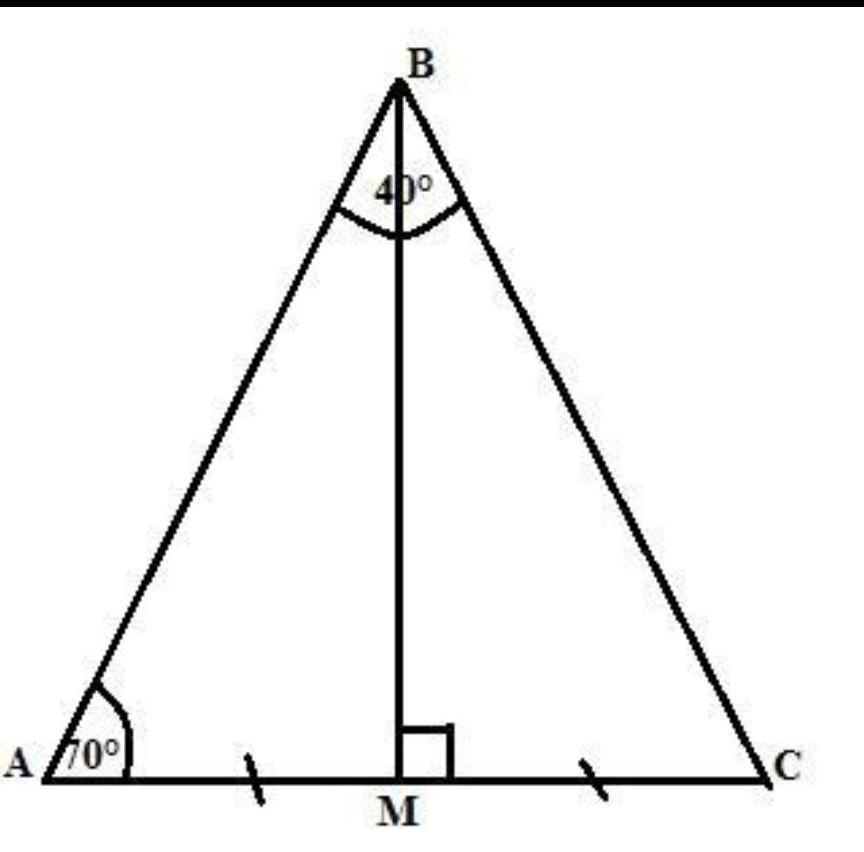
Если вам нужно найти высоту такого треугольника, используйте формулы для вычисления высоты равнобедренного треугольника через его основание и углы.

Треугольник с углами 40°, 70°, 70° – равнобедренный. - ОГЭ 2017 - ЗАДАНИЕ 13 - ШКОЛА ПИФАГОРА


При расчетах сторон треугольника применяйте теорему синусов, которая поможет найти все неизвестные стороны, если известен хотя бы один угол и его противоположная сторона.

Измерение угла с помощью транспортира
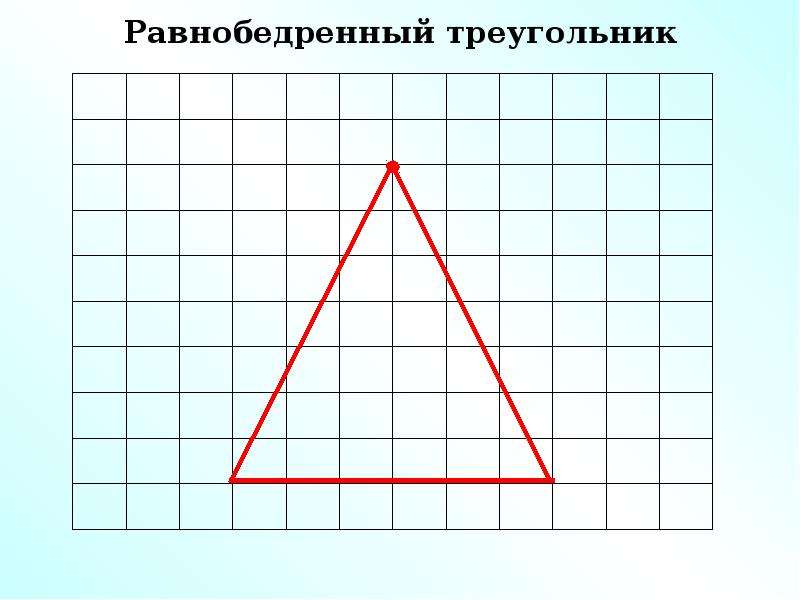
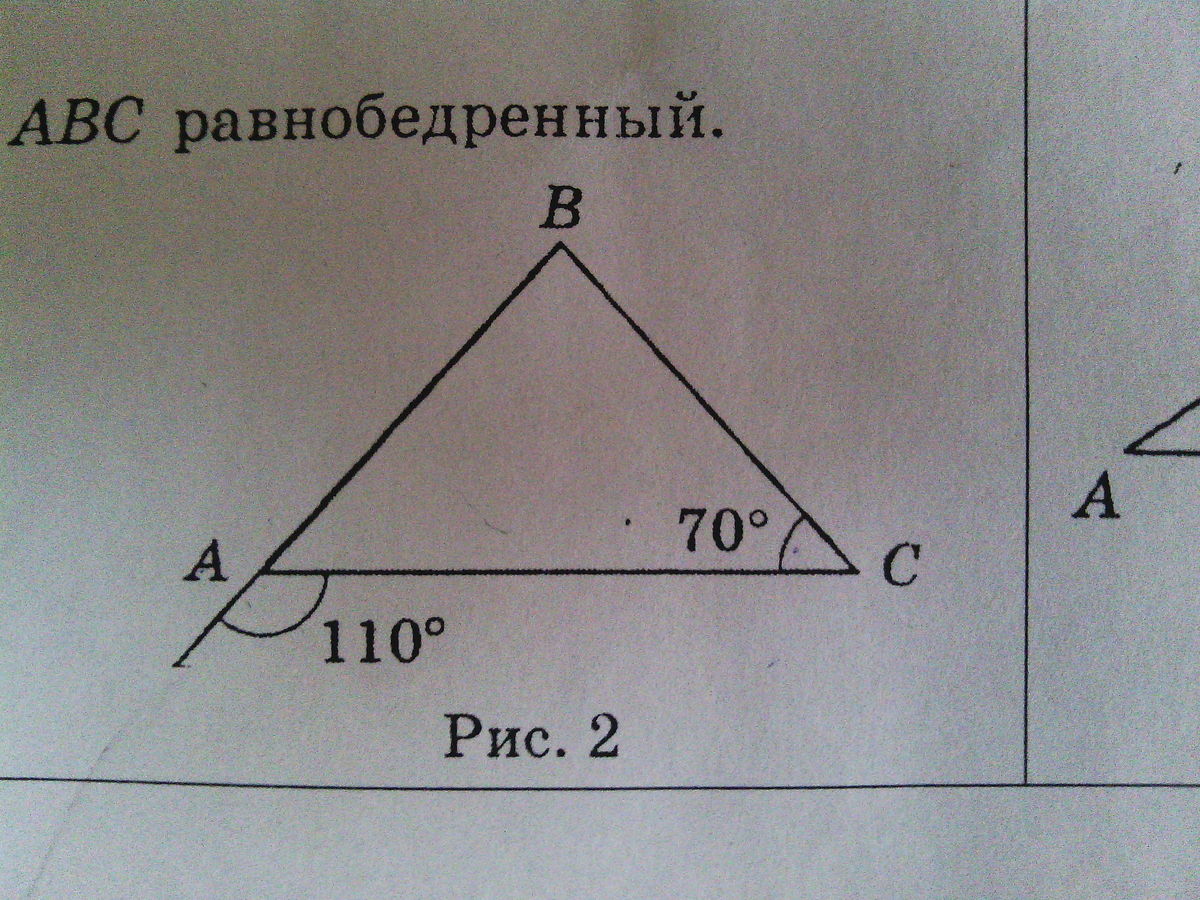
Для удобства рисования треугольников с углами 40° и 70° используйте транспортир для точной отметки углов на бумаге.

Равнобедренный треугольник. Свойства равнобедренного треугольника - Математика - TutorOnline
Если вы работаете с такими треугольниками в контексте черчения, убедитесь, что правильно определили точку пересечения высоты с основанием, так как это важно для симметрии.
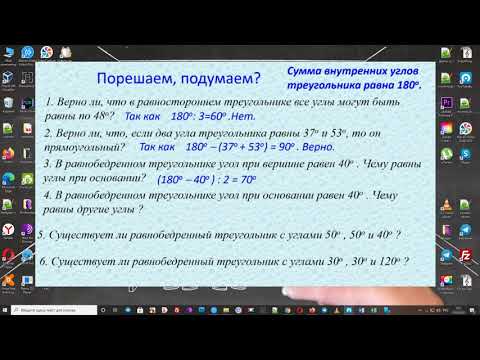
Треугольник с углами равнобедренный верно или нету
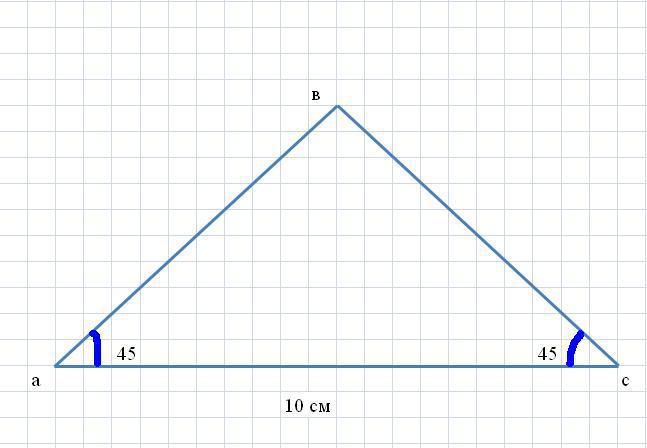
Для вычисления площади треугольника с углами 40° и 70° можно использовать формулу для площади через основание и высоту: S = (1/2) * основание * высота.
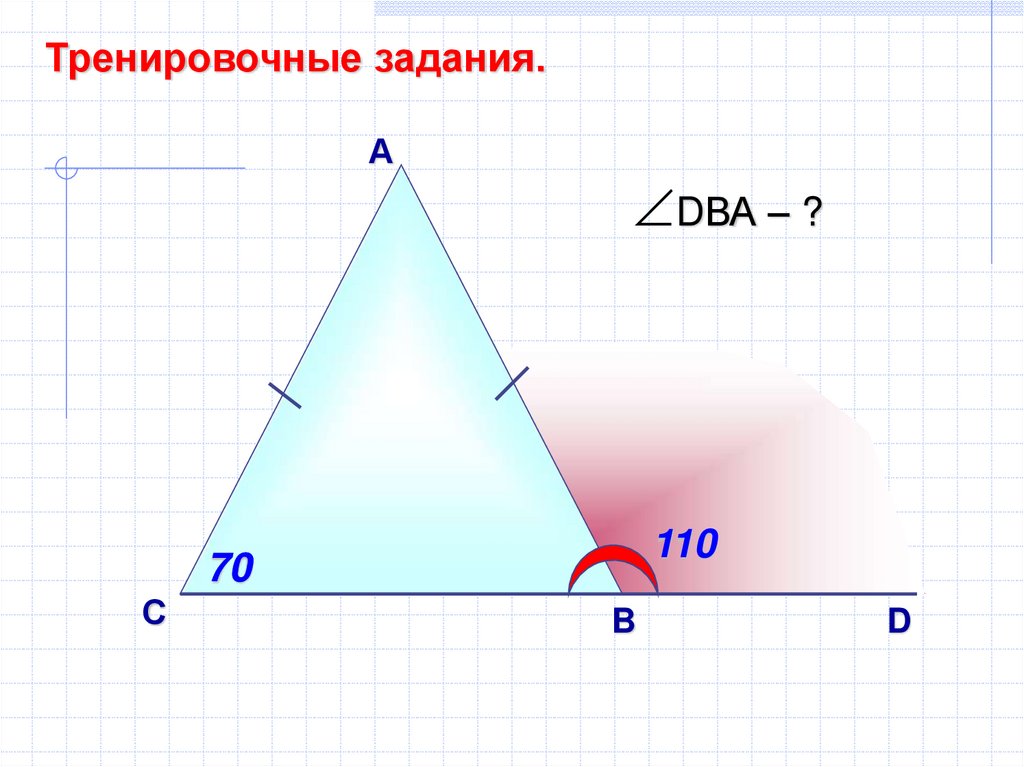
Учтите, что равнобедренный треугольник с углами 40° и 70° имеет ось симметрии, которая делит его на два одинаковых равных прямоугольных треугольника.
Признаки равенства треугольников. Практическая часть. 7 класс.
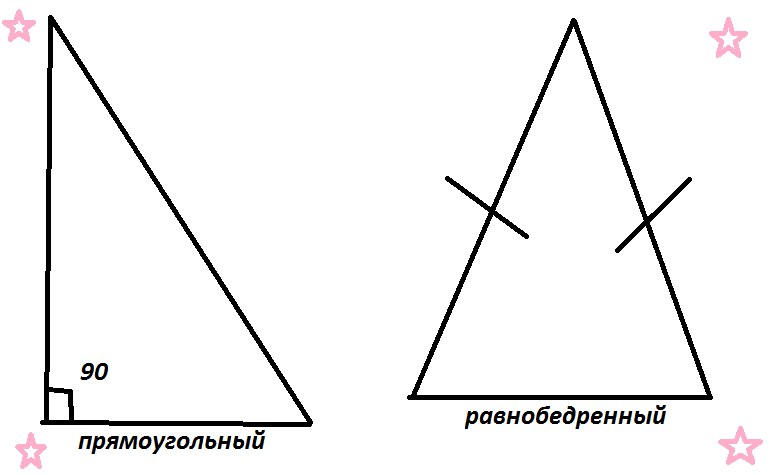
Если треугольник используется в строительных расчетах, важно учитывать его свойства для правильного распределения нагрузок, особенно в конструкции крыш или каркасных элементов.
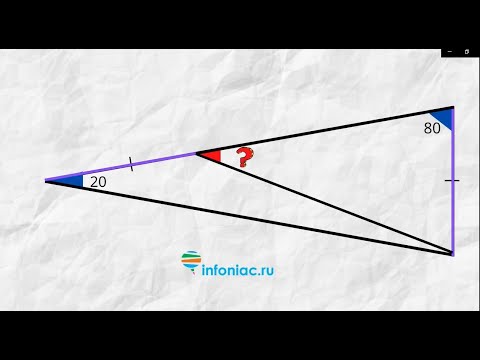
Непростая задача с интересным решением: Найдите угол в треугольнике
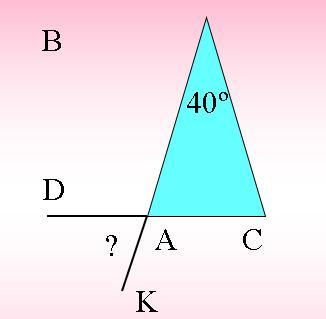
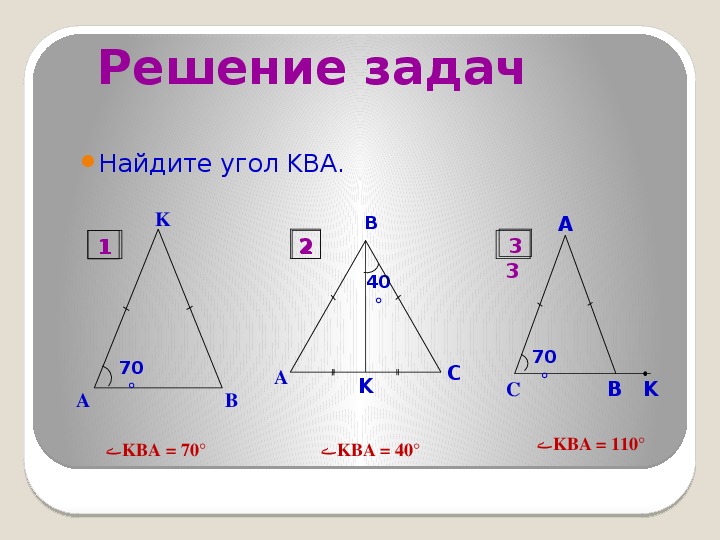
При решении задач с такими треугольниками, где нужно найти периметр, достаточно сложить все стороны, используя подходящие геометрические методы.
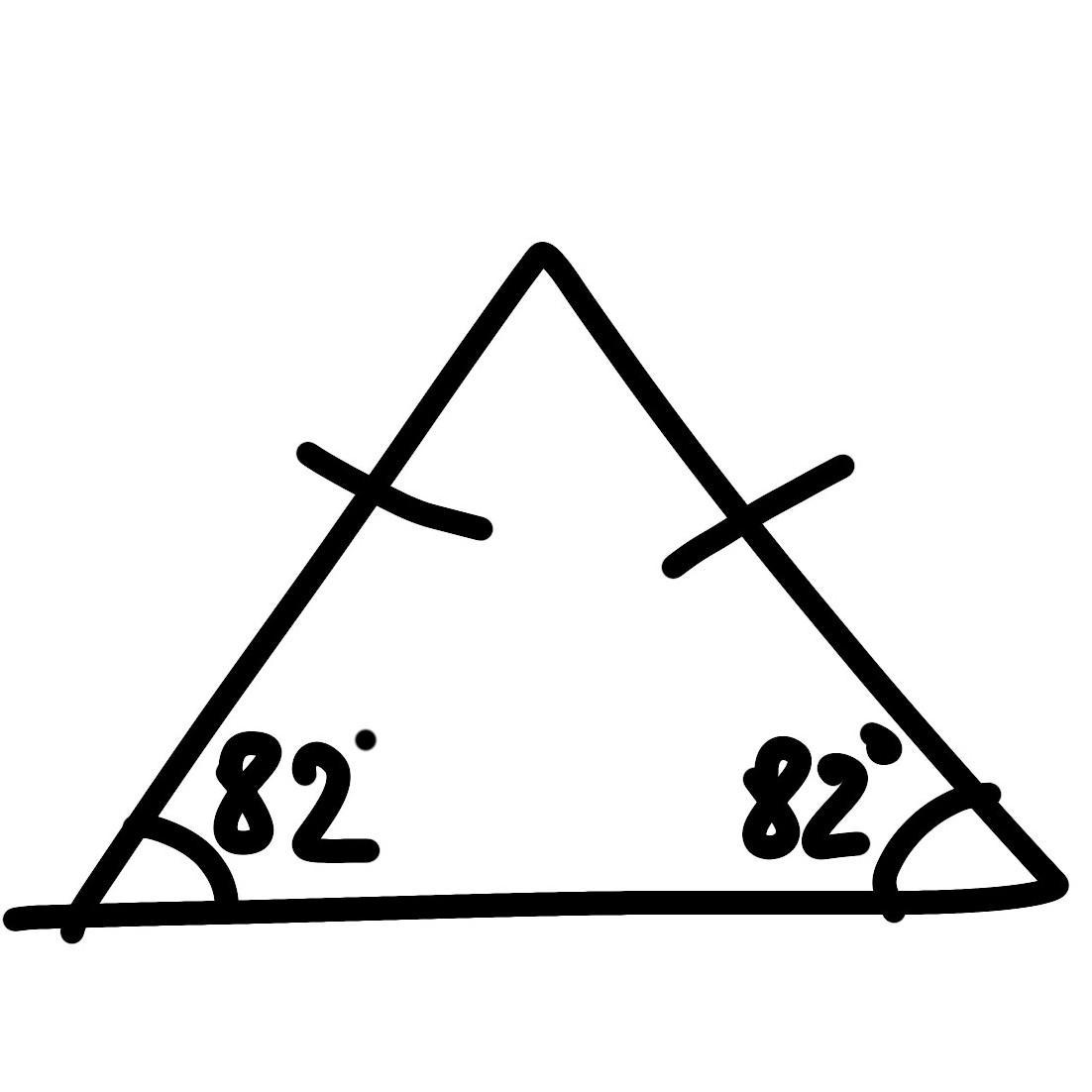
Для более точного построения треугольников с углами 40° и 70° можно использовать программное обеспечение для черчения, которое обеспечит нужную точность углов и размеров.


ВНЕШНИЕ УГЛЫ ТРЕУГОЛЬНИКА 😉 #shorts #математика #егэ #огэ #профильныйегэ