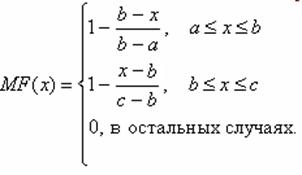Понимание и применение треугольной функции принадлежности в разных областях знаний
Треугольная функция принадлежности — это один из основных методов в теории нечетких множеств, используемый для описания неопределенности в данных и принятия решений в условиях неопределенности. В данной статье мы рассмотрим основные принципы ее работы, а также советы по применению этого инструмента в различных сферах.
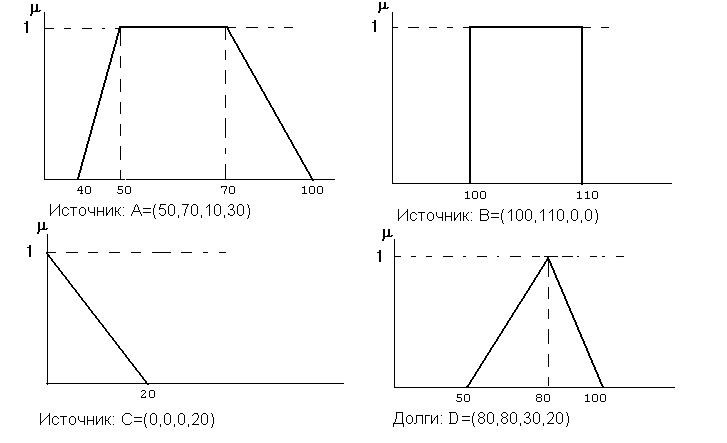

Треугольная функция принадлежности хорошо подходит для ситуаций, где данные имеют четкую структуру, но могут быть подвержены неопределенности. Это полезно для моделирования явлений, которые невозможно точно измерить.

Раскрываю 8 новых решений для ванной, которые будут в тренде в 2024 году
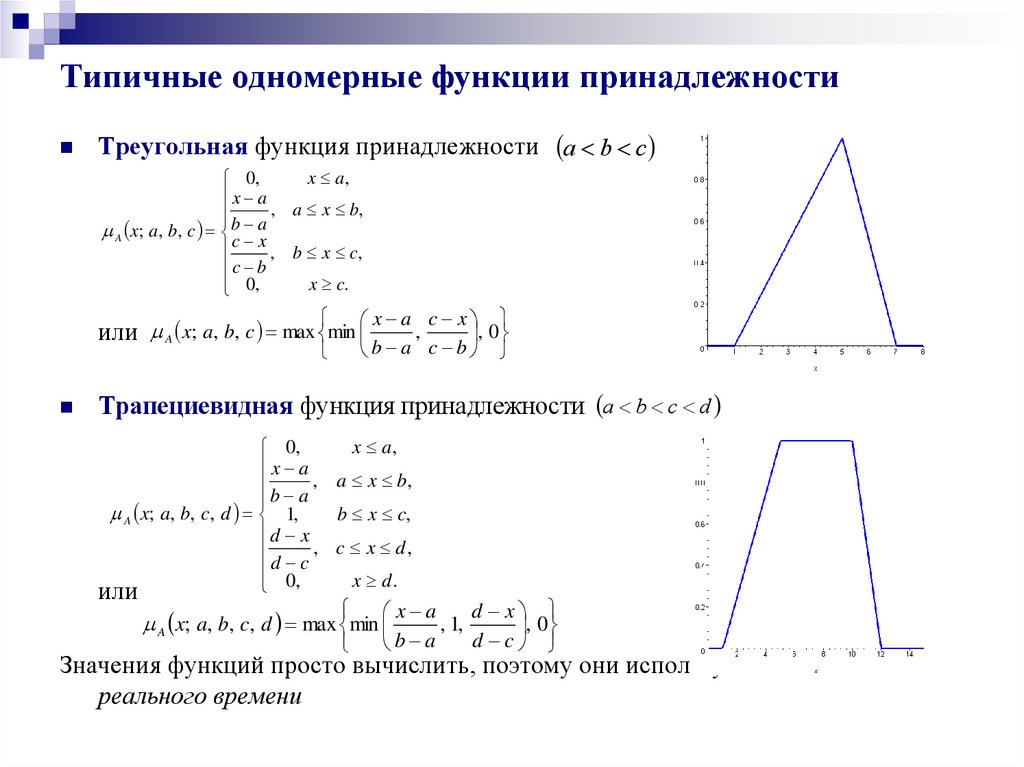
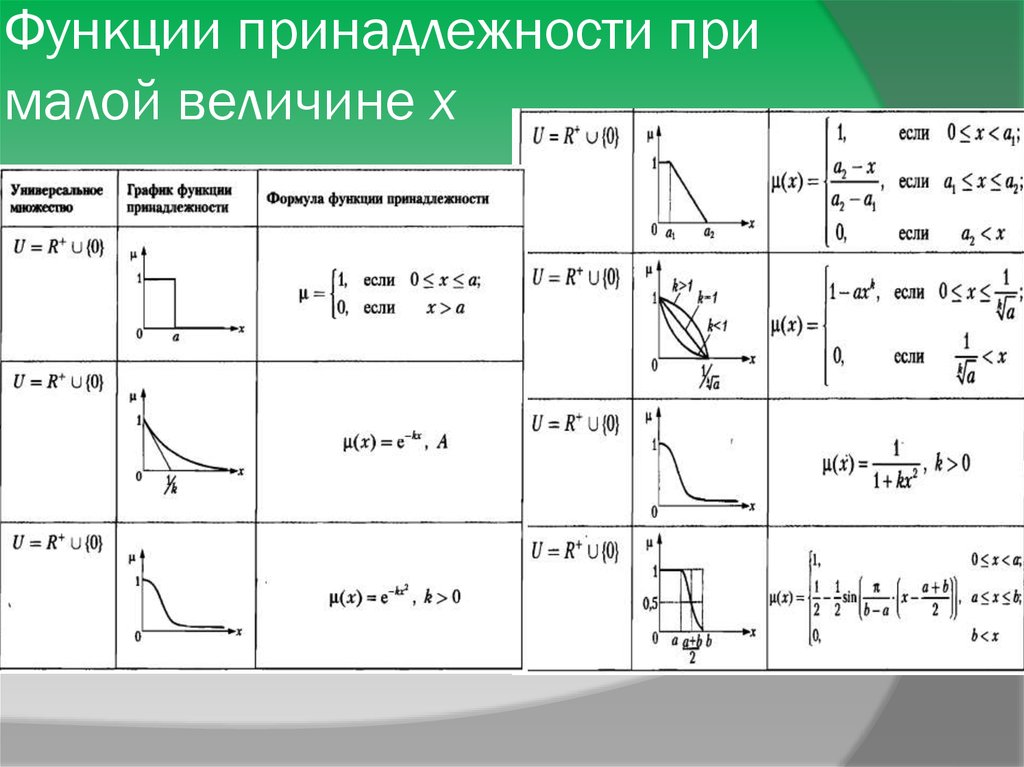
Используйте треугольную функцию для упрощения расчетов в системах, где необходимо учитывать диапазоны значений, а не точные данные. Это значительно повысит гибкость модели.

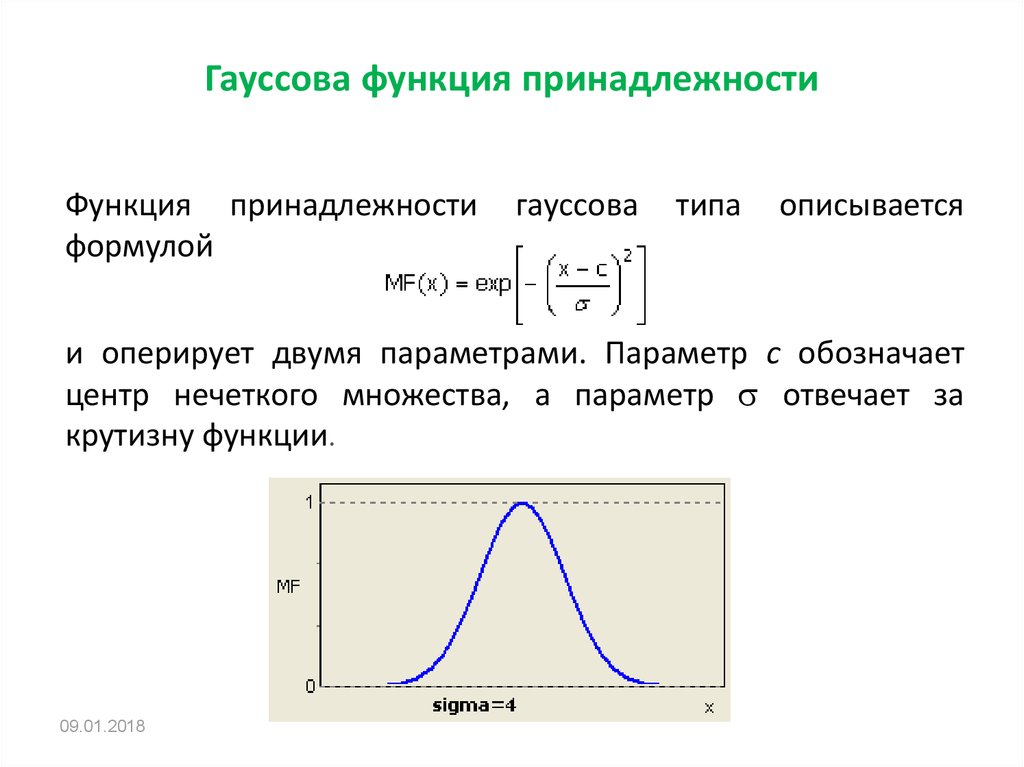
Обзор функций принадлежностей нечётких множеств
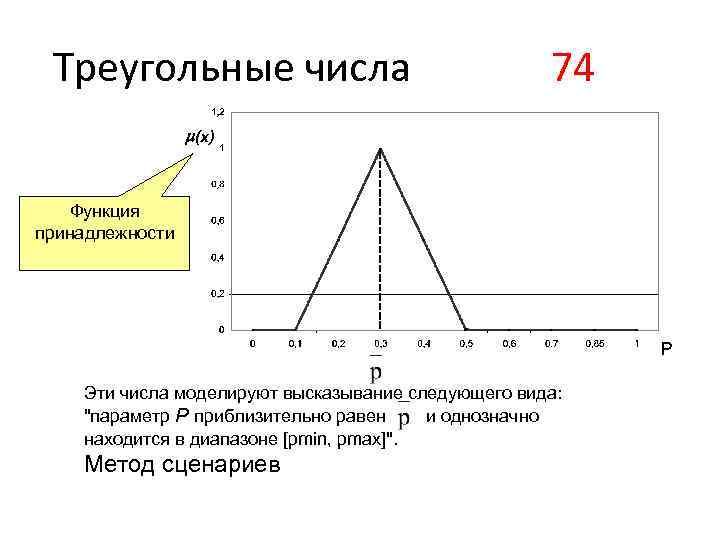
Понимание того, как настраиваются параметры треугольной функции принадлежности, поможет вам адаптировать модель под конкретные задачи и снизить погрешности в расчетах.

Точки разрыва функции // Высшая Математика
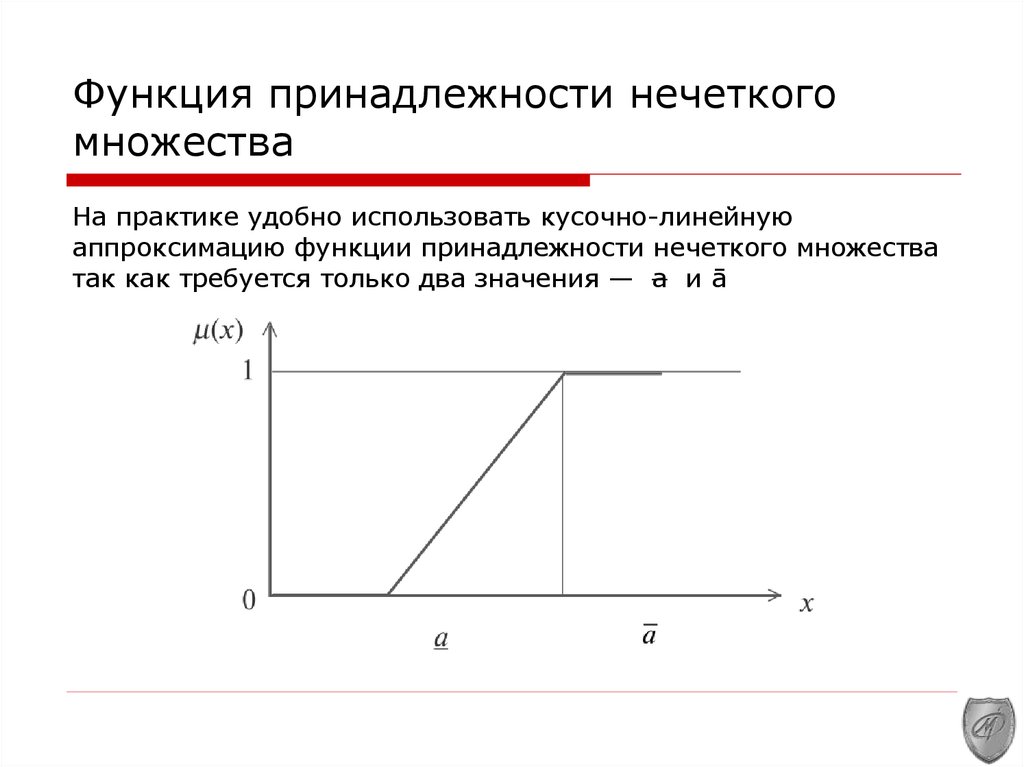
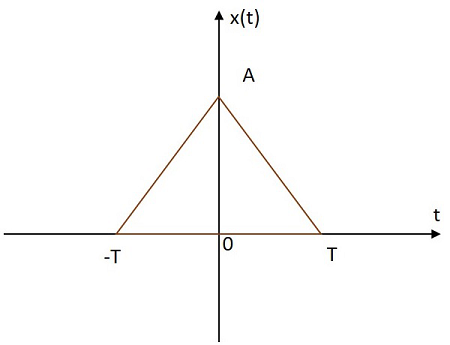
Для улучшения точности моделей, основанных на треугольных функциях, важно правильно выбирать границы и пик треугольника, так как от этого зависит качество результата.

Парадокс Бертрана – что не так со случайностью // Vital Math
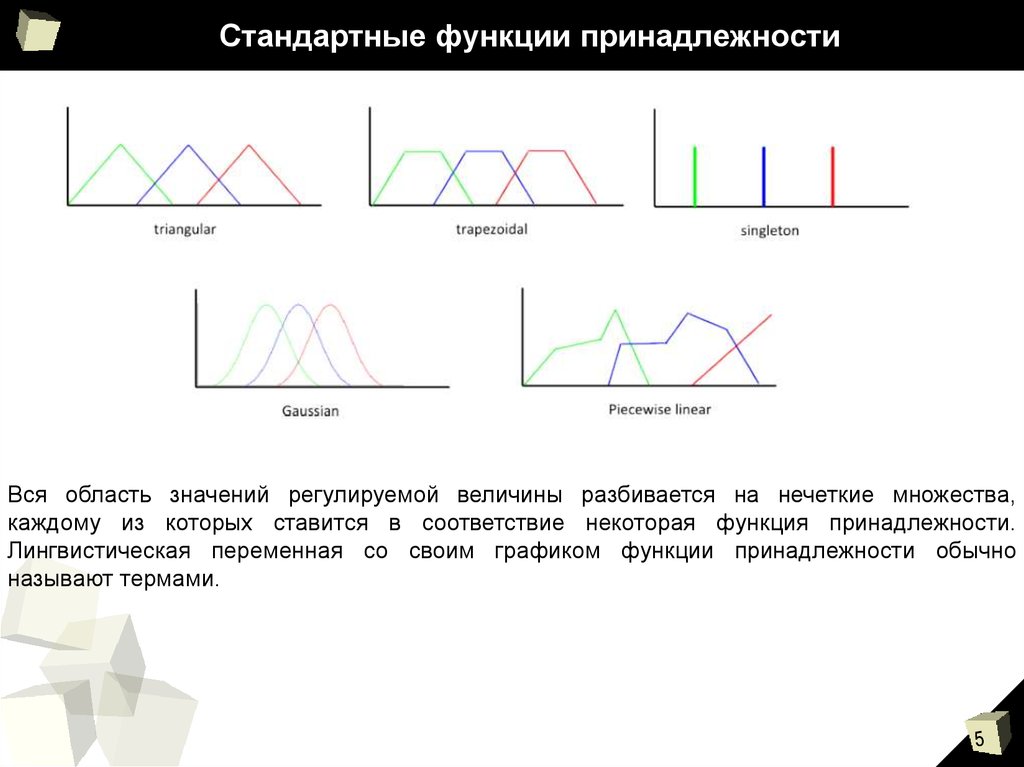
Если необходимо учитывать несколько источников неопределенности, рассмотрите возможность комбинирования треугольных функций с другими методами нечеткой логики для получения более надежных решений.

Метод Розебома
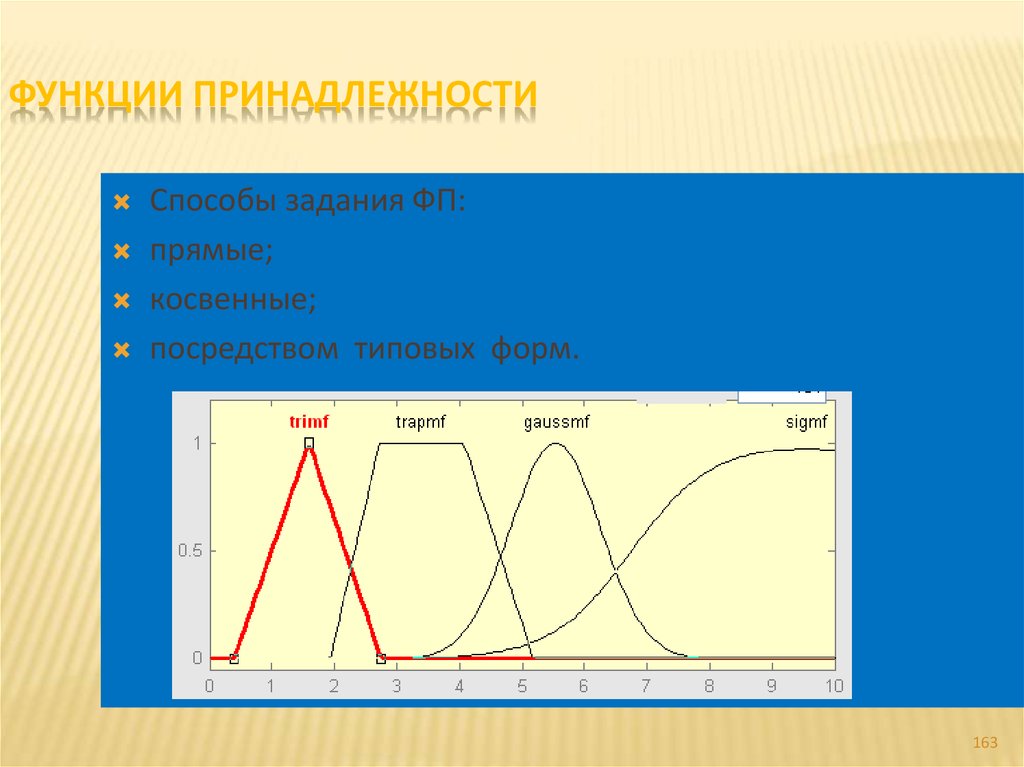
При применении треугольных функций для принятия решений важно также учитывать контекст задачи: чем точнее вы определяете границы, тем точнее будет ваше решение.
Функции принадлежности нечётких множеств в Mathcad
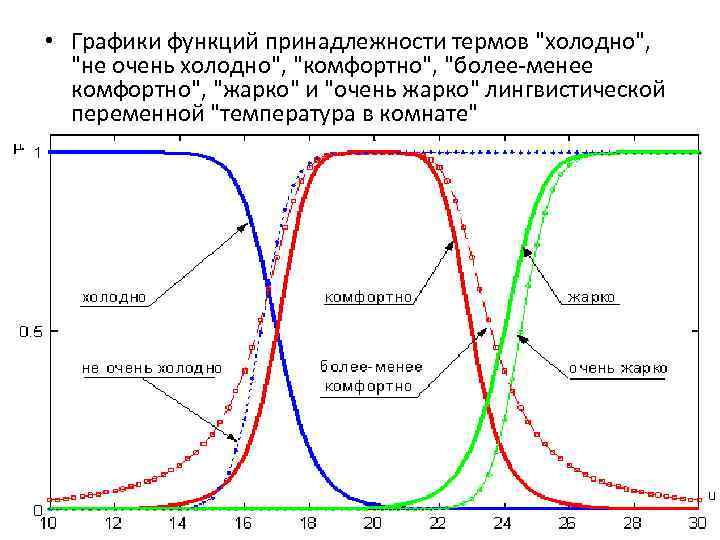

Моделирование с помощью треугольных функций является эффективным инструментом при анализе и прогнозировании процессов, связанных с неопределенностью, например, в экономике или инженерии.
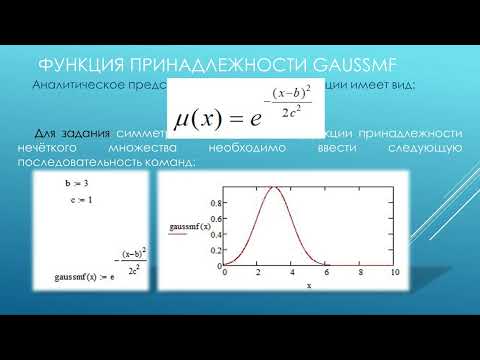
Построение в Mathcad функций принадлежности нечётких множеств
Применение треугольной функции принадлежности в искусственном интеллекте помогает улучшить адаптивность систем, позволяя более точно реагировать на изменения в данных и условиях.

TRIANGULAR LOAD Shear and Moment Diagrams EXAMPLE PROBLEM

Wolframalpha: аналитическое задание функций принадлежности нечётких множеств
В сочетании с другими методами нечеткой логики треугольная функция может быть использована для создания более сложных моделей, которые способны учитывать множество факторов влияния.
НЛ Типовые функции принадлежности и БИП

Не забывайте, что при расширении модели и усложнении ее компонентов, необходимо периодически пересматривать настройки треугольной функции принадлежности для сохранения точности решений.