Основные методы вычисления трехкратных интегралов для решения практических задач
Трехкратный интеграл — это важный инструмент в математике и физике, используемый для вычисления объемов и масс в трехмерных пространствах. В этой статье мы разберем основные принципы его вычисления, а также предложим полезные советы для эффективного решения задач с использованием трехкратных интегралов.



Для начала всегда проверяйте область интегрирования и убедитесь, что вы правильно определили пределы интеграции для каждой переменной.

Математический анализ, 44 урок, Тройной интеграл

Используйте подходящие координатные системы (например, цилиндрические или сферические), чтобы упростить вычисления трехкратного интеграла.

Практика 5. Тройной интеграл

Не забывайте про изменение порядка интегрирования, если это позволяет упростить выражения или облегчить расчет.
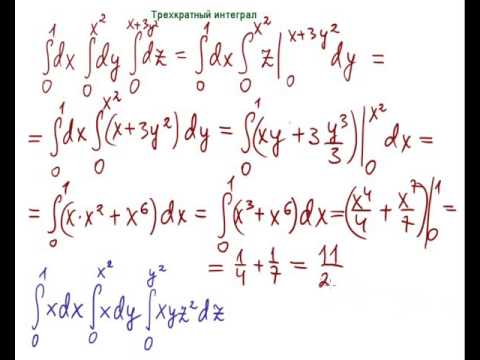
Трехкратный интеграл

Для вычисления массы тела используйте плотность в пределах заданной области, помня, что плотность может зависеть от координат.

Семинар 6. Тройной интеграл.
Если задача требует вычисления объема, то учтите, что трехкратный интеграл позволяет учитывать любые формы и границы объектов в трехмерном пространстве.

ТРОЙНОЙ ИНТЕГРАЛ. СФЕРИЧЕСКИЕ КООРДИНАТЫ


Для сложных задач делите их на более простые части, вычисляя трехкратные интегралы поэтапно для разных областей.
Обязательно применяйте теоремы о смене переменных, когда область интегрирования имеет симметричную форму, например, в случае цилиндрических или сферических координат.
Постоянно сверяйтесь с физическим смыслом задачи — важно понимать, что означает каждая переменная и как она влияет на итоговый результат.

МИШЕНЬКА УЧАСТВОВАЛ В ПОЛУФИНАЛЕ ICPC! РАЗБОР КРАСИВЫХ ЗАДАЧ ОТ ГРОССМЕЙСТЕРА ПРОГРАММИРОВАНИЯ!

Используйте графическое представление области интегрирования, чтобы легче понять, как проходит интеграция и где находятся границы области.


Не забывайте, что для точных результатов необходимо правильно учитывать все параметры и условия задачи, чтобы избежать ошибок при вычислениях.
