Исследование телесного угла конуса: основы и практическое применение
На данной странице собраны полезные советы и рекомендации по теме телесного угла конуса, что является важным аспектом в геометрии и инженерии. Мы рассмотрим, как точно определить этот угол, его использование в различных задачах и научим, как правильно работать с такими геометрическими фигурами.


Телесный угол конуса можно вычислить через угол между образующими и осью фигуры. Это важный шаг для правильного понимания структуры конуса.

Конус Морзе №2 От и до.

При изучении телесных углов конуса важно учитывать соотношение высоты и радиуса основания, чтобы точно определить параметры угла.

как быстро проточить конус не используя малые продольные салазки
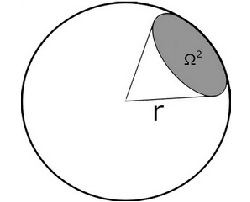
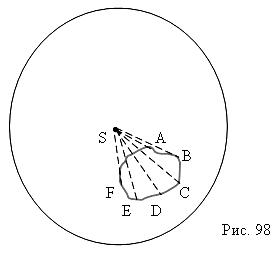
Чтобы вычислить телесный угол, используйте формулу, которая включает в себя длину образующей и радиус основания конуса.

Лекция 3 - Стохастическая геометрия - Дмитрий Запорожец - Лекториум
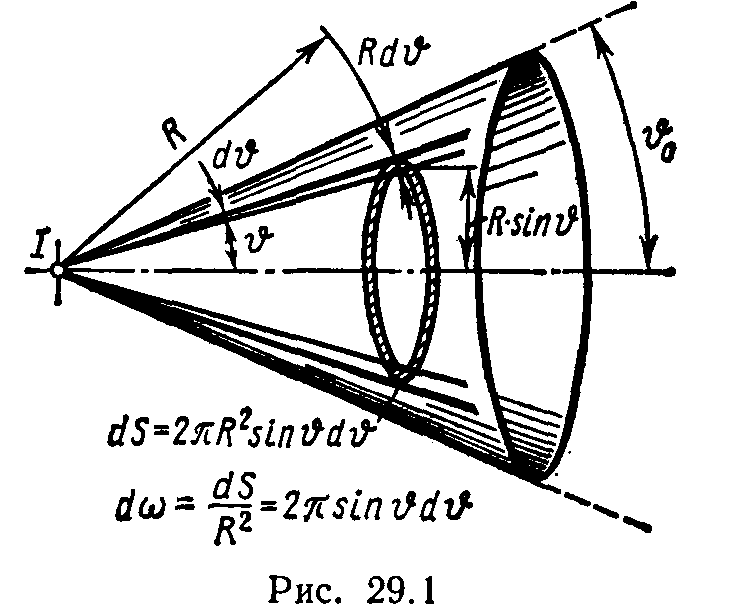
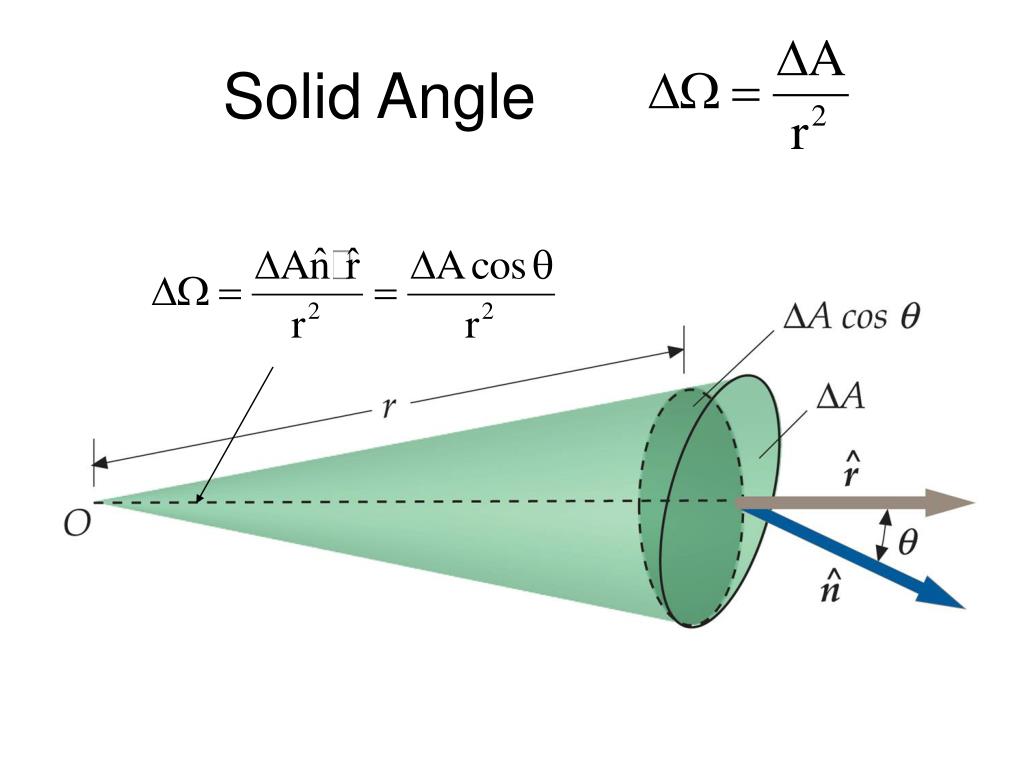
Если вы работаете с несколькими конусами, всегда учитывайте их ориентацию в пространстве для точных расчетов углов.

Лекция 7 - Стохастическая геометрия - Дмитрий Запорожец, Татьяна Мосеева - Лекториум

Для практических задач, связанных с конусом, важно точно измерять высоту и радиус основания, чтобы избежать ошибок при определении углов.

Электромагнетизм Пр3.5. Телесный угол конуса. Нахождение радиального поля над диском
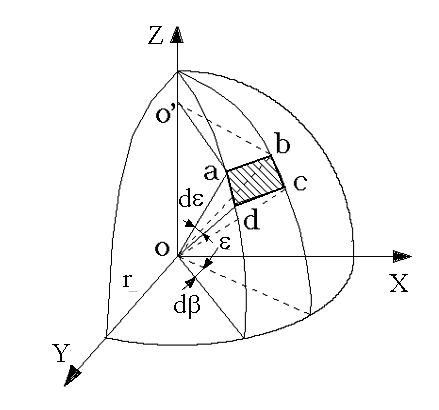
Когда работаешь с конусами, всегда проверяй правильность построений на чертежах, чтобы убедиться, что углы соответствуют расчетам.
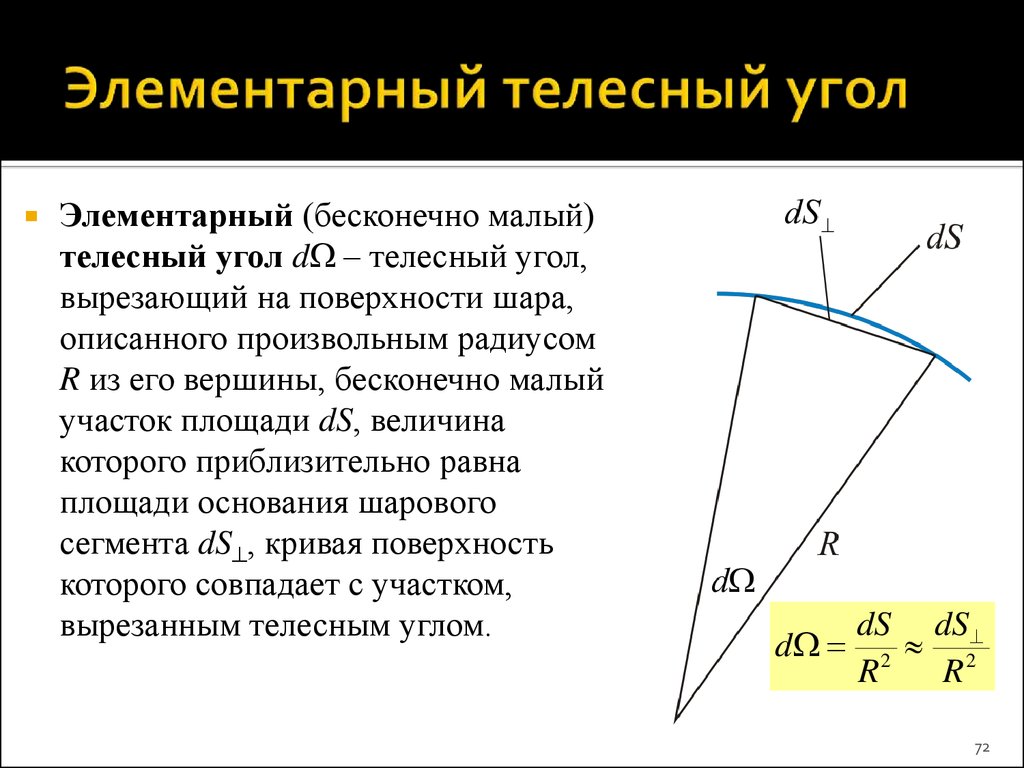
В случае с усеченными конусами, важно учитывать два телесных угла — для верхней и нижней части фигуры.
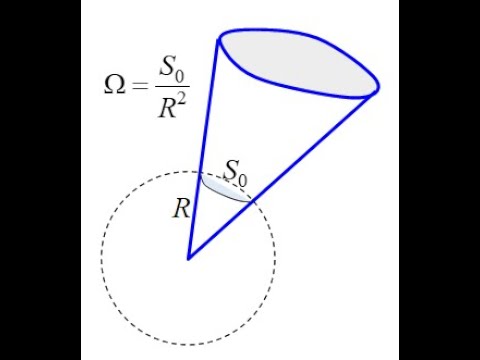
Теорема Гаусса - доказательство.
Для расчета угла между двумя конусами в пространстве, используйте методы векторной геометрии, чтобы повысить точность расчетов.
20.04.2020 МАТЕМАТИКА, Федякова, 1 курс КОНУС

Физика 10 класс. Занятие 19. Теорема Гаусса. Примеры
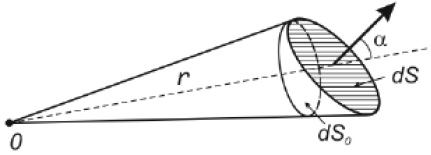
При решении задач с конусами всегда проверяйте единицы измерений — они должны быть согласованы во всех расчетах.

ГЕОМЕТРИЯ 11 класс: Конус Площадь конуса. Усеченный конус
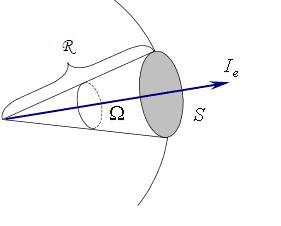
Не забывайте о возможных погрешностях при использовании телесных углов в реальных инженерных задачах, особенно при моделировании сложных объектов.
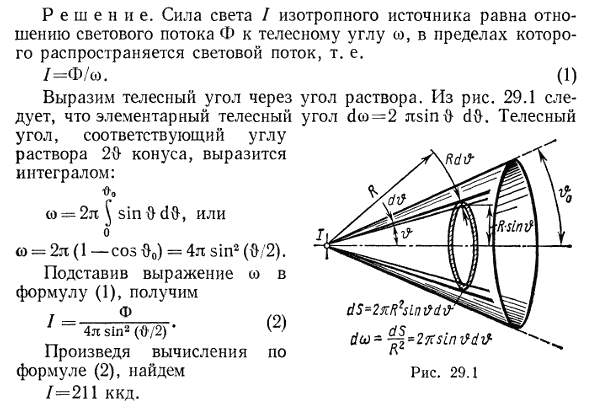

Сделать конус на токарном? Элементарно!