Основное свойство соответственных углов: их сумма всегда составляет 180 градусов
Сумма соответственных углов, возникающих при пересечении двух прямых, всегда равна 180 градусам. Это важное правило геометрии, которое используется для решения множества задач в разных областях математики. Понимание этой концепции помогает в работе с параллельными прямыми, многоугольниками и других геометрических фигурах.

При решении задач на геометрию всегда обращайте внимание на положения прямых: если они пересекаются под углом, значит, могут быть использованы свойства соответственных углов.

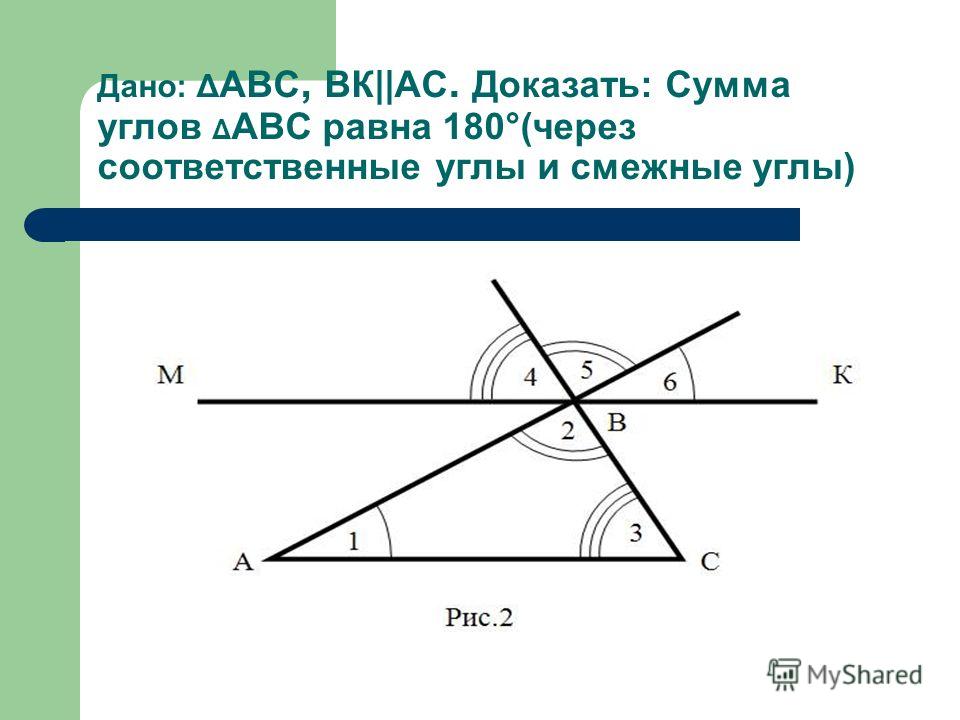
ПОЧЕМУ СУММА УГЛОВ В ТРЕУГОЛЬНИКЕ РАВНА 180? #shorts #геометрия #егэ #огэ #треугольник
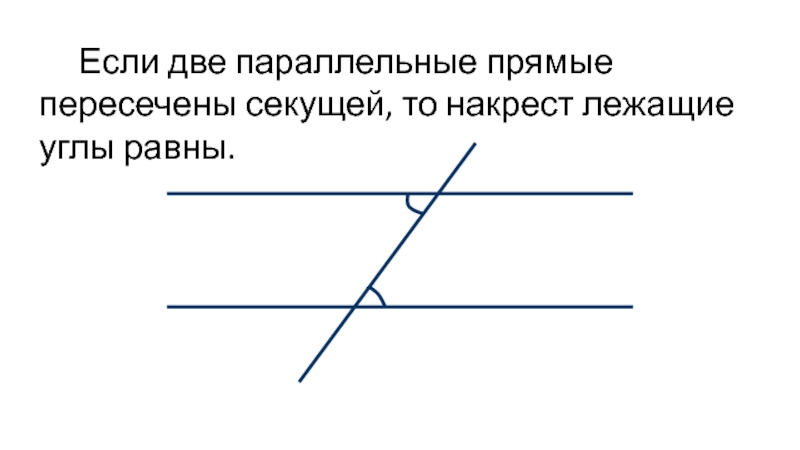
Для наглядности всегда рисуйте схему задачи, это поможет лучше понять расположение углов и легче заметить, что сумма соответственных углов равна 180 градусам.

7 класс. Глава4 - Параллельные прямые. Сумма односторонних углов 180 градусов

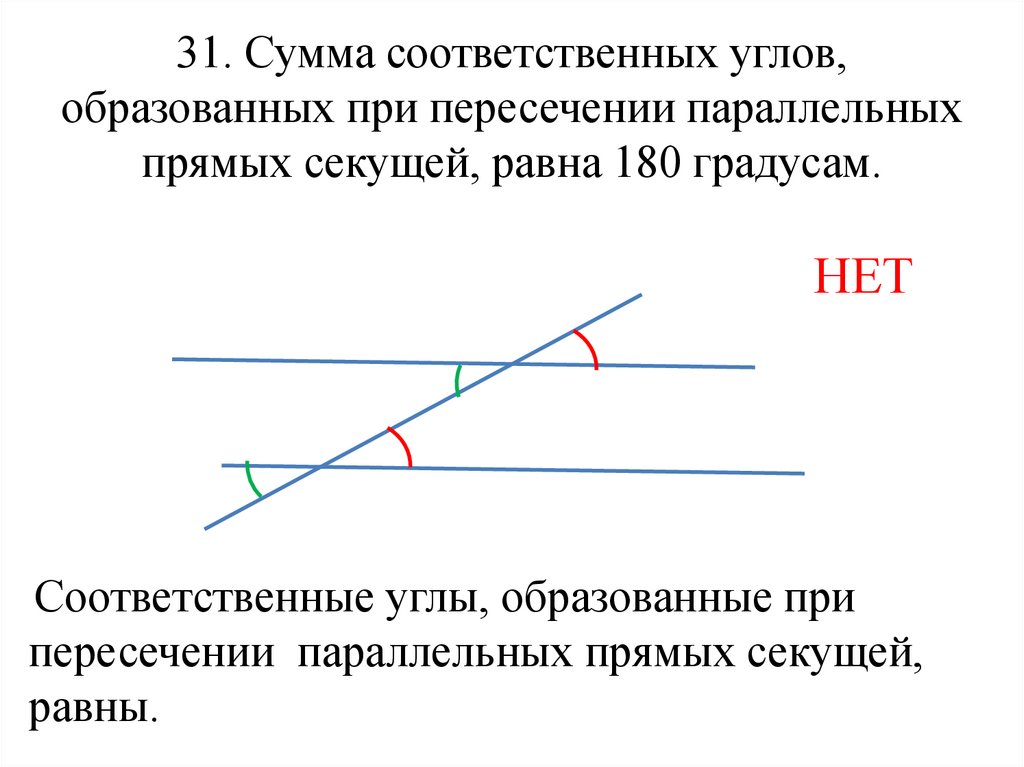
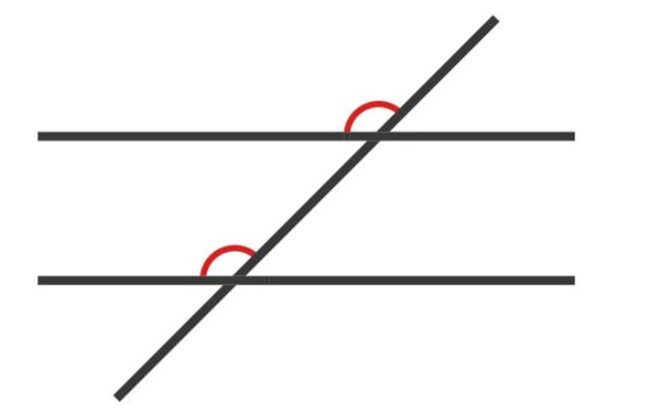
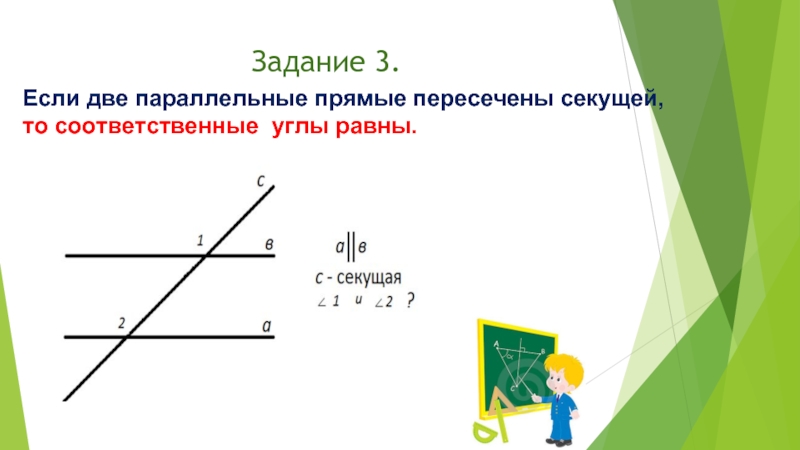
При работе с параллельными прямыми и секущими помните, что соответственные углы равны между собой, что дает возможность вычислять остальные углы.

7 класс, 11 урок, Смежные и вертикальные углы
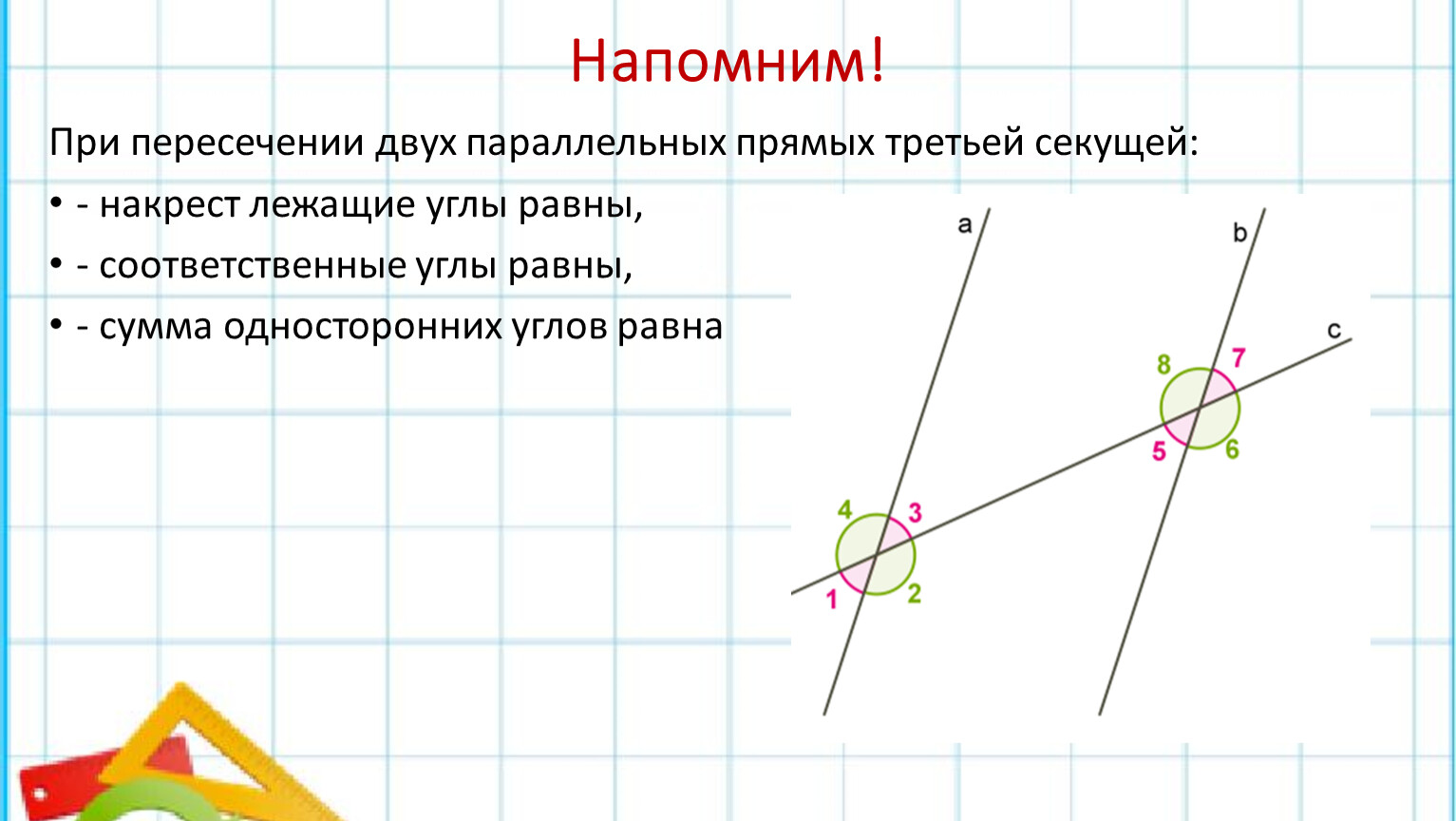
Используйте свойства соответственных углов для упрощения сложных задач: достаточно вычислить один угол, чтобы найти остальные.

7 класс. Глава4 - Параллельные прямые. сумма односторонних углов равна 180 градусов

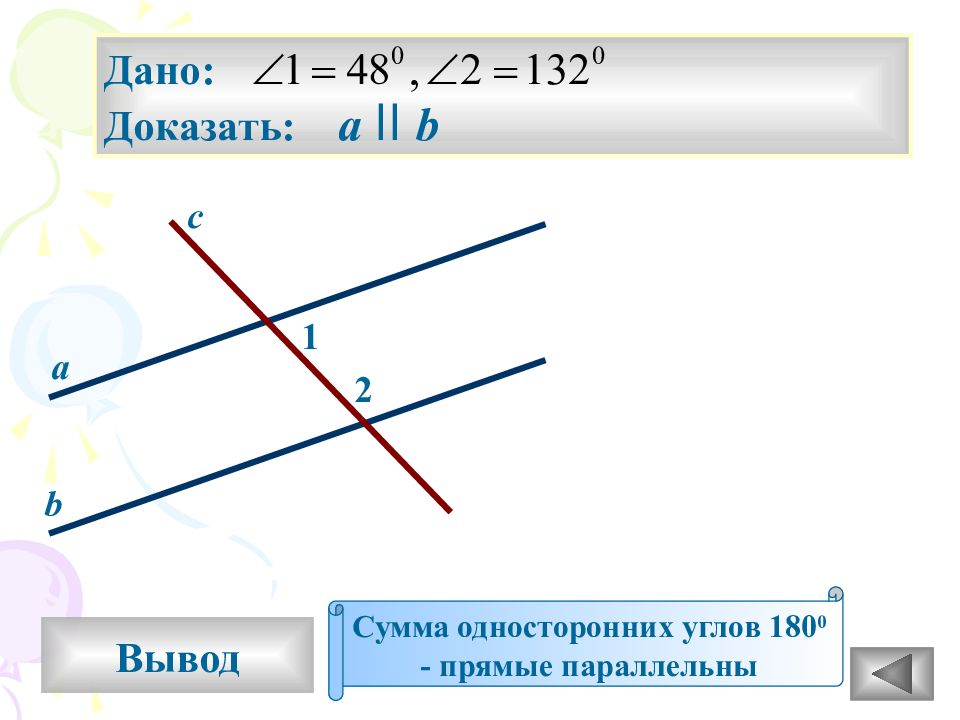
Если вам нужно доказать, что прямые параллельны, то можно использовать факт, что сумма соответственных углов равна 180 градусам.
Равенство соответственных углов


Не забывайте, что это правило работает только для прямых, пересекаемых одной секущей, и в случае, если углы соответственные.

При работе с многоугольниками можно применять свойства соответственных углов, чтобы найти неизвестные углы и упростить решение задачи.

Использование теоремы о сумме соответственных углов помогает при решении задач на геометрические доказательства и анализ конструкции.

Доказательство 2 и 3 признаков параллельности прямых.
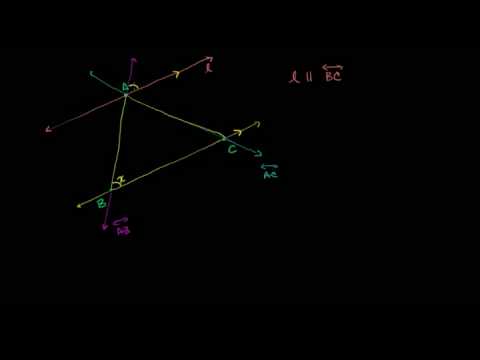
Сумма углов треугольника равна 180

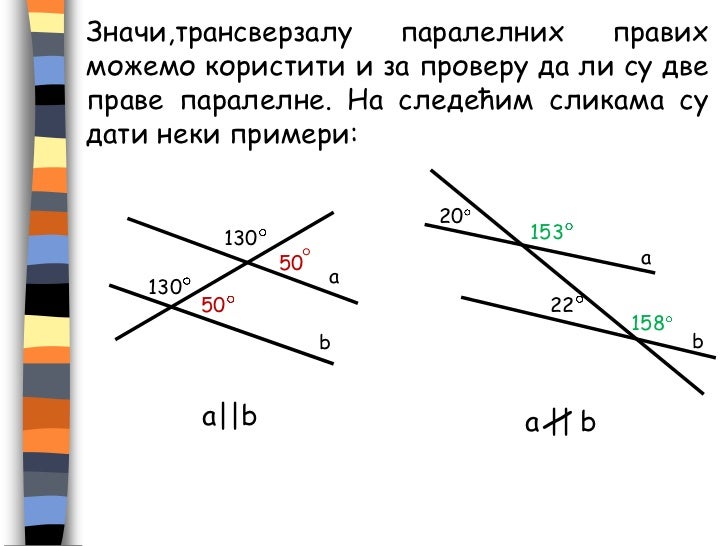
Помните, что иногда для использования этого правила требуется дополнительное обоснование, например, доказательство параллельности прямых.


Чтобы избежать ошибок, всегда проверяйте, что углы действительно соответственные, и находятся ли прямые, образующие эти углы, в нужном положении.

ОГЭ. 9 класс. Модуль Геометрия. Укажите номера верных утверждений