Как находить стационарные точки и анализировать экстремумы функций
На этой странице представлены полезные советы и визуальные примеры для анализа стационарных и критических точек, а также для нахождения экстремумов функций. Эти концепции являются основой для решения множества задач в математике, особенно в анализе функций и оптимизации. Понимание того, как правильно работать с такими точками, поможет вам уверенно решать задачи и улучшать математические навыки.

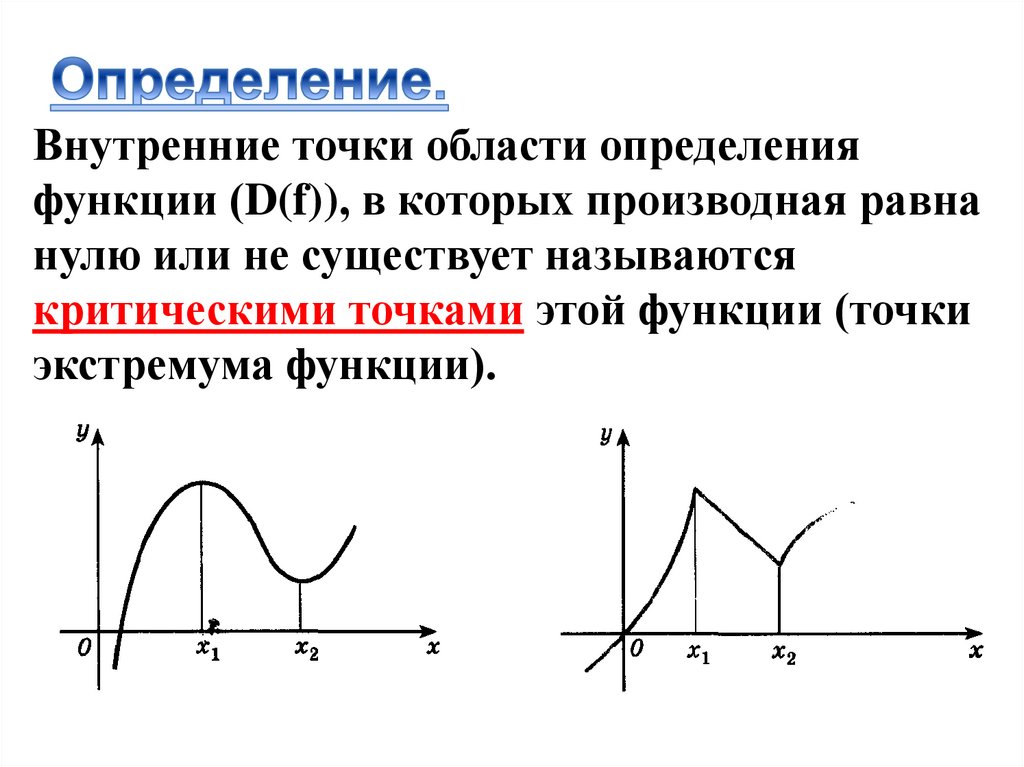

Для нахождения стационарных точек необходимо приравнять производную функции к нулю и решить полученное уравнение.

Найти точки экстремума функции


Важно помнить, что не все стационарные точки являются точками экстремума — для этого нужно анализировать знак второй производной или использовать другие методы.

АЛГЕБРА С НУЛЯ — Точки Экстремума Функции
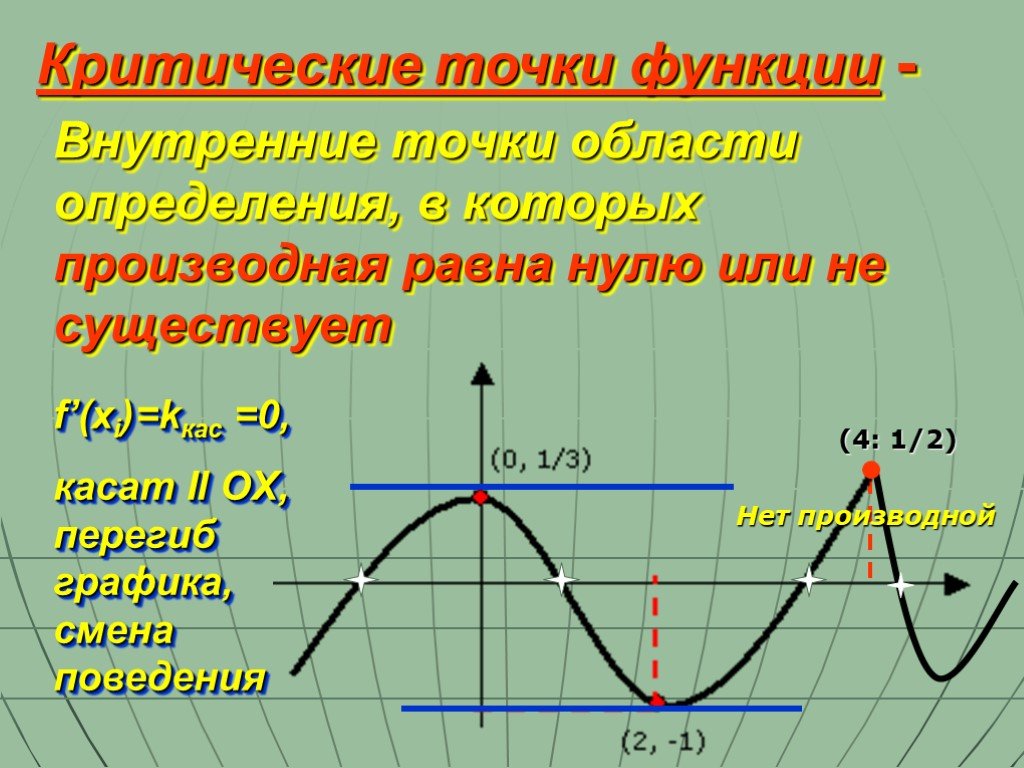
Для анализа критической точки нужно вычислить производную функции и проверить, равна ли она нулю или не существует в данной точке.

Урок 12. Экстремумы функции. Алгебра 11 класс
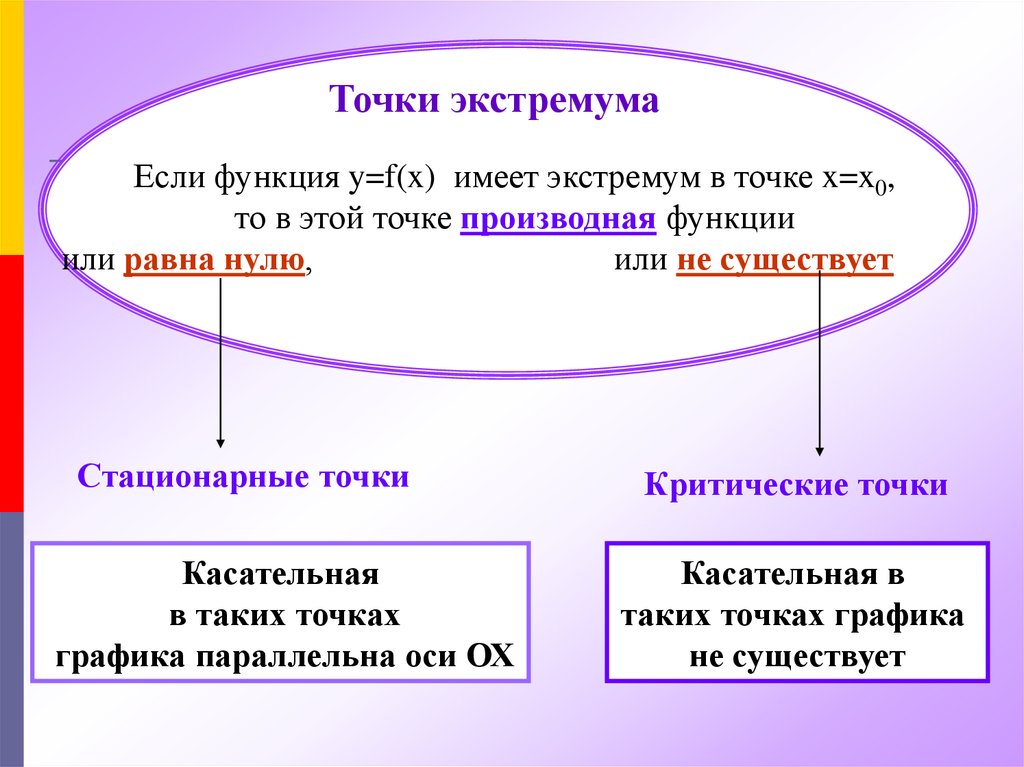
Если в точке функция меняет направление (например, из возрастания в убывание или наоборот), это может свидетельствовать о наличии экстремума.
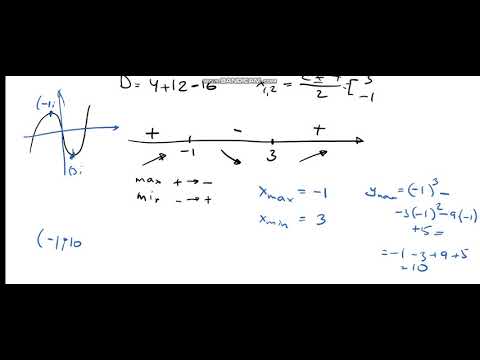
Критические точки функции
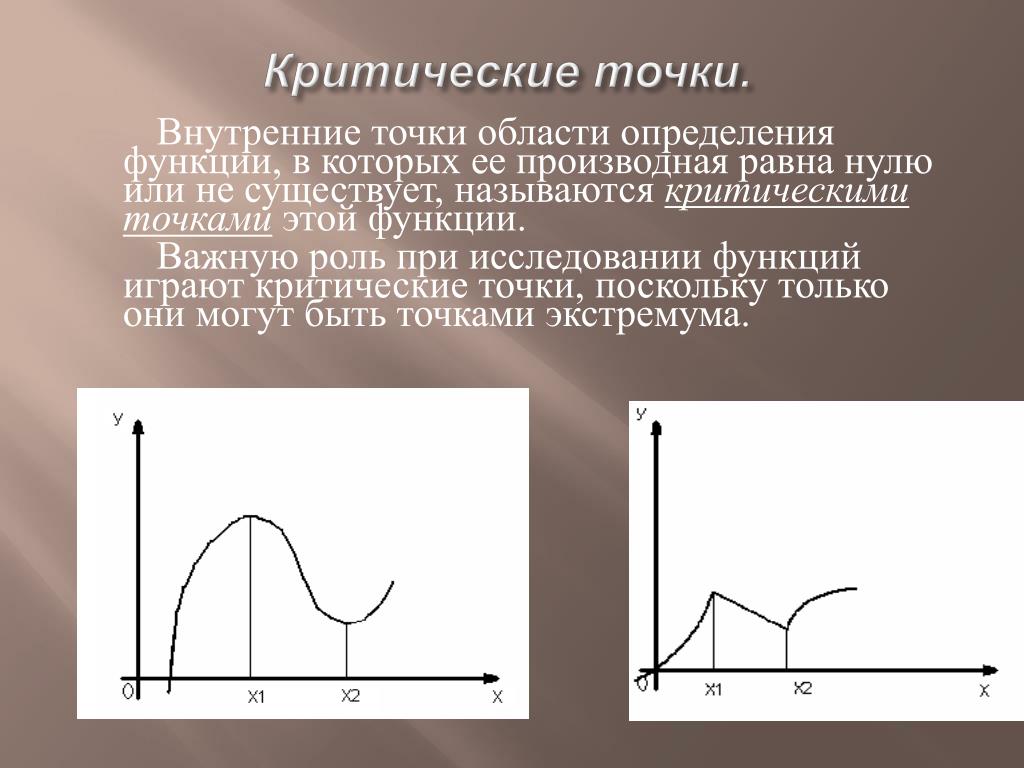
Для нахождения глобального экстремума важно учитывать не только производную, но и поведение функции на концах промежутка или области определения.
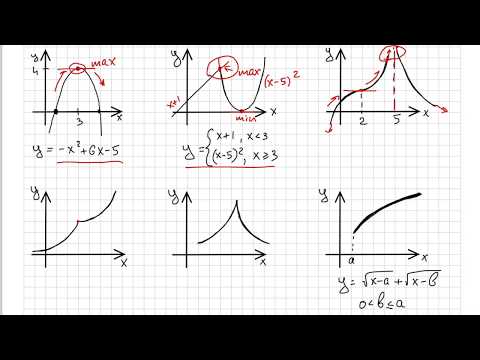
Производная. Часть 10. Экстремумы. Максимум и минимум. Стационарная и критическая. Перегиба и полюс.
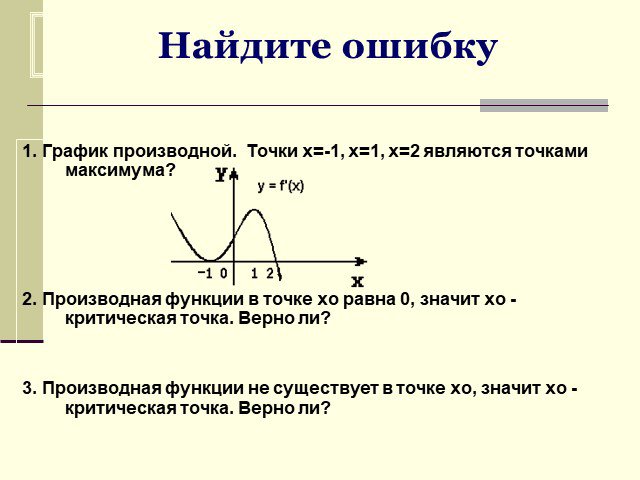
Стационарные точки могут быть максимальными, минимальными или седловыми, в зависимости от того, какой характер имеет в них функция.

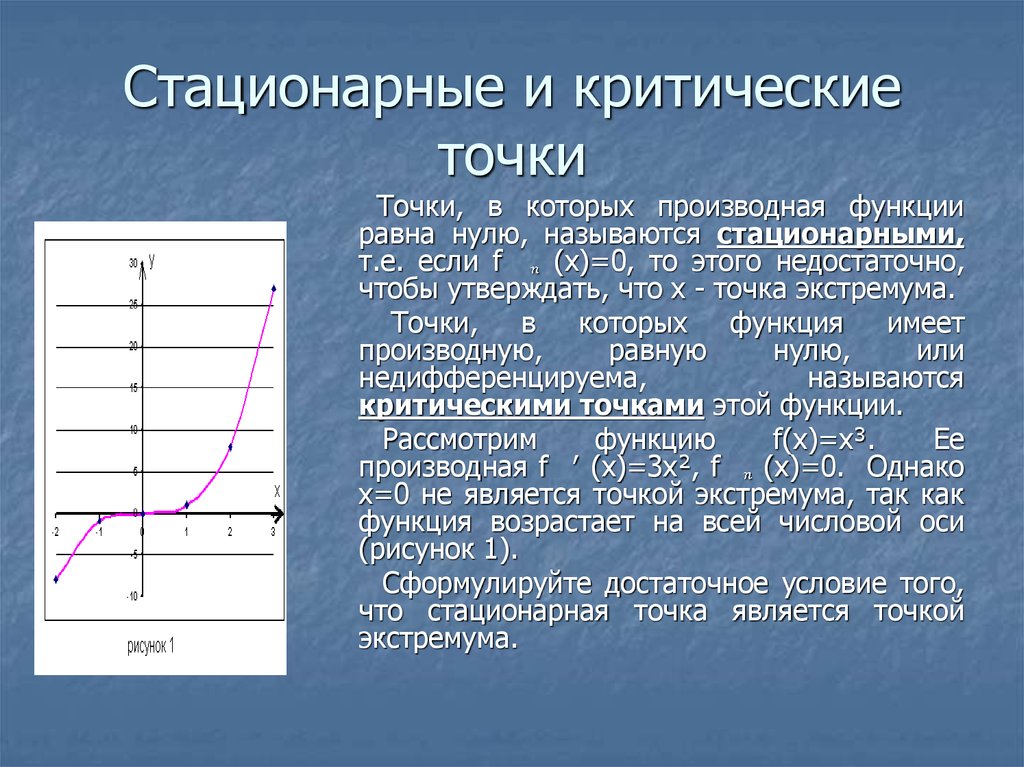
Вторичная производная помогает классифицировать точку экстремума: если она положительна, то точка является минимумом, если отрицательна — максимумом.
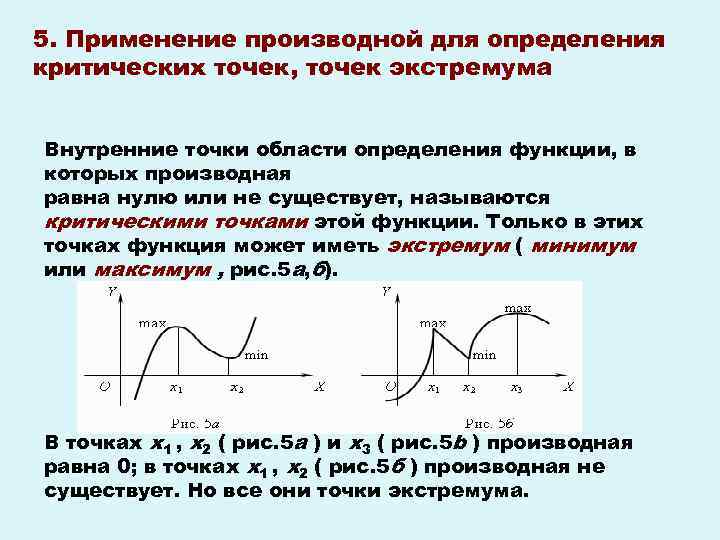
Для нахождения точек экстремума важно не только рассматривать производные, но и учитывать поведение функции в окрестности этих точек.
Исследование функции. Часть 5. Монотонность и экстремумы функции. Минимумы и максимумы
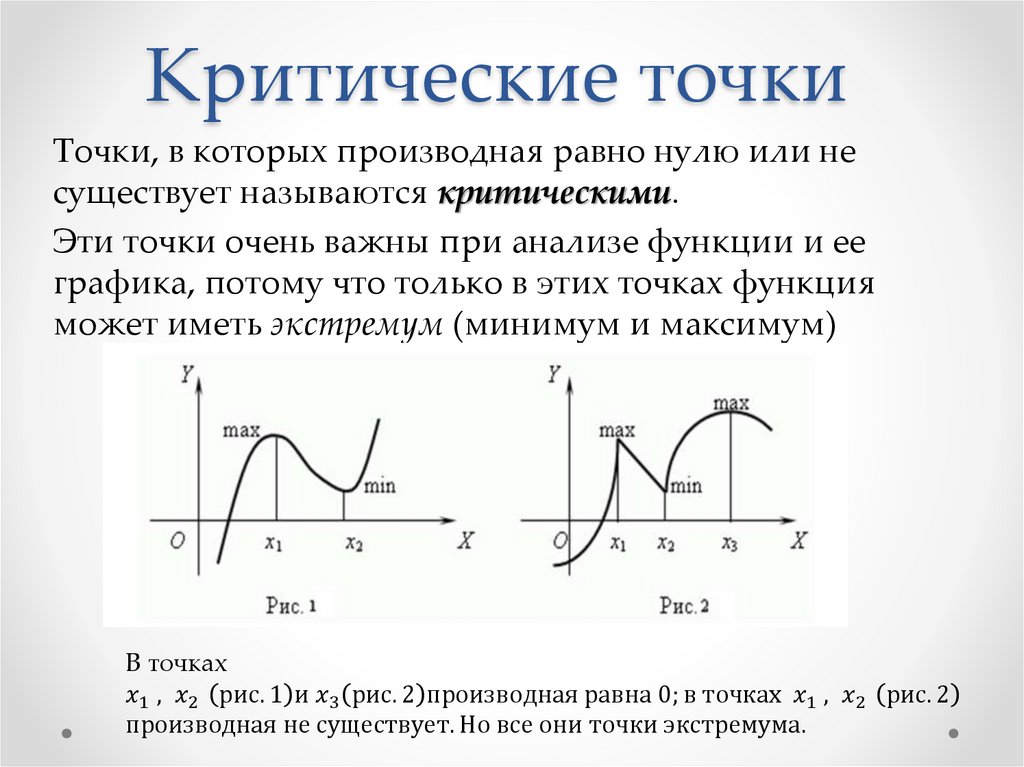
Если на интервале функция непрерывна, то по теореме Ролля между двумя точками с одинаковыми значениями функции обязательно существует стационарная точка.

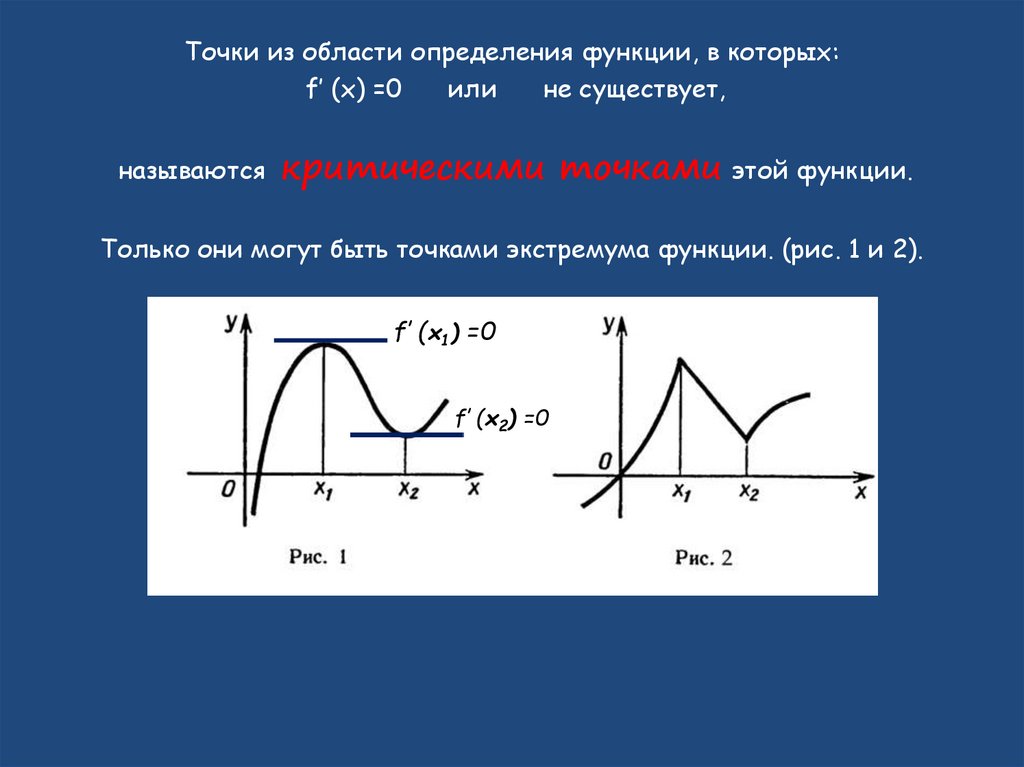
При анализе функции на экстремумы полезно использовать графическое представление, чтобы лучше понять, где могут располагаться критические точки.