Шаги для нахождения уравнения прямой через две точки: простая формула
На данной странице вы найдете подробные инструкции по составлению уравнения прямой, проходящей через две заданные точки на плоскости. Мы разберем, как правильно использовать формулы и шаги, чтобы легко решить задачу.


Для составления уравнения прямой, проходящей через две точки, важно найти её наклон (коэффициент угла), используя формулу: m = (y2 - y1) / (x2 - x1).

Составить уравнение прямой, проходящей через две данные точки. Метод координат. Геометрия 9 класс

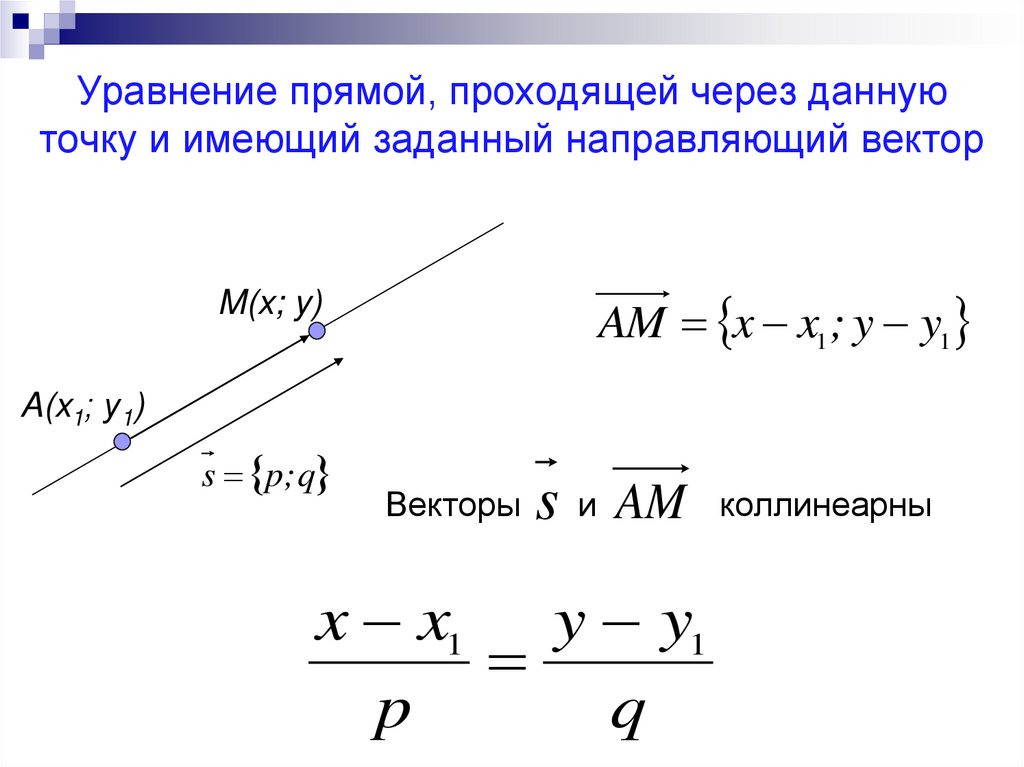
После нахождения наклона, используйте одну из точек для подставления в уравнение прямой в виде y - y1 = m(x - x1).

Составляем уравнение прямой по точкам

Не забывайте, что для вертикальной прямой наклон не существует, и уравнение будет выглядеть как x = const.

Как составить уравнение прямой, проходящей через две точки на плоскости - Математика
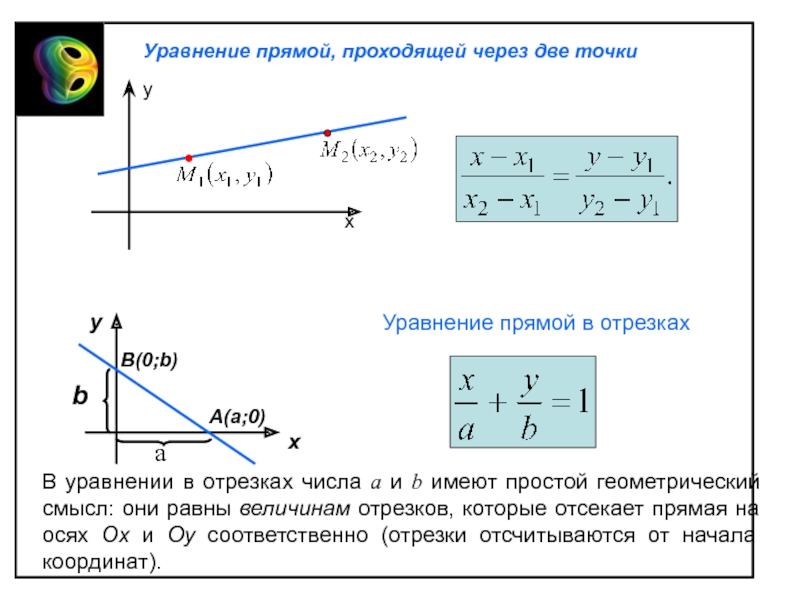
Если точки имеют одинаковую абсциссу, то прямая будет вертикальной, и её уравнение можно записать как x = x1.

Как составить уравнение прямой, проходящей через две точки. Урок 3. Геометрия 8 класс.
Для горизонтальных прямых, у которых одинаковые ординаты, уравнение будет иметь вид y = y1.
Алгебра 7 класс. 26 октября. Составляем уравнение прямой проходящей через заданные точки

Убедитесь, что при подстановке данных в формулу вы правильно учли знаки разностей координат точек.


Если уравнение полученное в результате, не соответствует вашим ожиданиям, проверьте вычисления наклона.

Метод координат Урок №2 2 Нахождение уравнения плоскости по трем точкам

Для упрощения вычислений используйте калькулятор, если точки имеют большие или дробные координаты.
Записать уравнение прямой, проходящей через известные точки

Обратите внимание, что точность в вычислениях важна для получения правильного уравнения прямой.


Практикуйтесь с разными парами точек, чтобы лучше понять процесс составления уравнений прямых и быстрее решать подобные задачи.
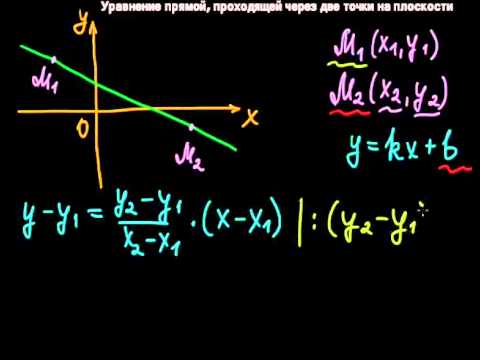
§11 Уравнение прямой, проходящей через две точки на плоскости