Способы задания соответствия между двумя множествами и их ключевые особенности

Этот раздел посвящен основным методам задания соответствия между двумя множествами. Здесь вы найдете полезные советы и примеры, которые помогут лучше понять, как корректно строить такие соответствия, какие существуют подходы и как их применять в различных областях, включая математику, информатику и логику.

При задании соответствия между множествами важно точно определить, какие элементы из одного множества сопоставляются с элементами другого множества.

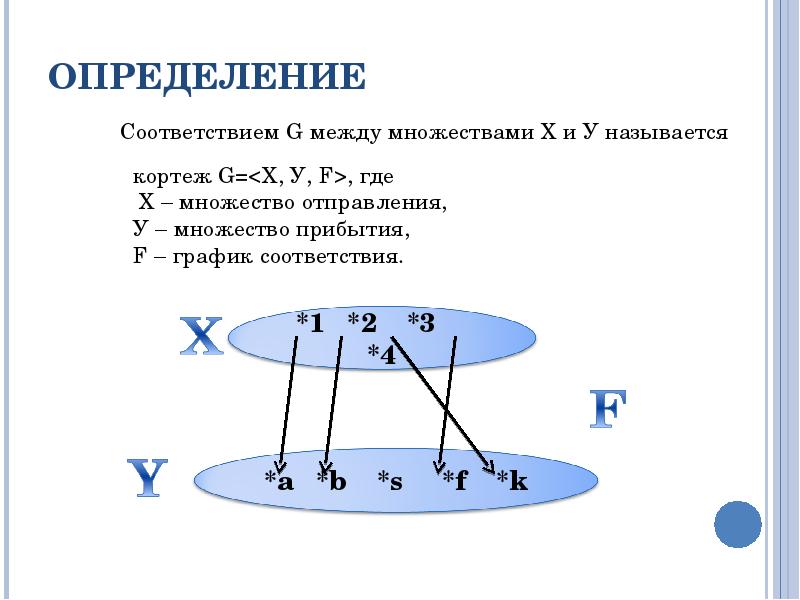
Используйте таблицы или диаграммы Венна для визуализации соответствий и наглядного представления отношений между множествами.

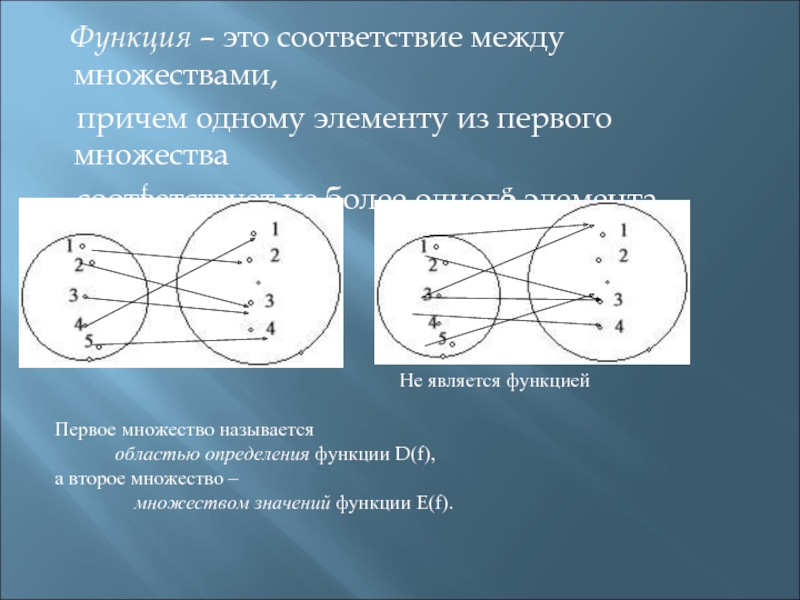
В случае бесконечных множеств используйте кардинальные числа и понятия из теории множеств для задания соответствий.

Задание соответствия через функции или отображения помогает формализовать отношение между элементами двух множеств.

Если множества имеют различные кардинальности, используйте методы сравнения их мощностей, такие как биекция или инъекция.

Для отображений между множествами важно определить, является ли соответствие взаимно однозначным или допускает многозначные соответствия.

Когда работа с множествами связана с базами данных, важно учесть ключевые поля, чтобы корректно задать связи между записями.

Для простоты вычислений и анализа лучше использовать стандартные алгоритмы и формулы для построения соответствий в алгебре и теории графов.

Иногда для задания соответствий может быть полезно использование структур данных, таких как массивы, списки или хеш-таблицы.

Проверяйте корректность соответствия, используя методы математической индукции или доказательства от противного, чтобы убедиться в точности вашего подхода.