Методы и подходы к анализу событий на диаграммах Эйлера
Диаграммы Эйлера — это мощный инструмент для визуализации взаимосвязей между различными событиями и объектами. В этой подборке вы найдете полезные советы по созданию, интерпретации и применению диаграмм Эйлера для различных задач, от теоретических исследований до практических приложений. Каждое событие можно изобразить в виде множества, а их пересечения — наглядно представить с помощью диаграмм для лучшего понимания их взаимосвязей.

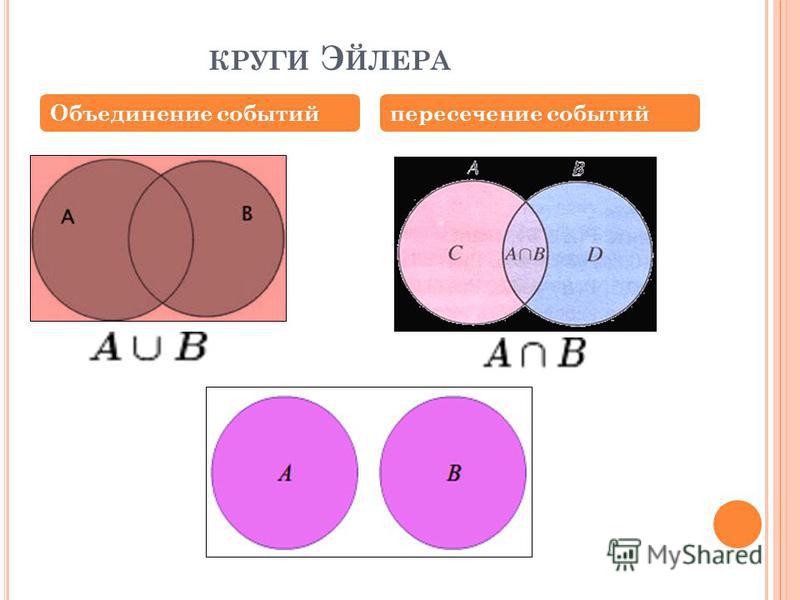
Для корректной визуализации событий на диаграмме Эйлера важно правильно выбрать универсальные множества, отражающие все возможные исходы.

Подмножество. Операции над множествами (пересечение, объединение множеств) – 8 класс алгебра
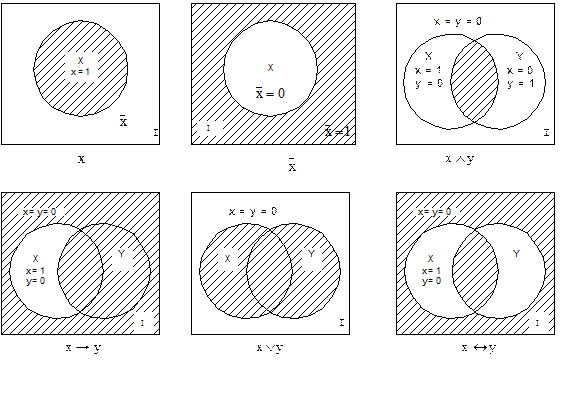
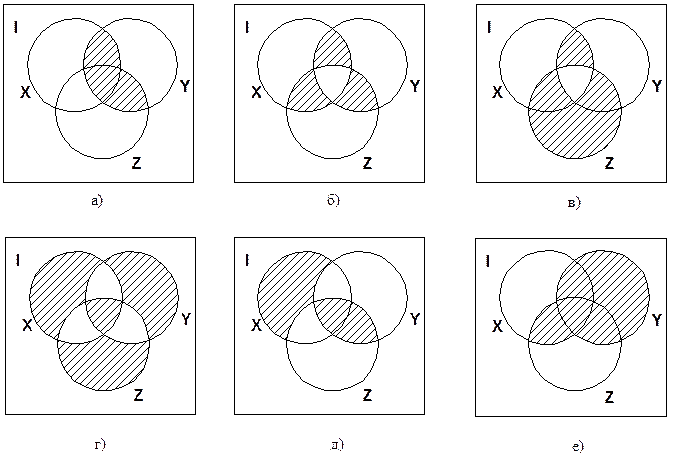
Убедитесь, что диаграмма отражает все возможные пересечения между множествами, чтобы не упустить важные взаимосвязи.

Операции над событиями на кругах Эйлера
Используйте разные цвета для выделения пересечений на диаграмме, чтобы улучшить восприятие и облегчить анализ данных.

Самый короткий тест на интеллект Задача Массачусетского профессора
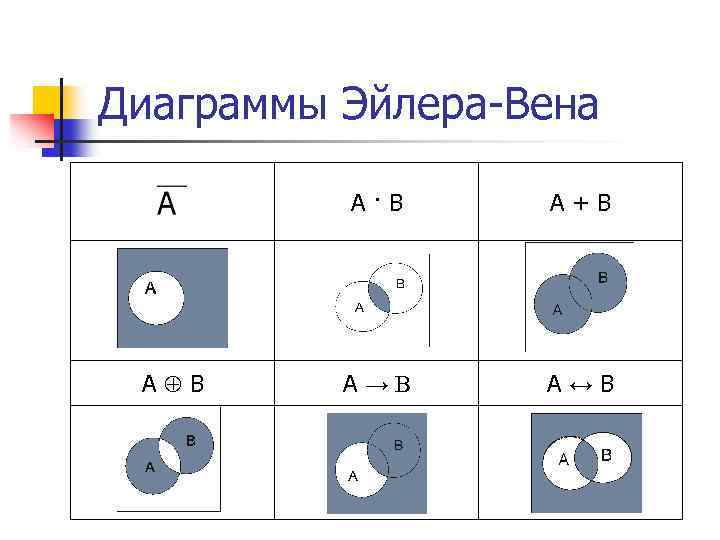
Для более сложных данных можно использовать многомерные диаграммы Эйлера, включая несколько слоев и дополнительных осей.

Профильный ЕГЭ 2025. Задание 4. Условная вероятность. Изменения 2023.
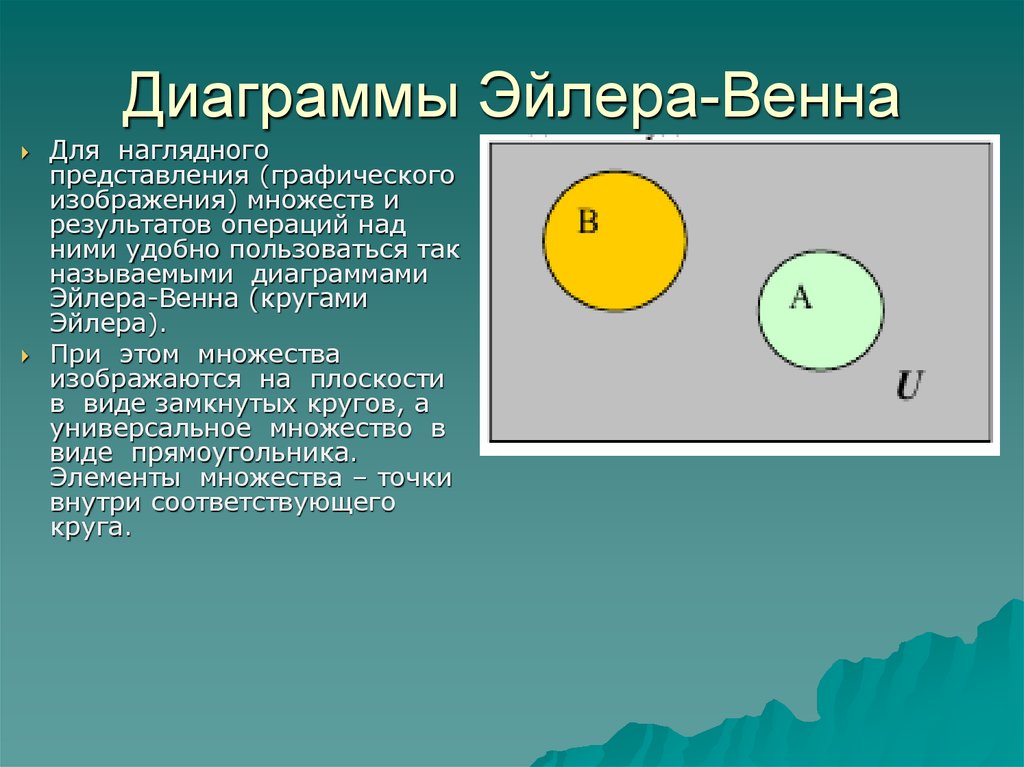
Всегда следите за тем, чтобы диаграмма была ясной и не перегружена информацией, иначе она потеряет свою информативность.

Пересечение и объединение множеств. Алгебра, 8 класс
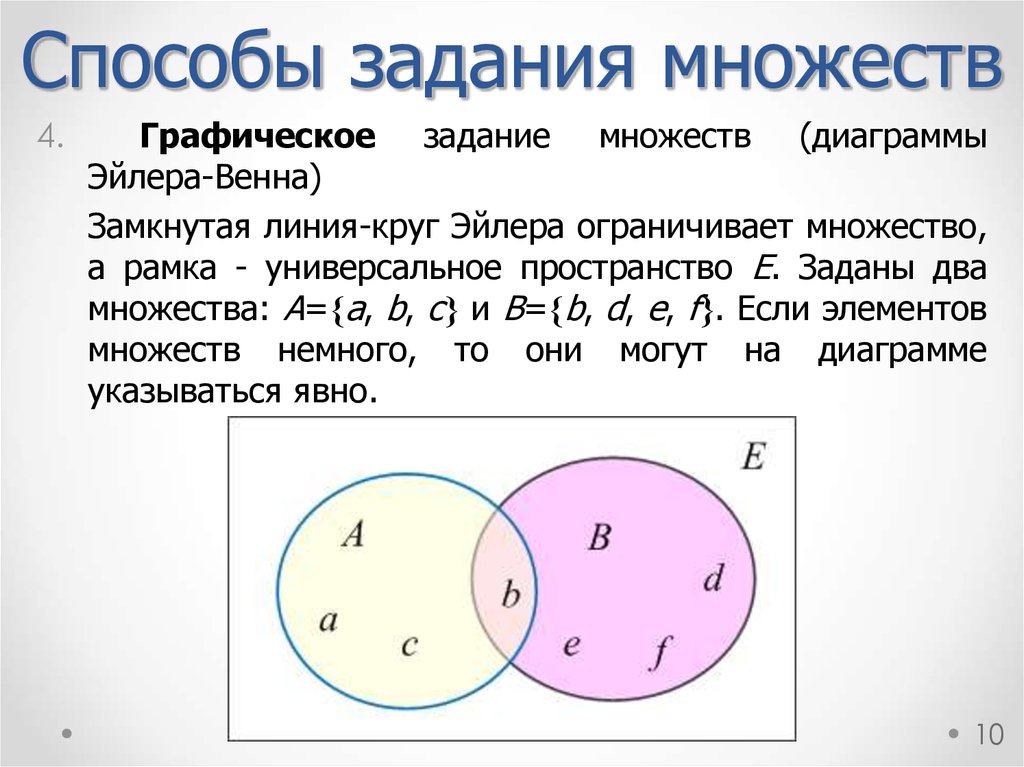
Применяйте диаграммы Эйлера не только в теоретических задачах, но и для практических решений, например, для анализа рисков или оптимизации процессов.

Логика - Диаграммы (круги) Эйлера-Венна. Разбор задач
Диаграммы Эйлера могут быть полезны в различных областях, таких как логика, теория вероятностей, биология и социология.
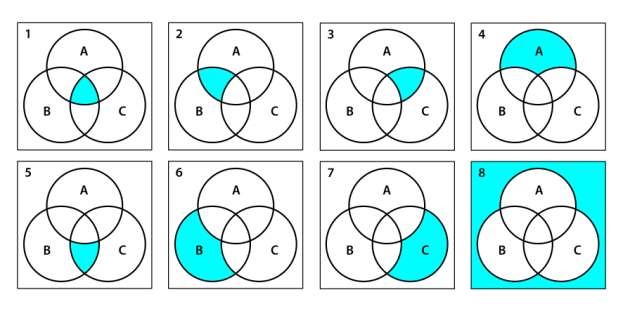

Перед тем как создавать диаграмму, тщательно продумайте, какие события и их пересечения должны быть изображены для максимальной наглядности.

Используйте диаграммы Эйлера, чтобы моделировать различные сценарии и предсказывать возможные исходы на основе существующих данных.

Введение в теорию вероятности. Диаграмма Венна.
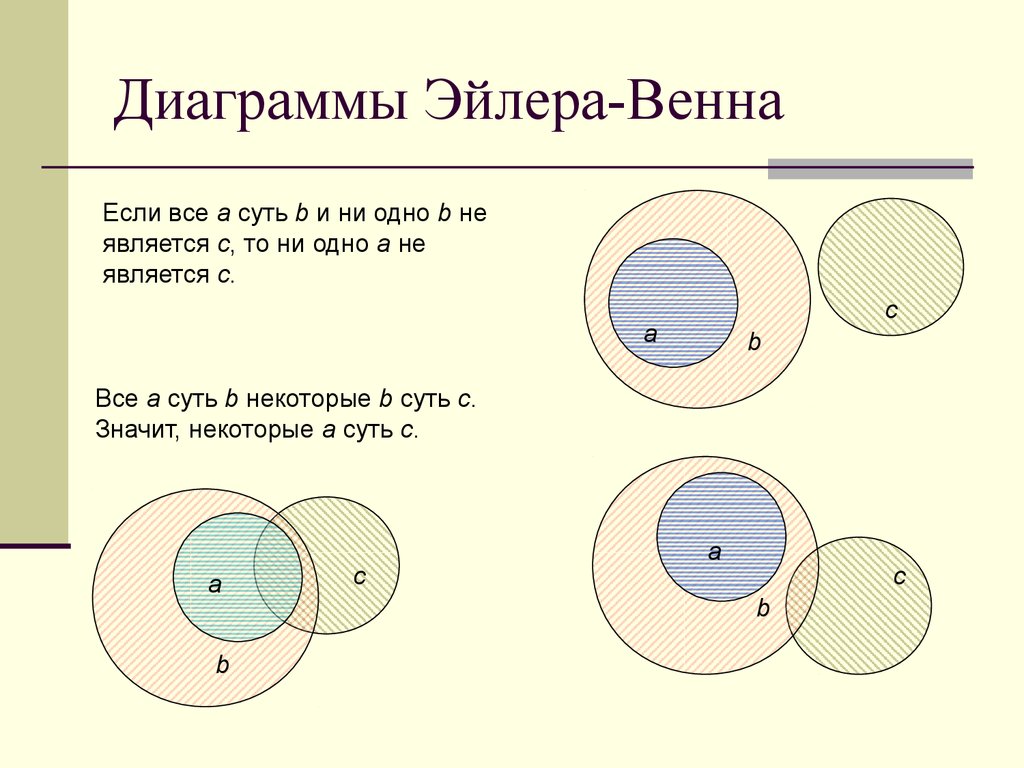
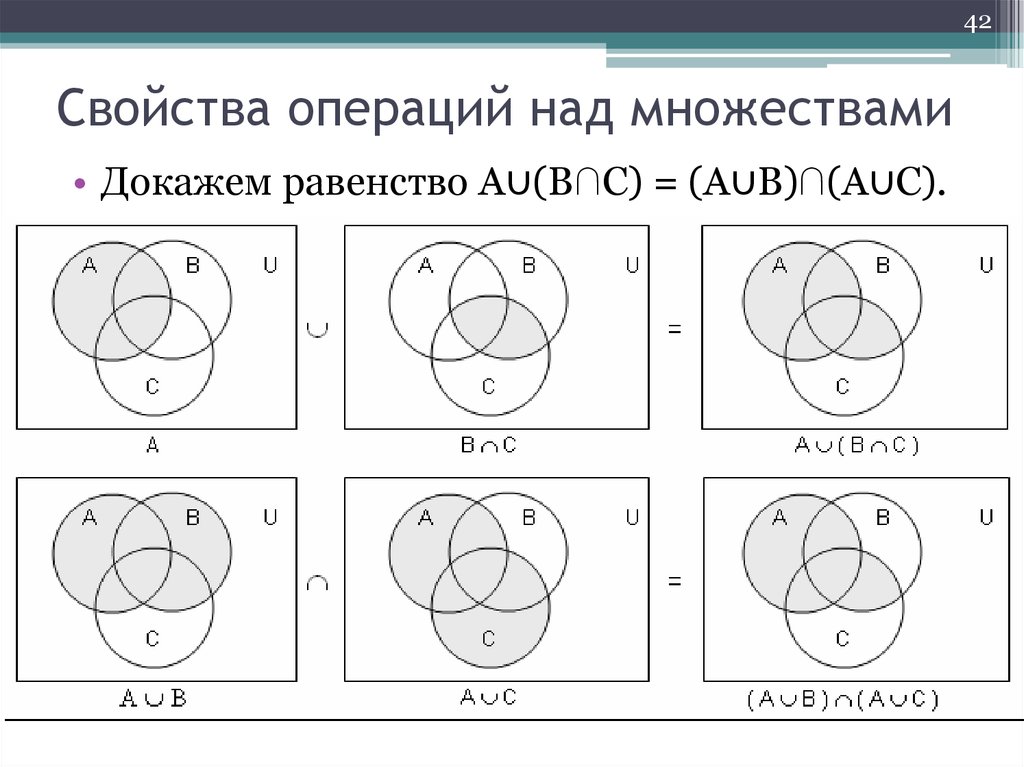
Диаграммы Эйлера также могут быть полезны для решения задач с ограничениями, где необходимо учесть пересечения множества условий или требований.
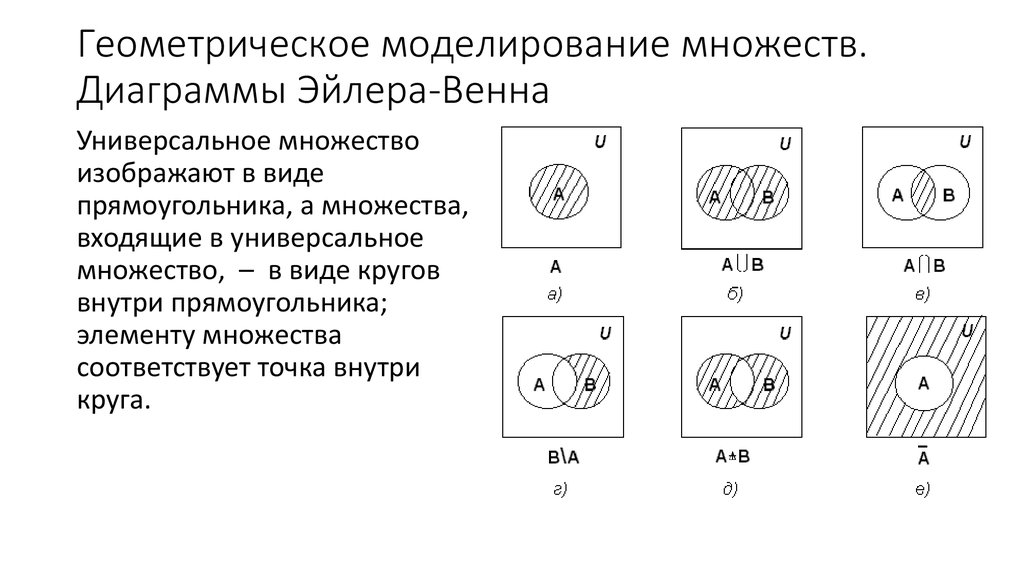
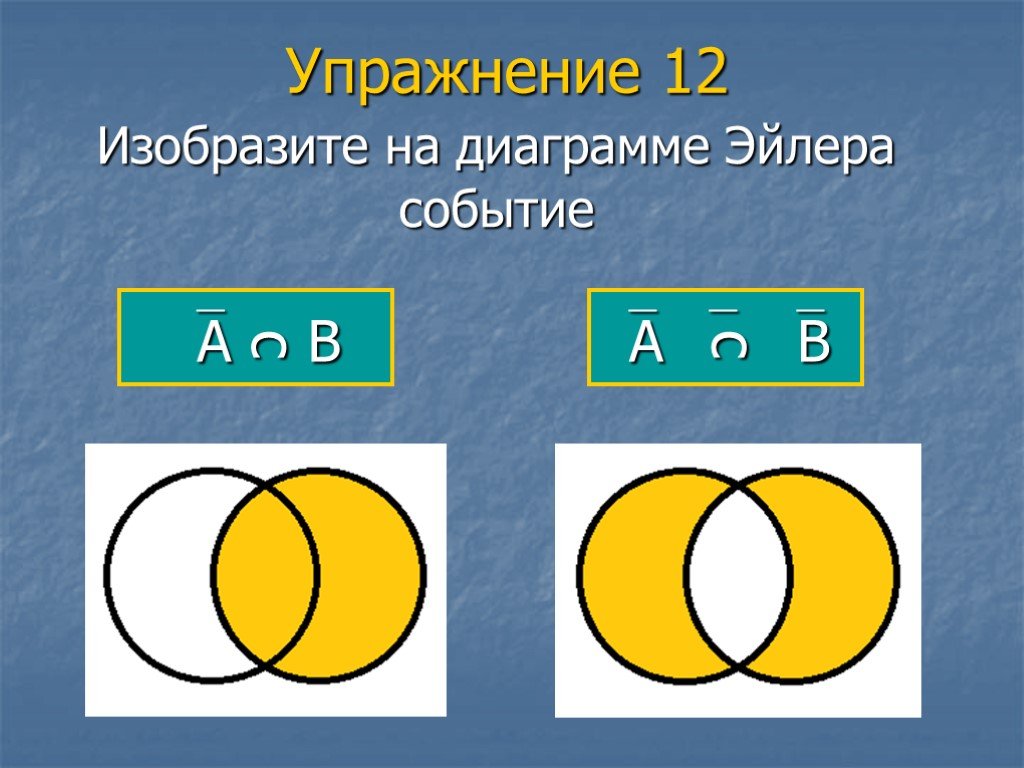

8. Противоположные события. Диаграммы Эйлера.