Скорость и ускорение через производные: ключевые понятия и советы

Скорость и ускорение — важнейшие концепции физики, которые часто выражаются через производные. В этой статье мы подробно рассмотрим, как использовать производные для нахождения этих величин, а также дадим полезные советы по их правильному применению в решении задач.

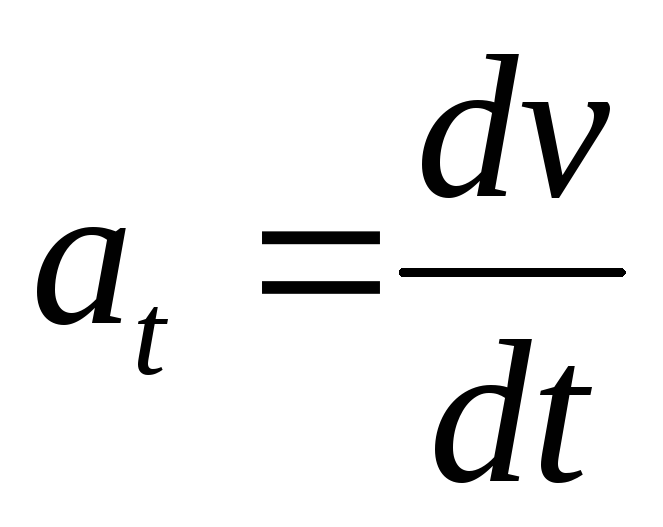
Для вычисления скорости используйте первую производную положения по времени.

Ускорение вычисляется через вторую производную положения по времени или первую производную скорости.

Если положение объекта задано функцией, его скорость и ускорение можно найти, дифференцируя эту функцию.

Будьте внимательны при анализе графиков: скорость — это наклон графика положения, а ускорение — наклон графика скорости.

Используйте правила дифференцирования для сложных функций, например, для полиномиальных и тригонометрических выражений.

Не забывайте учитывать единицы измерения: скорость в метрах в секунду, ускорение в метрах на секунду в квадрате.

Когда скорость постоянна, ускорение равно нулю, это помогает упростить расчеты.

В задачах с переменной скоростью часто важно учитывать её изменение по времени для точных расчетов ускорения.

Понимание разницы между мгновенной и средней скоростью поможет избежать ошибок при вычислениях.

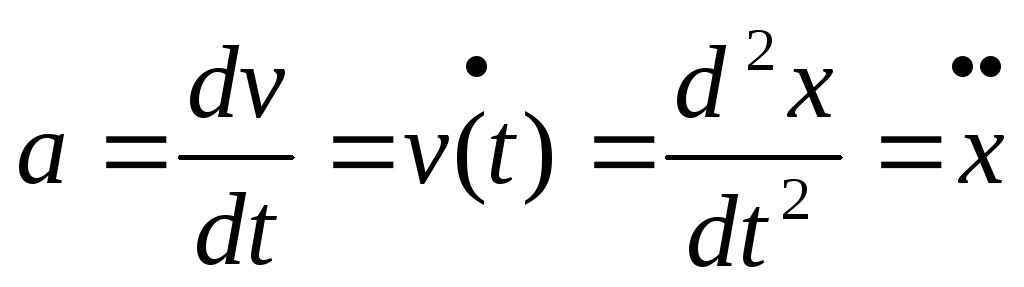
Для сложных задач используйте графики и визуализацию: это помогает наглядно представить зависимость скорости и ускорения от времени.