Решение системы нормальных уравнений гиперболы: ключевые подходы и советы
На этой странице представлены полезные советы и рекомендации по решению системы нормальных уравнений гиперболы. Данные методы являются основой для построения и анализа гиперболических кривых в аналитической геометрии, что позволяет точно и быстро находить их уравнения и характеристики.
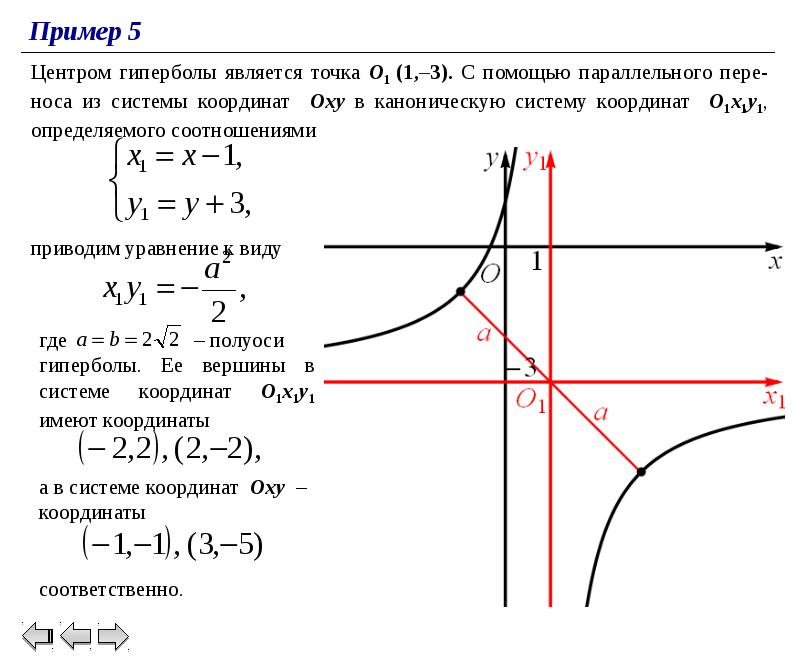


Для решения системы нормальных уравнений гиперболы важно правильно определить координаты её фокусов и асимптот.
Гипербола. Функция k/x и её график


Не забывайте, что гипербола имеет два фокуса, и их расположение сильно влияет на форму кривой.
функция y=k/x и ее график (гипербола) - 8 класс алгебра
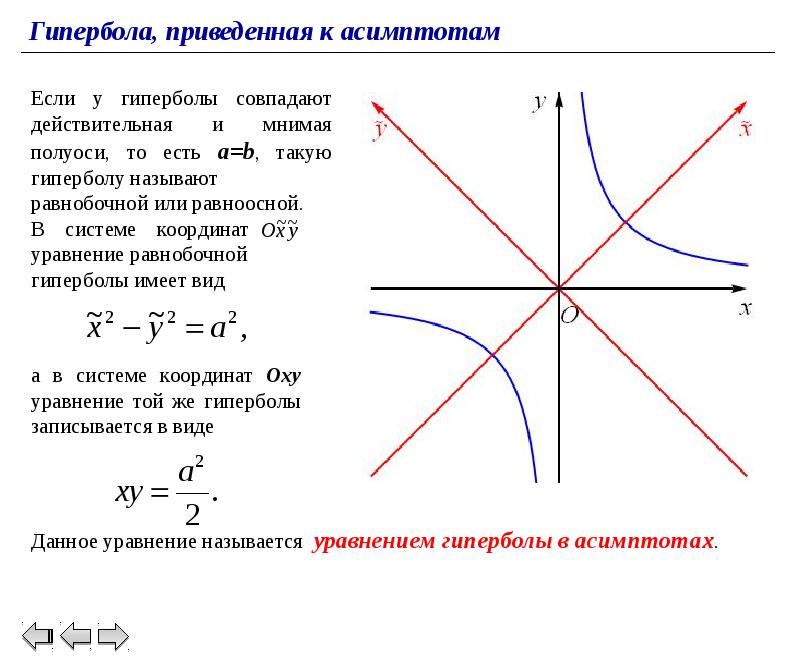
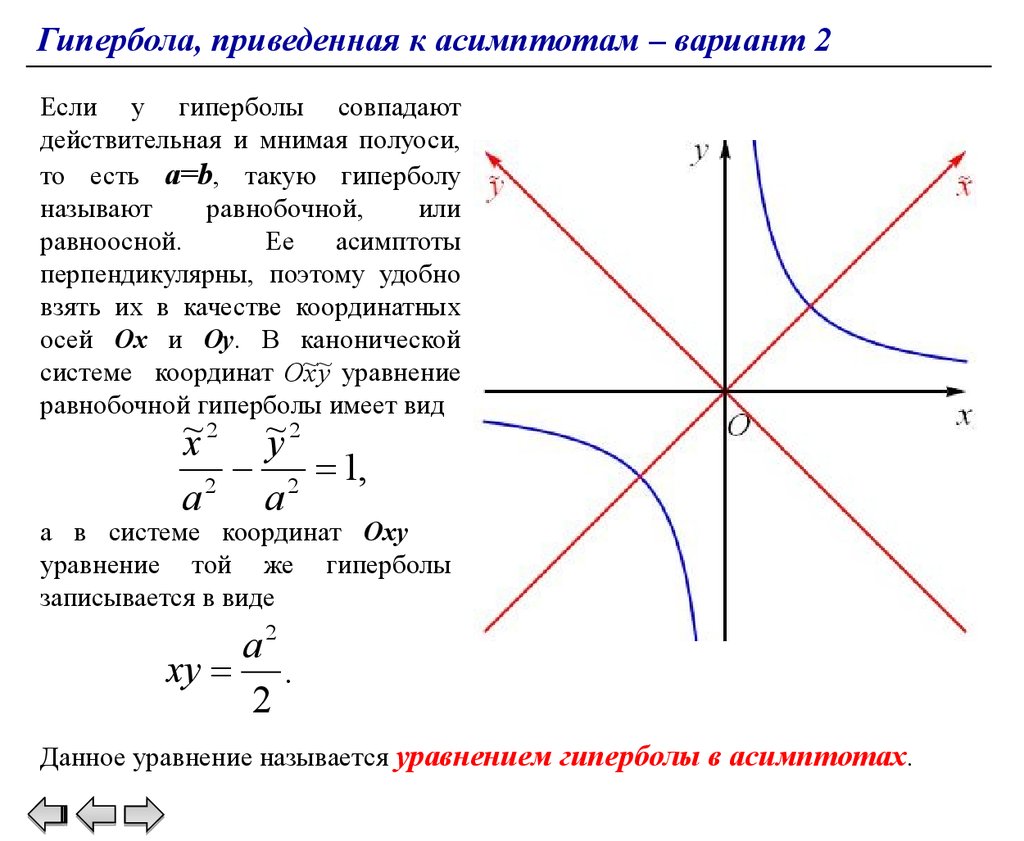
Использование параметрического представления гиперболы может значительно упростить решение системы уравнений.
✓ Гипербола - Ботай со мной #142 - Борис Трушин
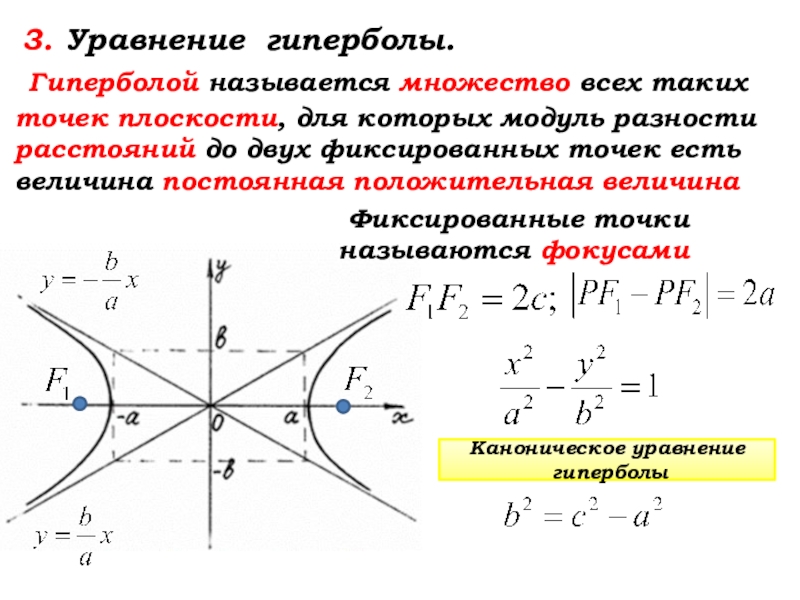
Для более точных вычислений всегда проверяйте знак коэффициентов в уравнении гиперболы.

Гипербола со смещением

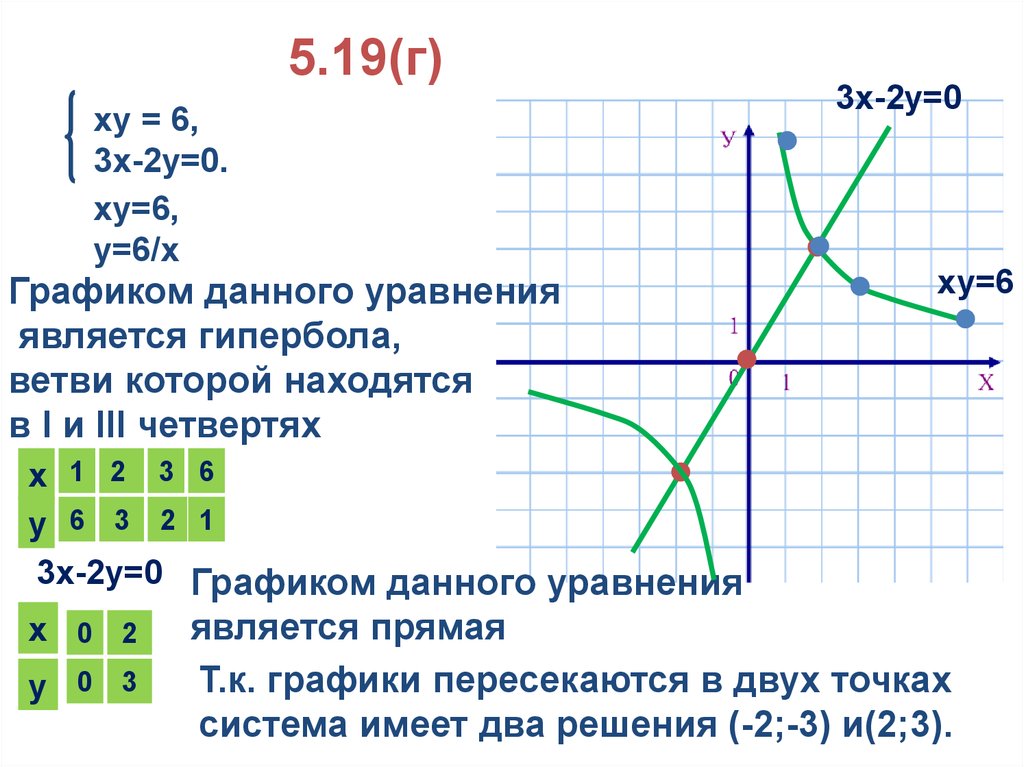
Не забывайте учитывать асимптоты гиперболы, которые можно найти через систему нормальных уравнений.

Приведение гиперболы к каноническому виду: поворот, построение


Практика с примерами поможет глубже понять и освоить методы решения таких систем.

График – гипербола. Находим коэффициенты в формуле
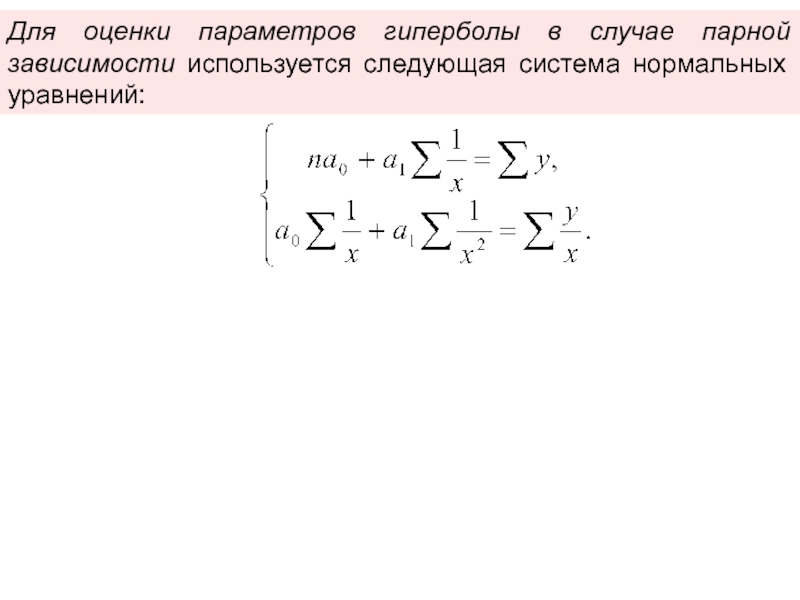
Решение системы нормальных уравнений требует аккуратности при использовании методов подстановки и исключения переменных.


При работе с гиперболами всегда проверяйте их характер и расположение относительно осей координат.
Помните, что система нормальных уравнений может быть решена как аналитически, так и численно, в зависимости от конкретной задачи.
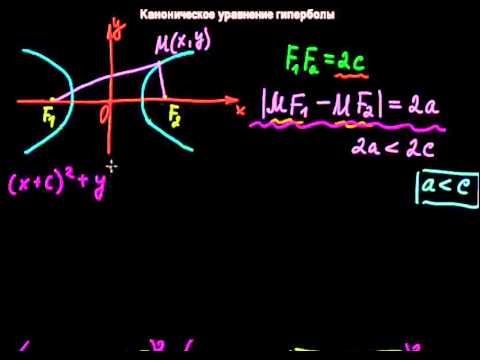
§21 Каноническое уравнение гиперболы

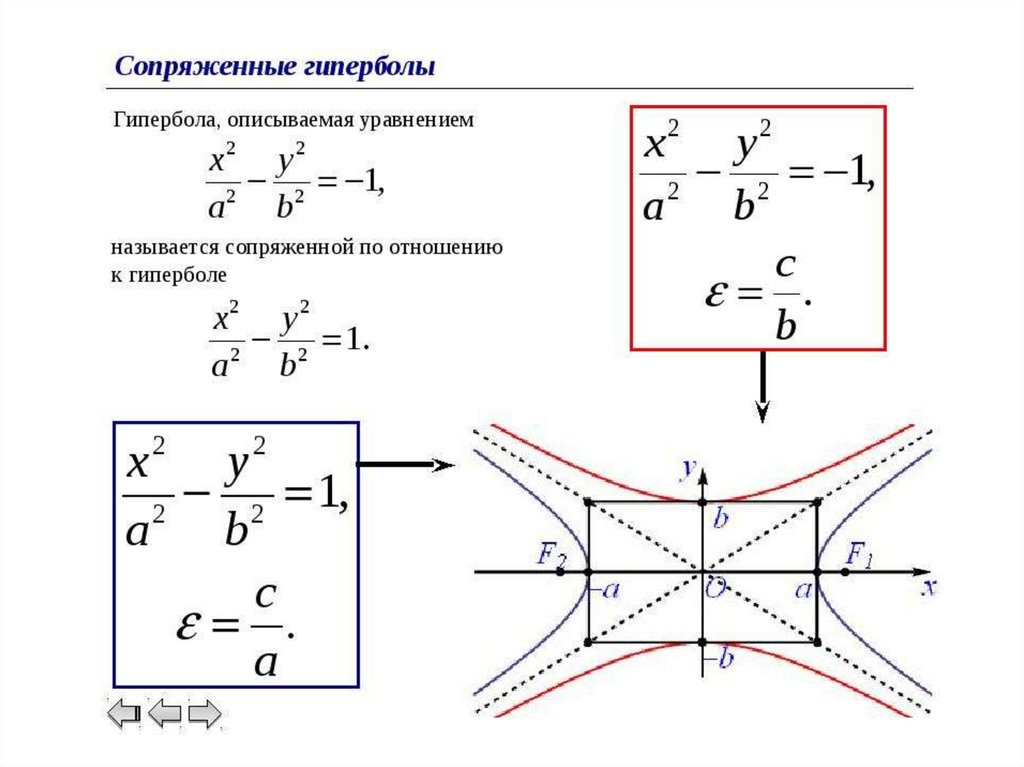
Для лучшего усвоения материала полезно изучать графические интерпретации гиперболы и её уравнений.
Уравнение с параметром #6 (Модуль гиперболы) ЕГЭ №501070

