Как решить систему уравнений методом подстановки: три различных подхода
Метод подстановки является одним из самых популярных способов решения систем линейных уравнений. На этой странице мы рассмотрим три различных подхода к решению таких систем, поделимся полезными советами и дадим подробные инструкции для успешного освоения этого метода. Вы сможете легко разобраться в алгоритме подстановки и применить его на практике для решения разнообразных задач.
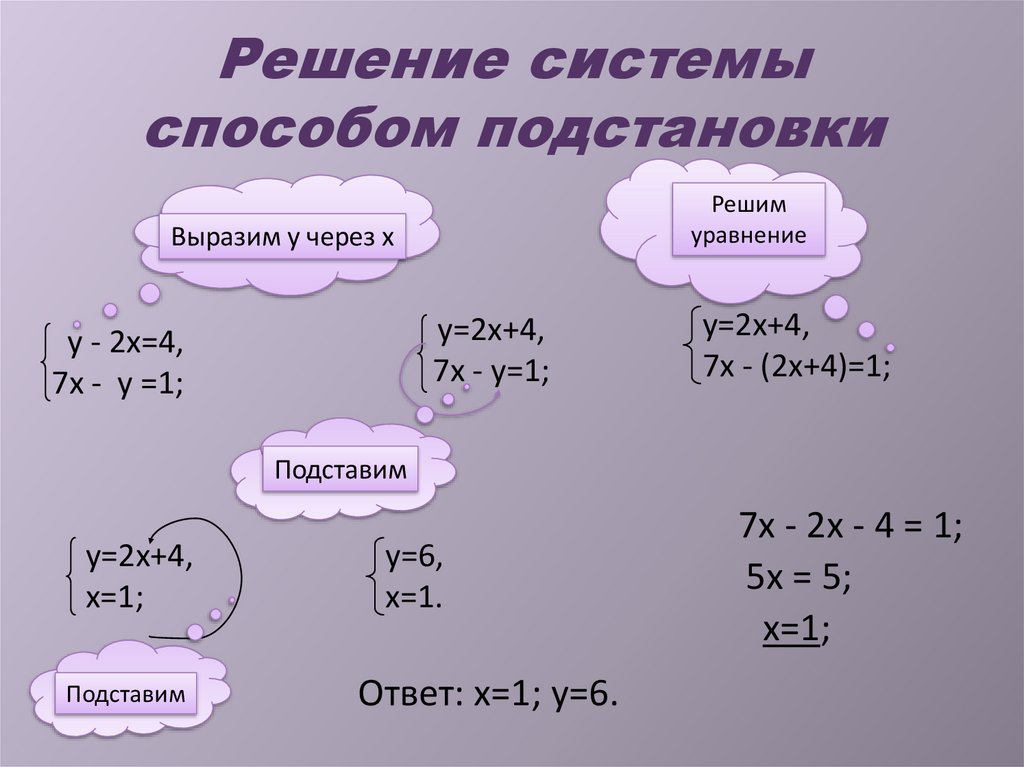
Перед началом решения системы убедитесь, что уравнения находятся в стандартной форме: Ax + By = C, где A, B, C - числовые коэффициенты.
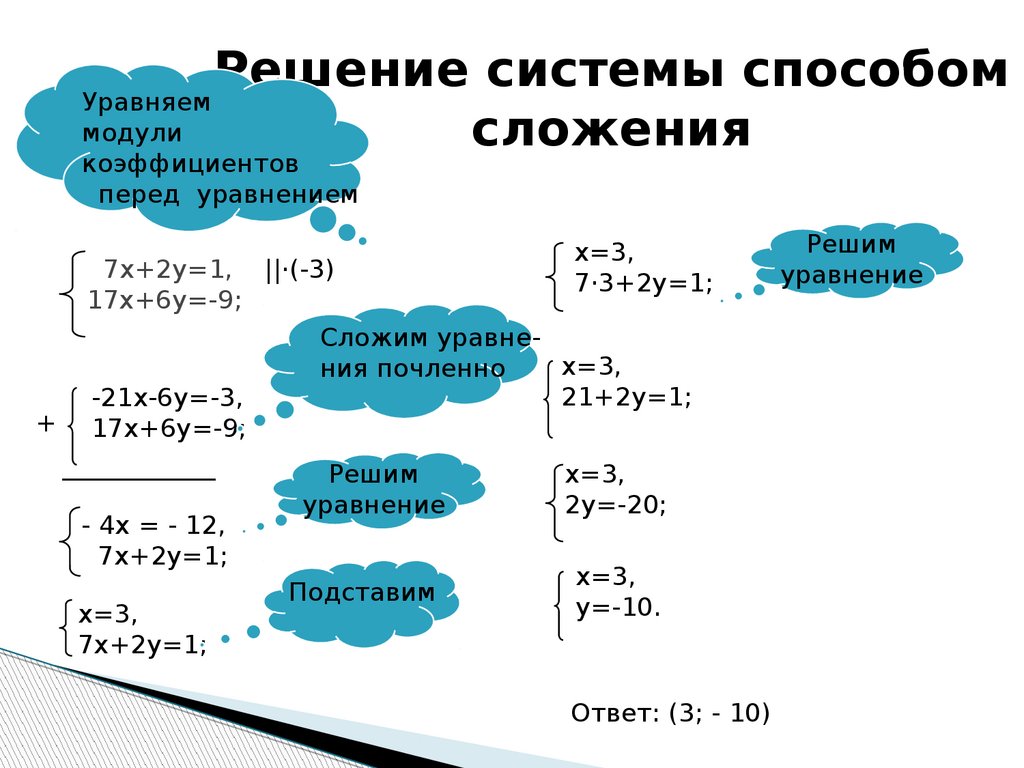
Решение систем уравнений методом сложения

Если в одном из уравнений уже выражена одна переменная через другую, начните с подстановки этого выражения в другое уравнение.

Алгебра 7 класс. Решение систем уравнений методом подстановки

При решении методом подстановки важно внимательно следить за знаками при перемещении слагаемых.
Решение систем уравнений методом подстановки
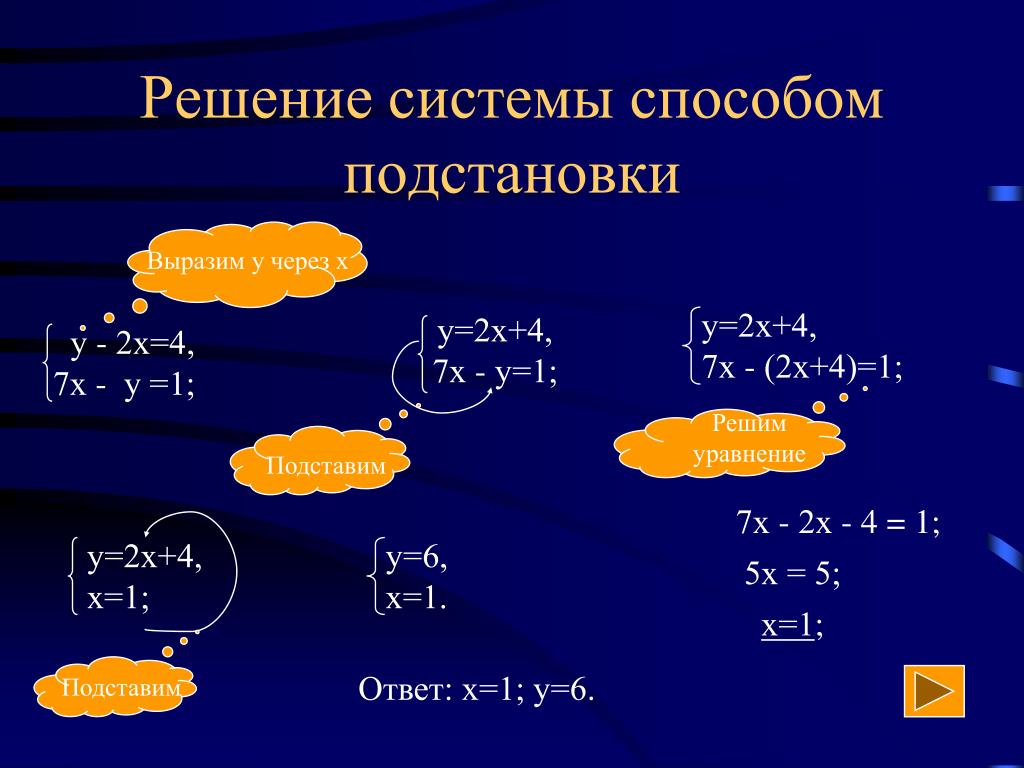
Если у вас не получается выразить одну переменную через другую, попробуйте умножить уравнение на число, чтобы избавиться от дробей или сделать коэффициенты более удобными для подстановки.

Самый короткий тест на интеллект Задача Массачусетского профессора

Проверяйте свои результаты после подстановки в исходные уравнения, чтобы убедиться в правильности решения.

Системы линейных уравнений с двумя неизвестными. Способ постановки или железобетонный метод, 7 класс


Если система уравнений имеет бесконечно много решений, проверьте, не являются ли уравнения тождественно равными.
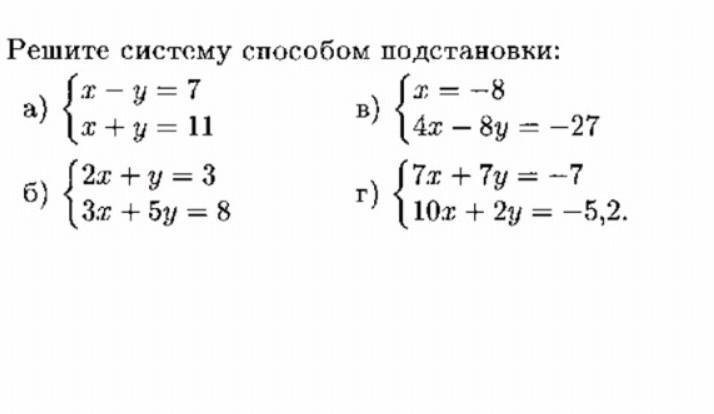
Не забывайте о возможности появления ошибок при подстановке, таких как неправильное сложение или вычитание. Рекомендуется делать промежуточные проверки.


Когда найдете одно значение переменной, подставьте его обратно в уравнение, чтобы найти второе значение переменной.
Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.


Для систем с дробными коэффициентами удобно умножить оба уравнения на наименьшее общее кратное знаменателей перед подстановкой.

Реакция на результаты ЕГЭ 2022 по русскому языку


После нахождения решения системы всегда записывайте окончательный ответ в виде пары значений, соответствующих переменным x и y, если это система двух переменных.

