Рассчитываем радиус описанной сферы для правильных призм: советы и рекомендации
Радиус сферы, описанной около призмы, является важным элементом при решении задач геометрии. Этот показатель позволяет понять, как правильно можно вписать сферу вокруг призмы, а также используется для различных инженерных и научных расчетов. В этой статье представлены полезные советы по вычислению радиуса и особенностей правильных призм, что поможет вам разобраться в этом процессе.

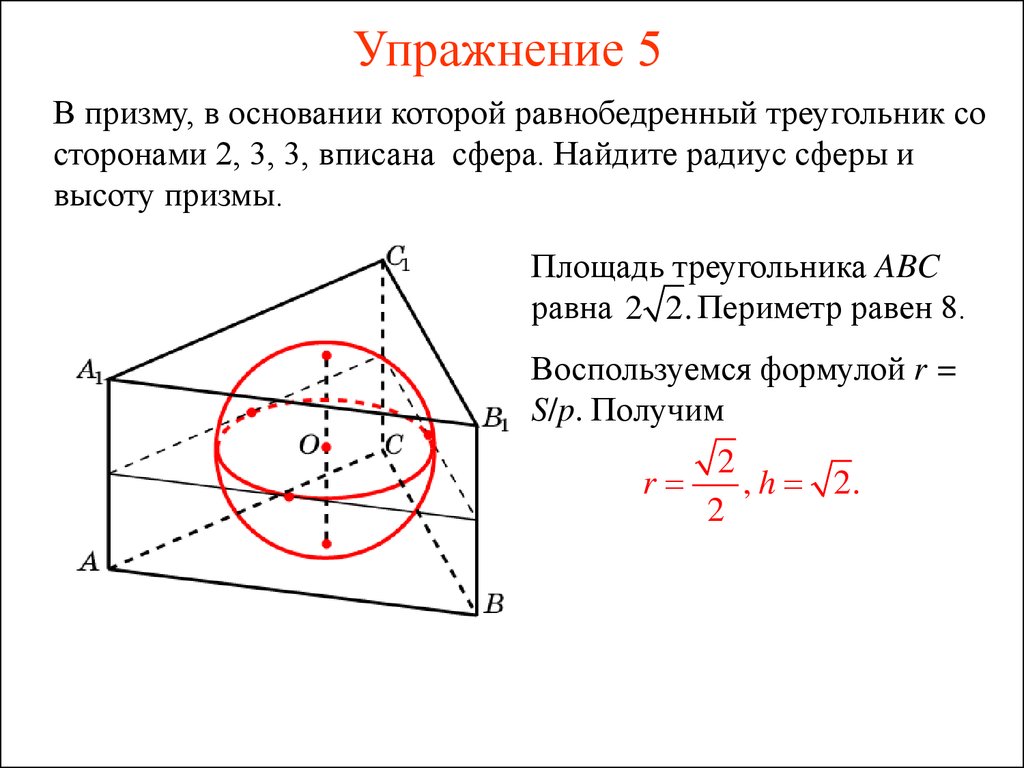
Для расчета радиуса сферы, описанной около призмы, важно учитывать, что он равен расстоянию от центра оснований до вершины самой высокой точки призмы.

Быстро находим радиус описанной сферы
При вычислении радиуса описанной сферы для правильной призмы, учитывайте, что радиус сферы всегда будет равен радиусу описанной окружности основания призмы.

ЕГЭ Задание 14 Пирамида вписана в сферу
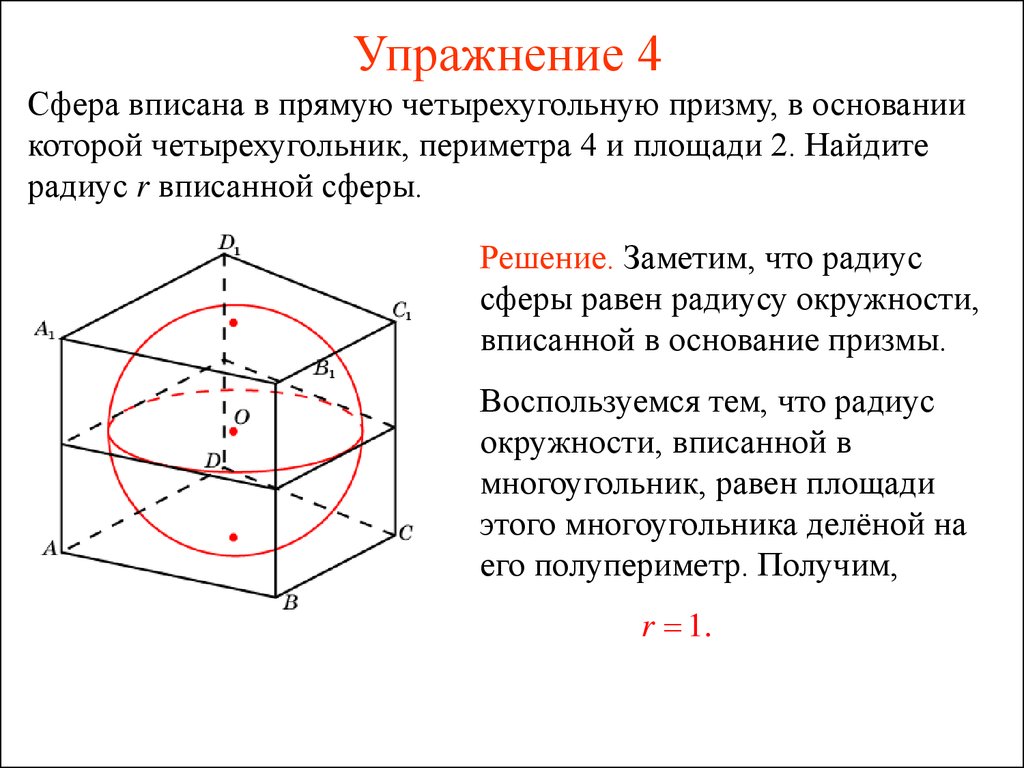
В задачах на радиус описанной сферы важно помнить, что правильная призма обладает одинаковыми углами между соседними гранями.
Найти радиус описанной сферы около пирамиды Д213
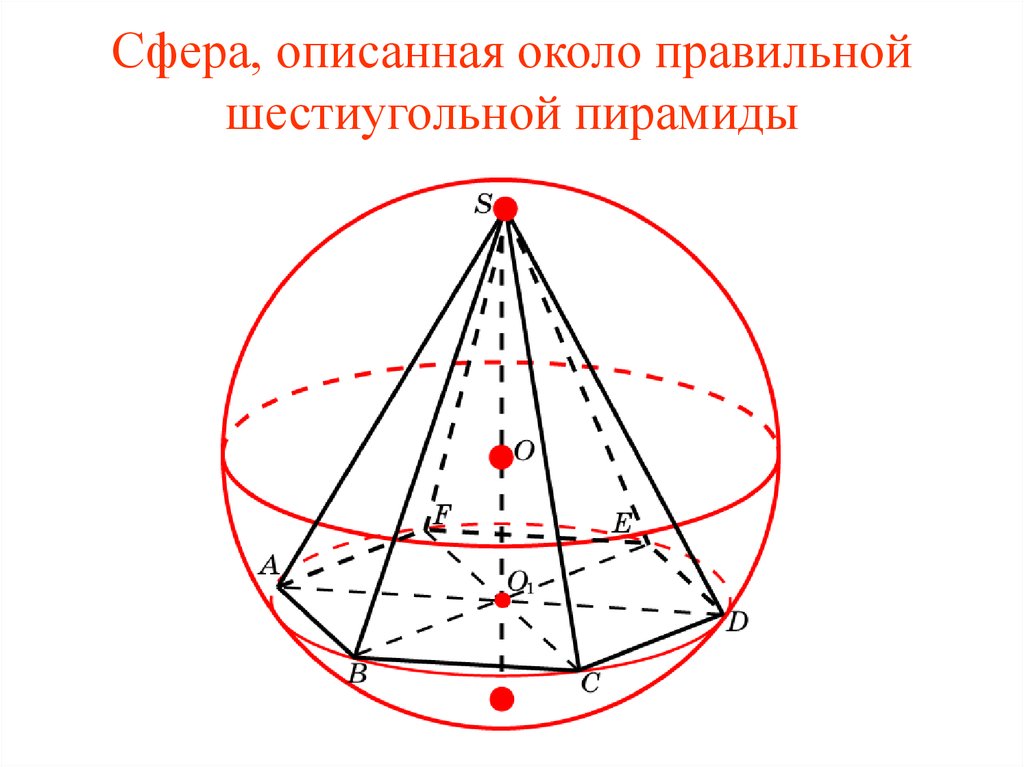
Для правильных многоугольных оснований правильной призмы радиус описанной сферы равен расстоянию от центра основания до вершины перпендикулярно оси симметрии.

5.2. Многогранник, описанный вокруг сферы.
Обратите внимание, что для вычисления радиуса сферы часто необходимо использовать формулы для высоты призмы и её оснований.

Призма, вписанная в шар. Prism, inscribed in a ball.
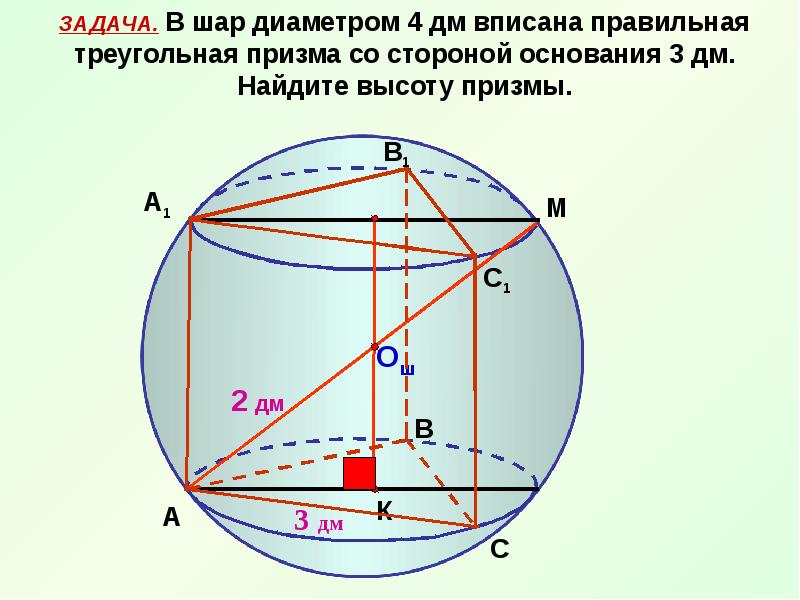
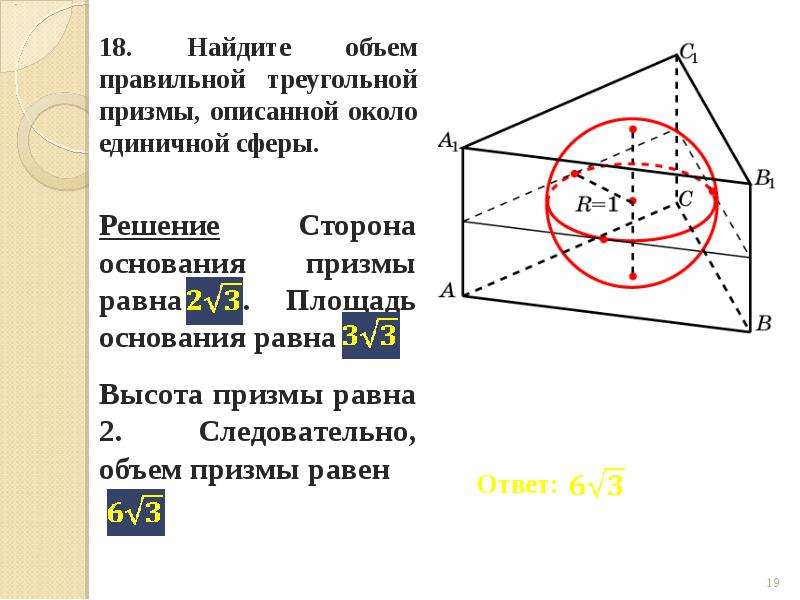
Часто для нахождения радиуса описанной сферы используют соотношение между длиной стороны основания и высотой призмы.
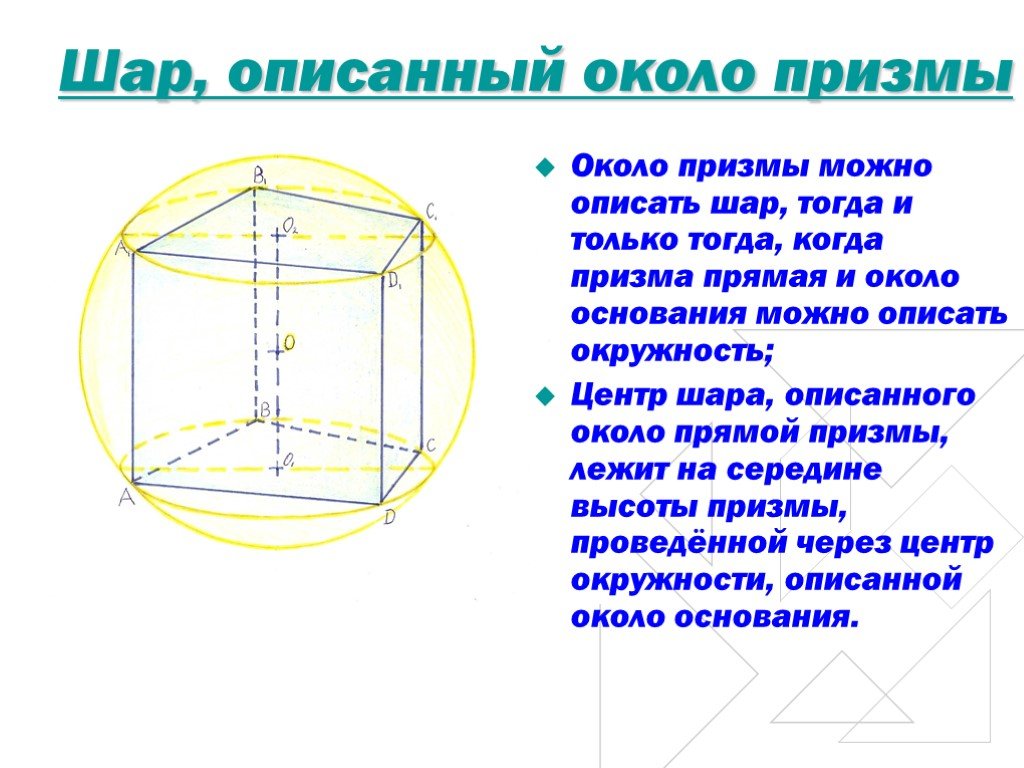
Не забывайте, что для цилиндрических призм радиус сферы будет одинаков с радиусом основания, если призма является правильной.

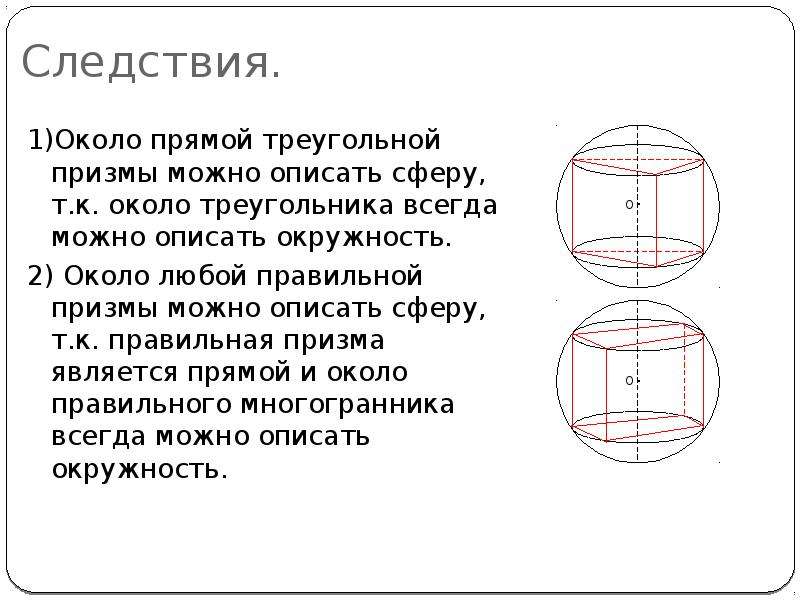
Призма, описанная около шара, или шар, вписанный в призму.
Если призма имеет основание в виде правильного многоугольника, то радиус описанной сферы может быть найден через апофему этого многоугольника.
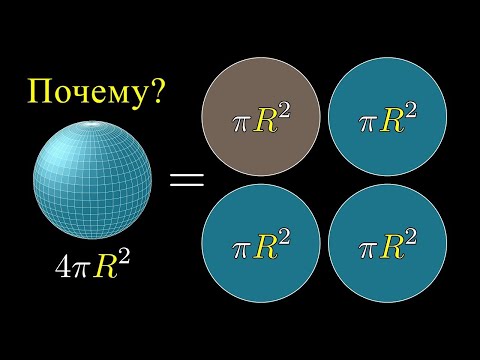
Почему площадь сферы в четыре раза больше её тени? [3Blue1Brown]

ЕГЭ Задание 14 Пирамида Сфера
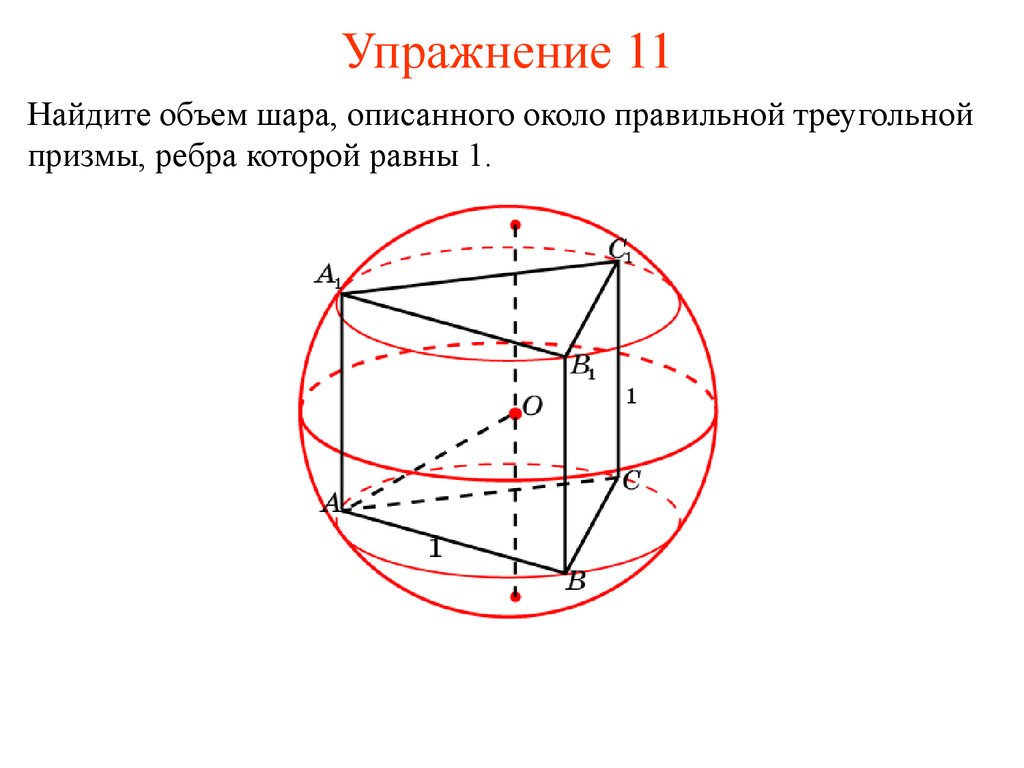
Понимание геометрических свойств правильной призмы и её окружности критически важно для точных вычислений радиуса описанной сферы.
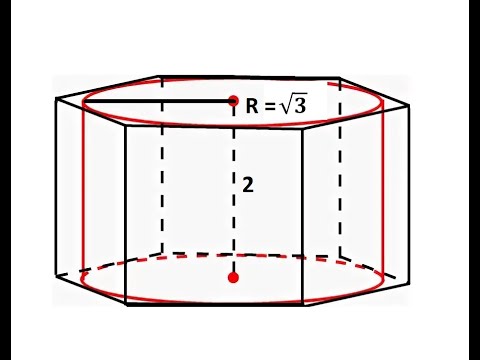
ЕГЭ 2022 математика задача 4 вариант 2
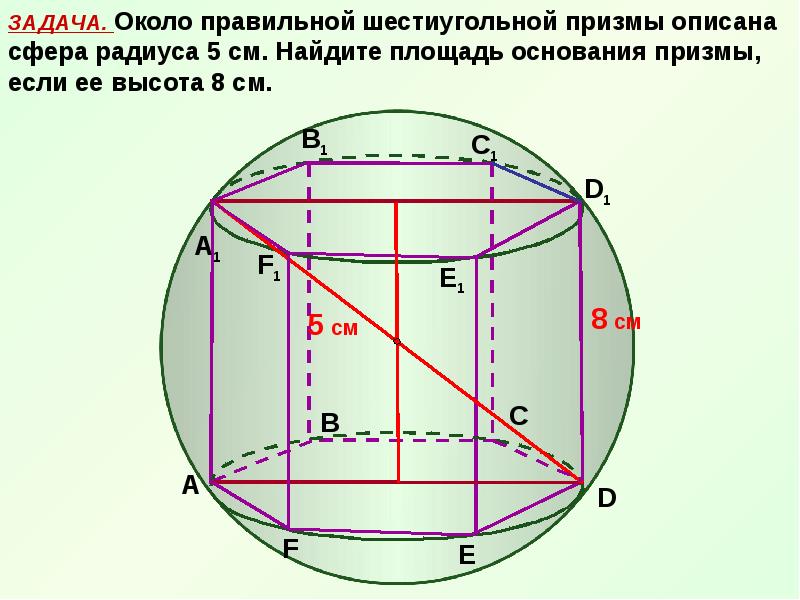
При расчете радиуса важно учесть, что призма с более сложными основаниями потребует дополнительных шагов для точного вычисления радиуса описанной сферы.
Геометрия, 11 класс. Вписанные и описанные шары и сферы