Особенности вычисления и применения противолежащих углов в равнобедренной трапеции
На этой странице представлены основные принципы и полезные советы по вычислению противолежащих углов в равнобедренной трапеции. Знание этих правил поможет вам лучше понять геометрические свойства этой фигуры и правильно применять их в решении задач.
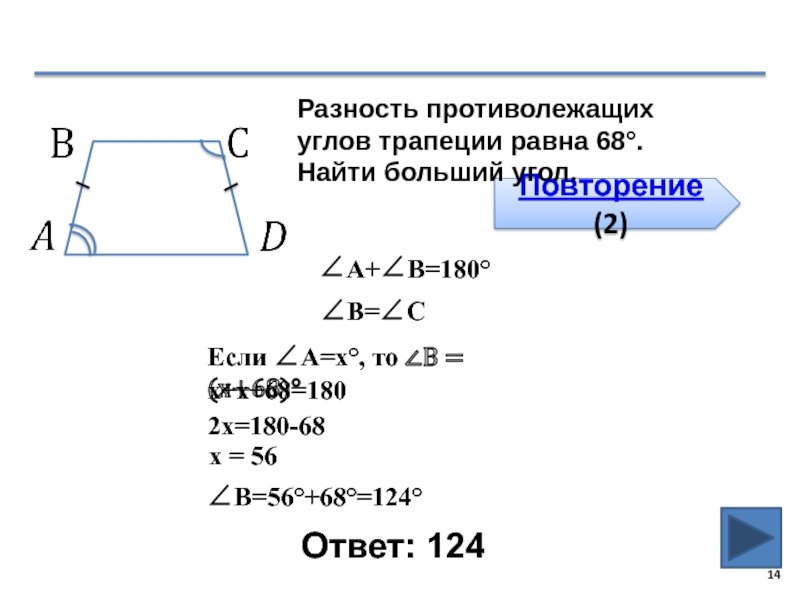
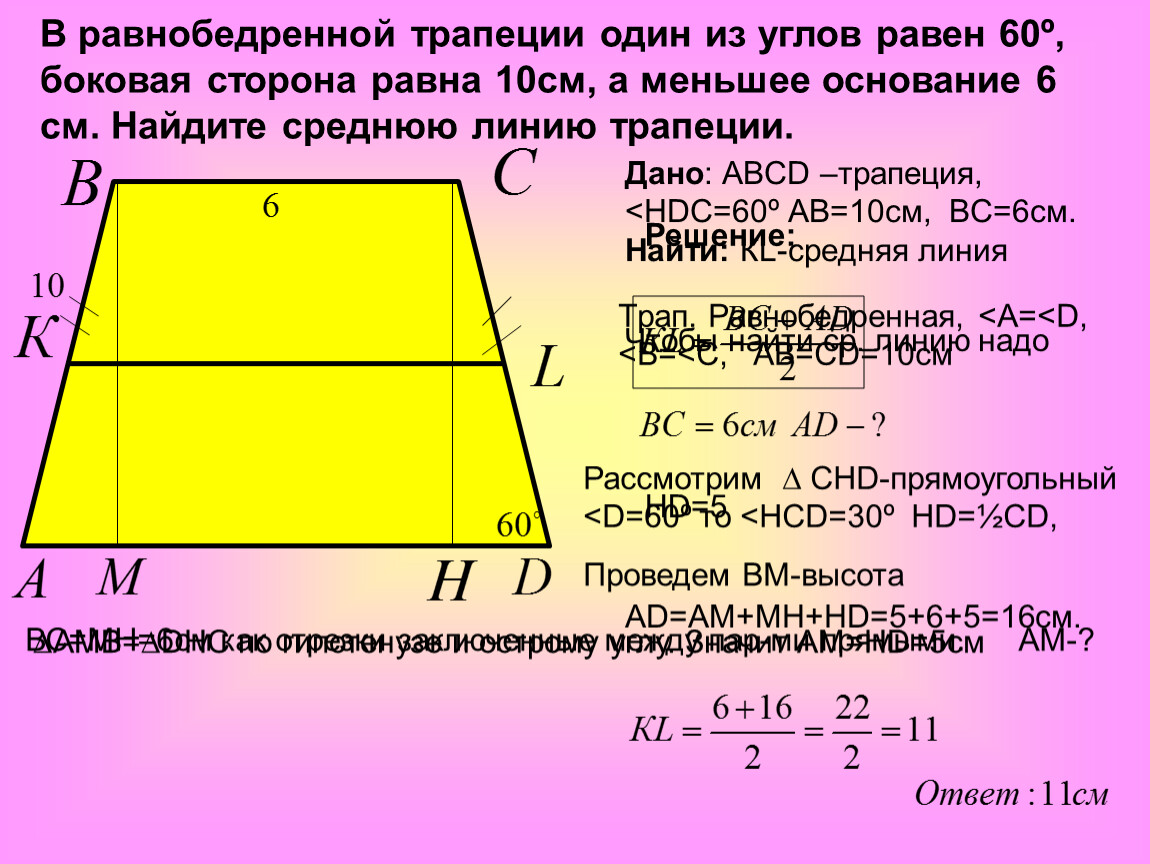
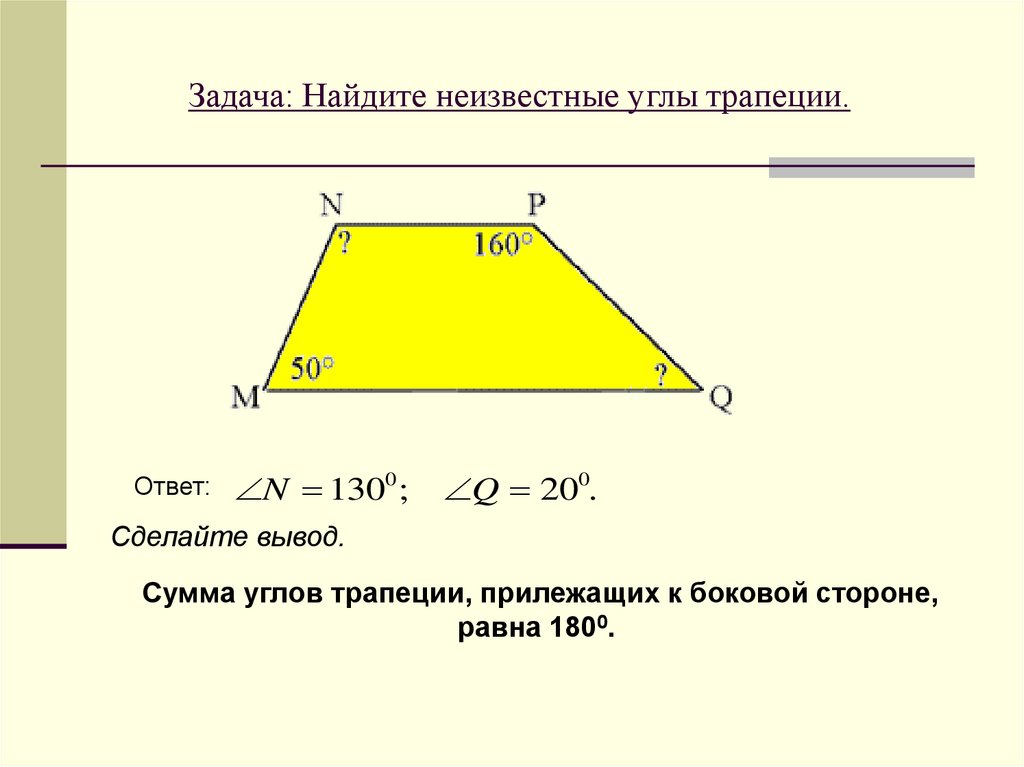
Чтобы вычислить противолежащие углы в равнобедренной трапеции, используйте свойство, что они всегда равны между собой.

Разность противолежащих углов равнобедренной трапеции известна. Найти больший угол
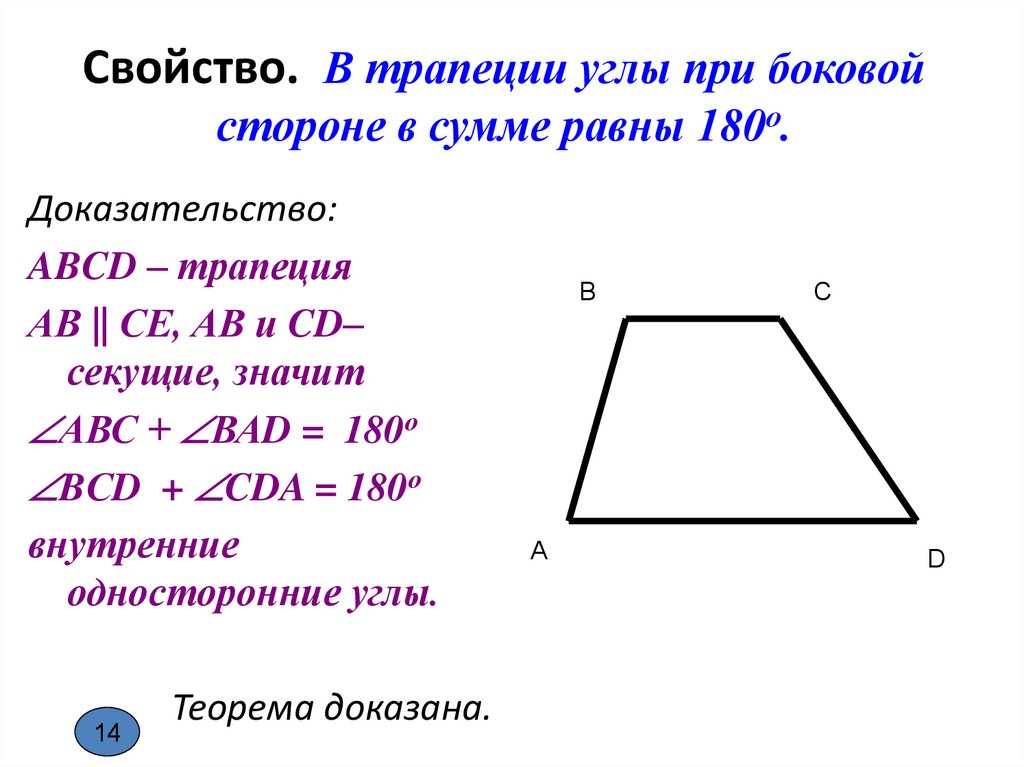
Противолежащие углы равнобедренной трапеции образуют пару углов, которые могут быть вычислены с помощью базовых тригонометрических функций.
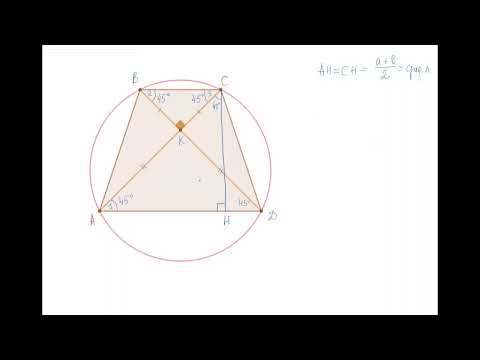
Малоизвестные свойства равнобедренной трапеции. Разбор задачи 17 ЕГЭ профиль.
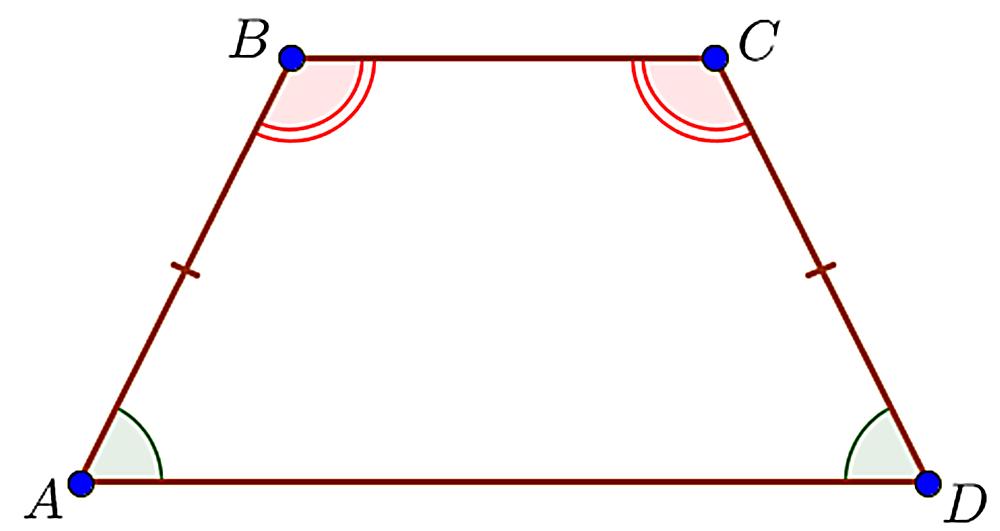
Для упрощения вычислений можно воспользоваться известной теоремой о внешнем угле, который равен сумме двух внутренних.

чему равен больший угол равнобедренной трапеции если разность противолежащих углов равна 6
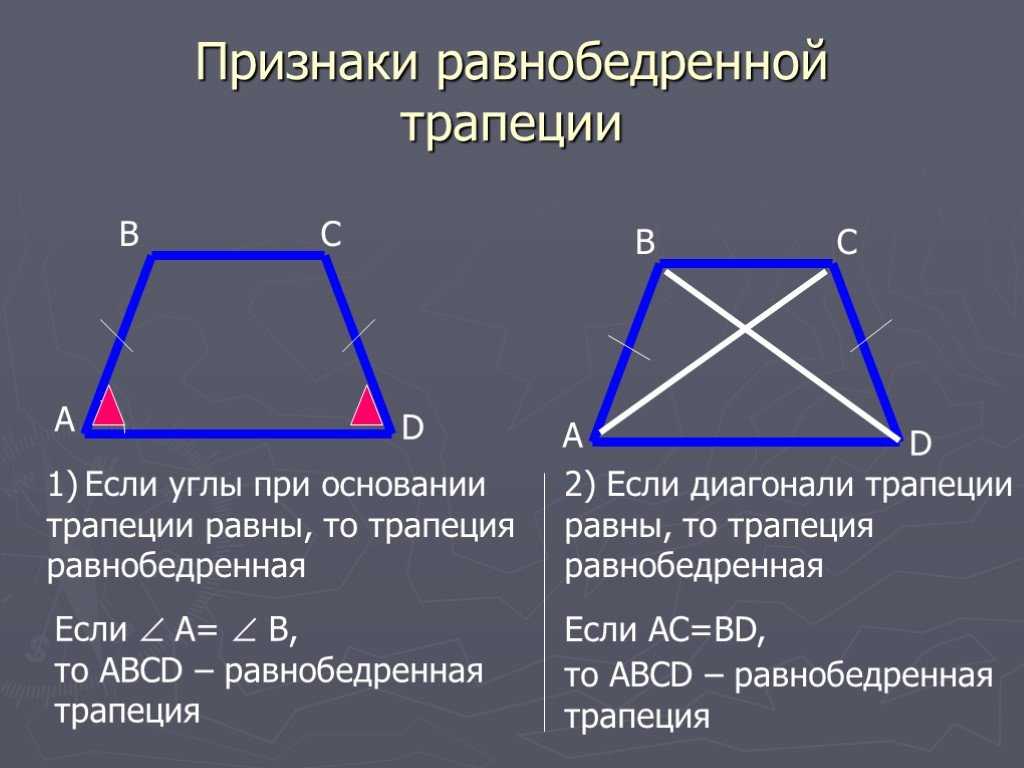

При решении задач на равнобедренные трапеции помните, что угол между боковыми сторонами всегда одинаков в каждой из трапеций.

Трапеция. Задачи. Найти углы трапеции. Равнобедренной,прямоугольной,
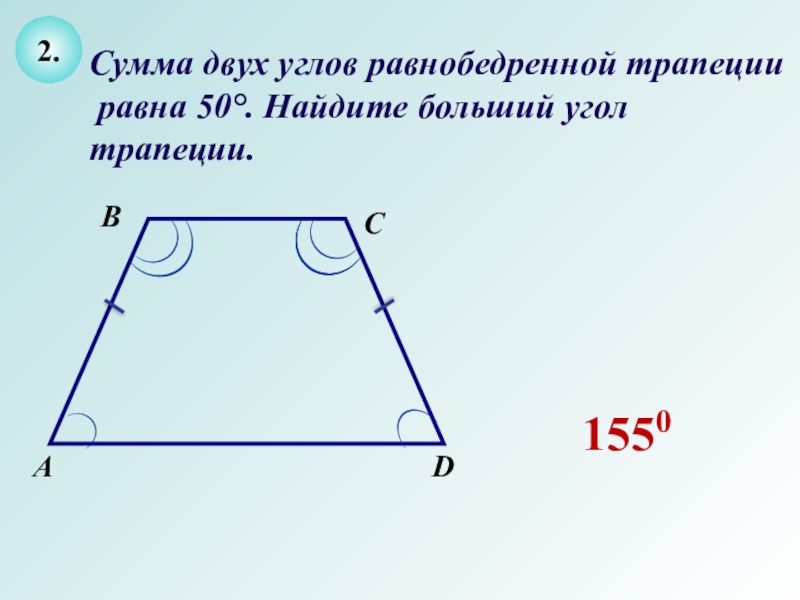
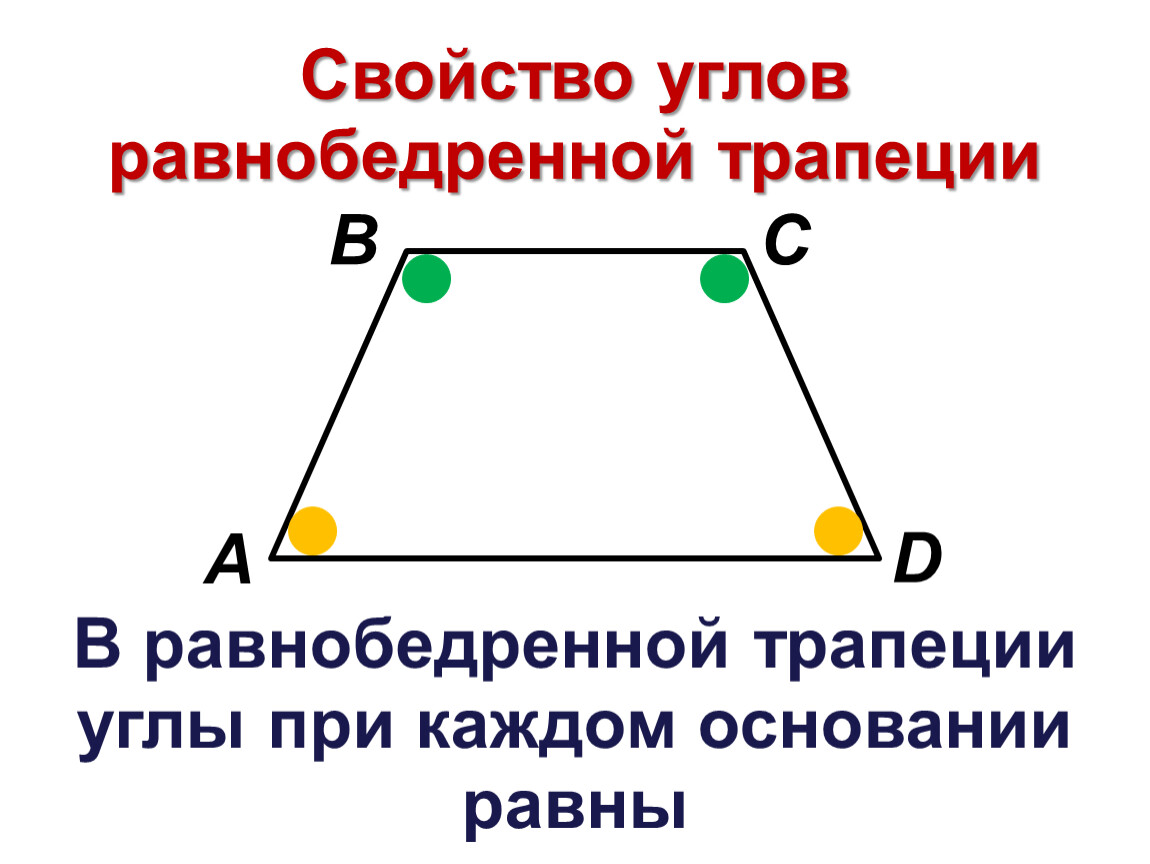
Визуально определите углы, учитывая симметрию фигуры: углы при основаниях всегда равны.
РАВНОБЕДРЕННАЯ ТРАПЕЦИЯ 😉 #егэ #математика #профильныйегэ #shorts #огэ
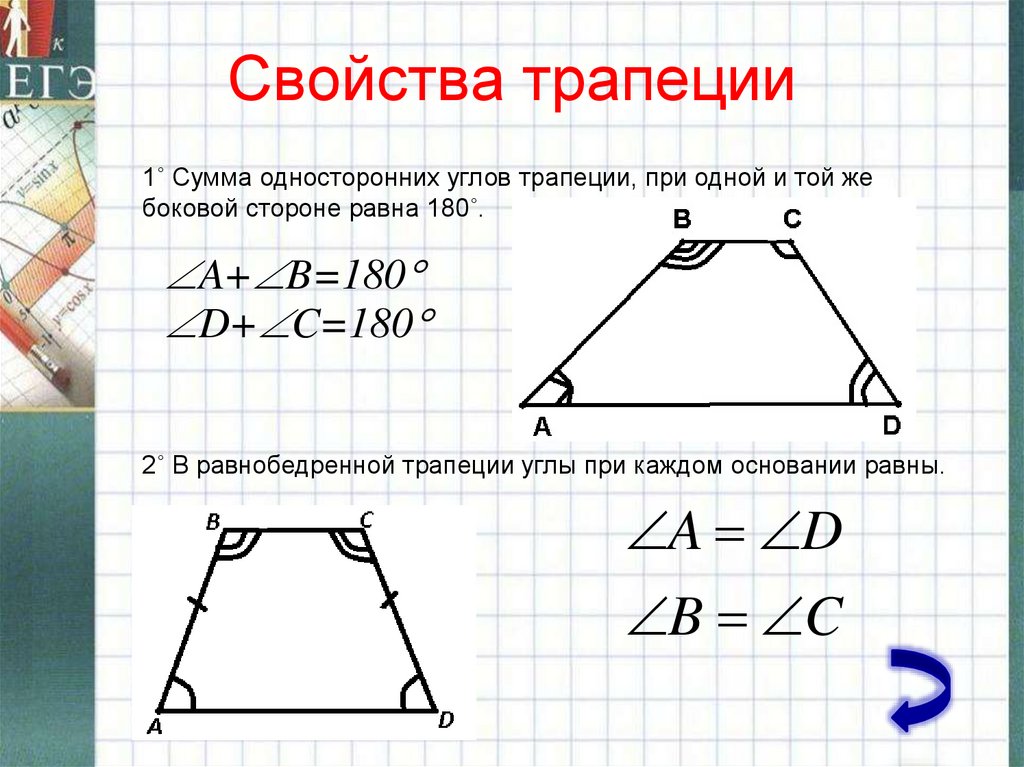

Используйте правило, что сумма углов трапеции всегда равна 360 градусам, чтобы проверять правильность расчетов.
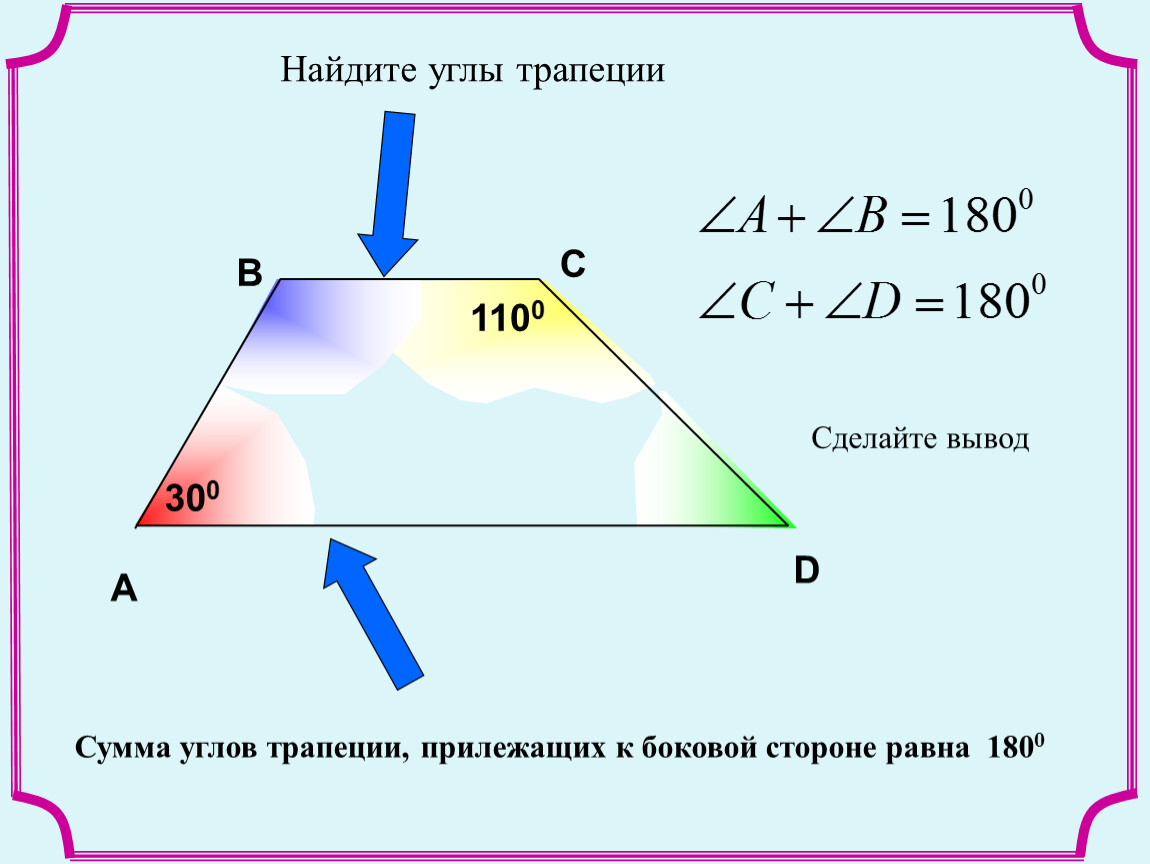
Чтобы найти углы в равнобедренной трапеции, достаточно знать только один угол у основания, так как остальные углы можно вычислить с помощью его значения.
В практике важно учитывать, что противолежащие углы равнобедренной трапеции всегда могут быть использованы для вычисления других геометрических параметров.

Как найти углы трапеции - Свойства трапеции - Как решить задачу из пособия Балаян. 8кл+
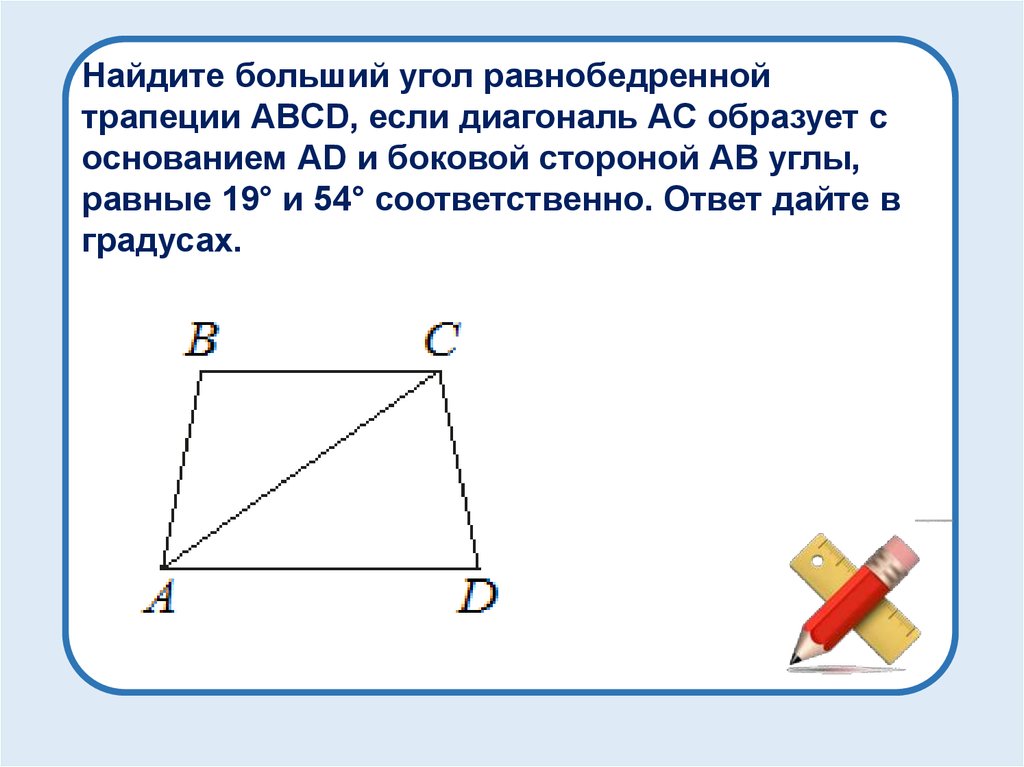
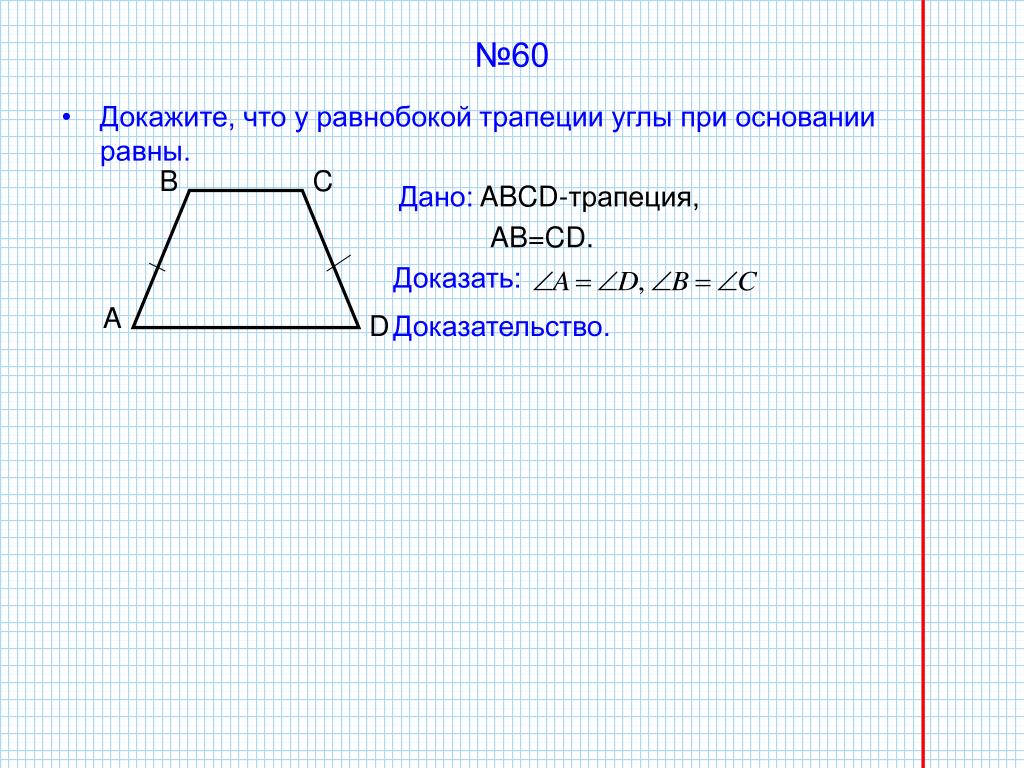
Если трапеция задана через длины сторон, используйте теорему синусов для более точного вычисления углов.

№388. Докажите, что в равнобедренной трапеции: а) углы при каждом основании равны
Не забывайте, что равенство противолежащих углов является важным инструментом для построения геометрических фигур, связанных с трапециями.
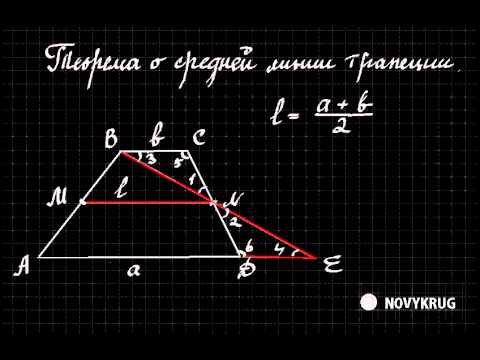
Теорема о средней линии трапеции