Пошаговый процесс нахождения производной функции двух переменных в конкретной точке
На данной странице вы найдете подробное руководство по вычислению производной функции двух переменных в точке. Разберем основные шаги, используемые методы и примеры для лучшего понимания темы.



Начните с вычисления частных производных по каждой из переменных.

Математический анализ, 29 урок, Функции нескольких переменных. Частные производные

Обязательно учитывайте, что для нахождения производной функции двух переменных требуется знать значения частных производных в точке.

Математика без Ху%!ни. Экстремум функции 2х переменных.
Используйте градиент функции для анализа изменений в разных направлениях.

2. Область определения функции двух переменных


Если функция задана в виде формулы, вычислите частные производные аналитически.

6. Частные производные функции двух переменных

Для проверки результатов можно использовать численные методы приближенного вычисления производных.

Математика без Ху%!ни. Частные производные функции нескольких переменных. Градиент.


Будьте внимательны к условиям существования производных в точке, особенно если функция имеет разрывы или особенности.

Запомните, что производная функции в точке может иметь физический или геометрический смысл в зависимости от контекста задачи.

Использование математического ПО, например, Wolfram Alpha или MATLAB, может существенно упростить вычисления.

Частные производные функции многих переменных
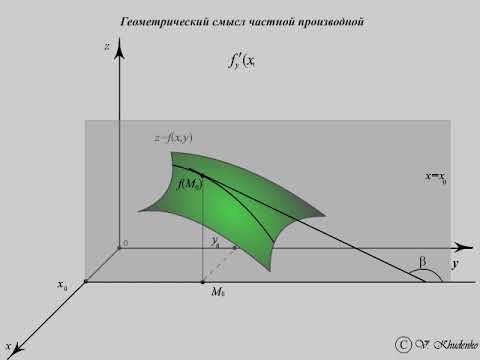
Геометрический смысл частной производной

Для более глубокого понимания темы полезно изучать теорему о дифференцируемости функций нескольких переменных.

Решение типичных задач на производную функции двух переменных помогает лучше освоить материал и ускоряет подготовку к экзаменам.


Вторая производная, Точки перегиба - Производная - Математический анализ