Проекция треугольника на плоскость: советы для точных вычислений и визуализаций
Проецирование треугольника на плоскость — это важная техника в геометрии и математике, которая применяется для упрощения сложных пространственных задач. В этой статье мы расскажем о ключевых аспектах проекции треугольника, различных методах и дадим полезные рекомендации для точных вычислений и визуализаций.
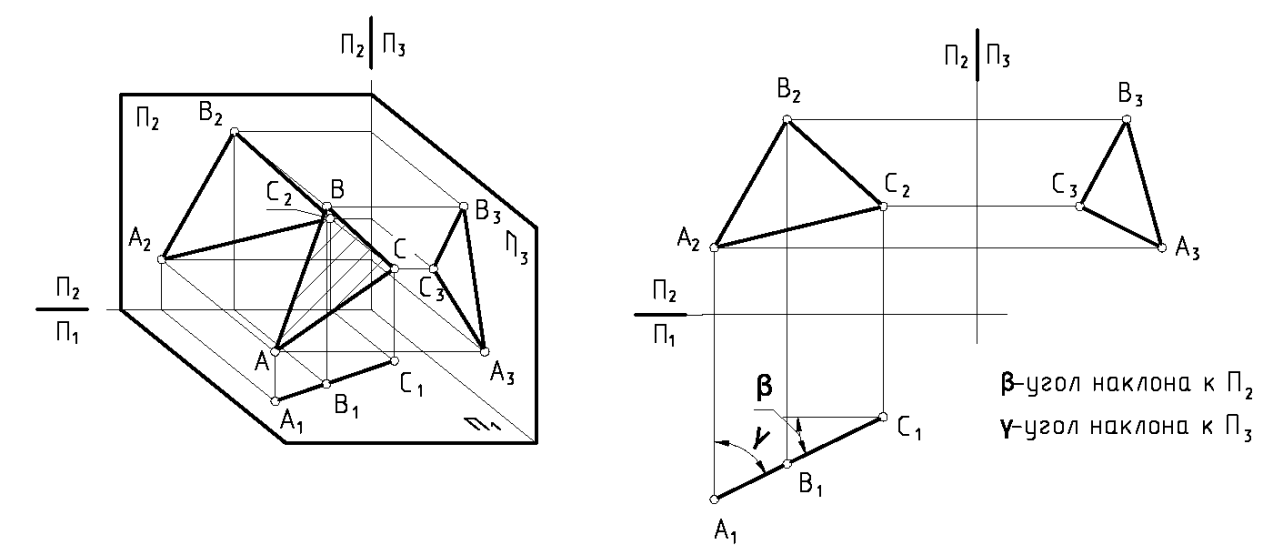
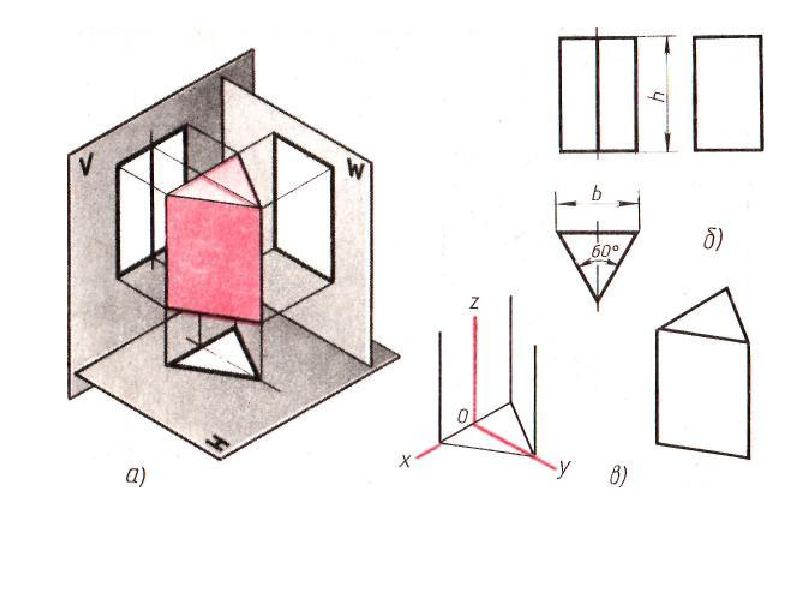
Перед началом проекции убедитесь, что вы правильно понимаете расположение треугольника в пространстве и его ориентацию относительно плоскости.

Способ замены (перемены) плоскостей проекции. Определение истинной величины отрезка и плоской фигуры
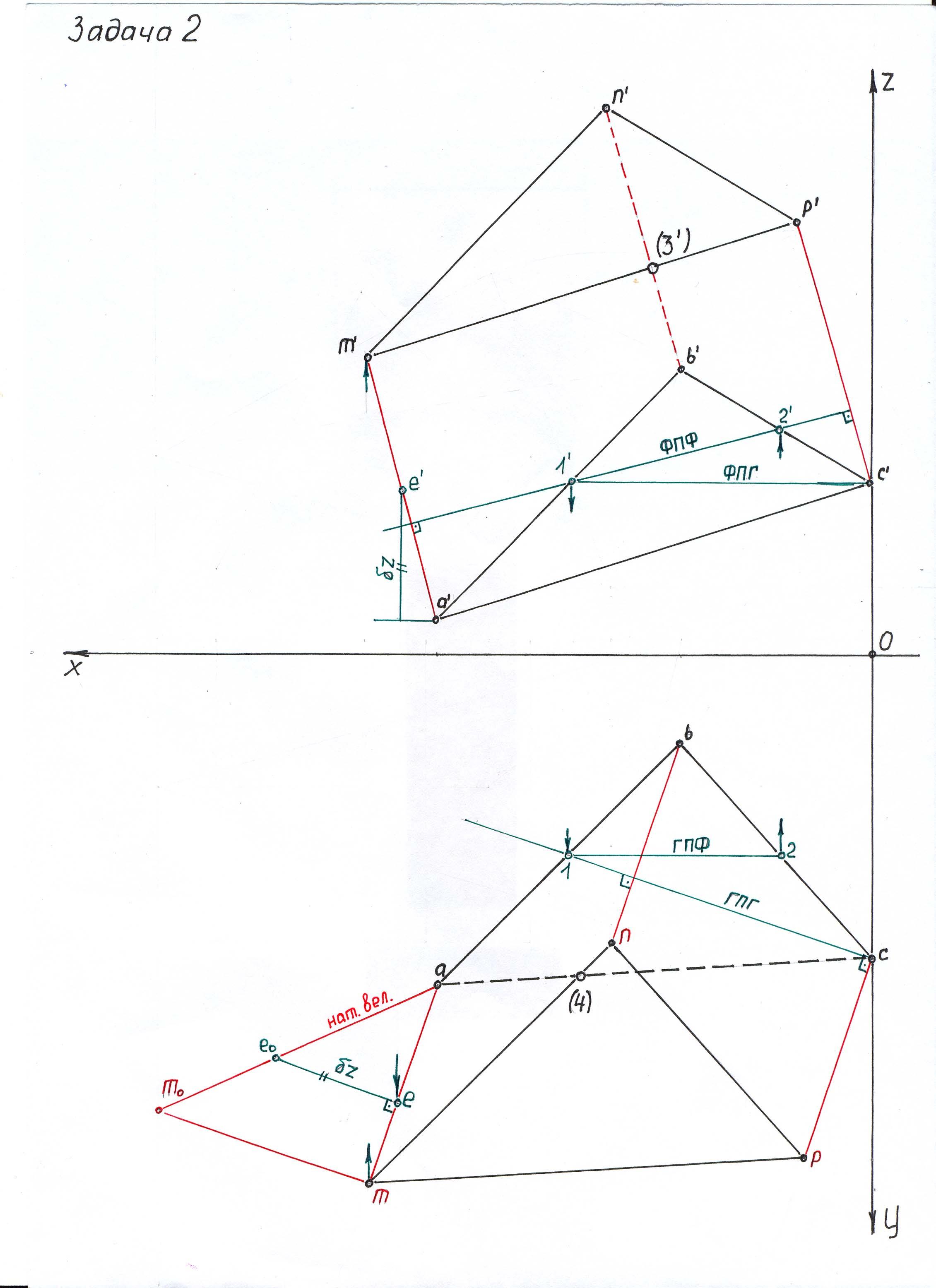
Используйте стандартные геометрические преобразования, такие как вращение и перенос, чтобы упростить задачу проекции треугольника.

Построение параллельной плоскости на расстояние 30 мм.


При проекции треугольника важно учитывать перспективу, поскольку она может значительно влиять на внешний вид и точность изображения.

Построение недостающей проекции плоскости. Принадлежность прямой к плоскости
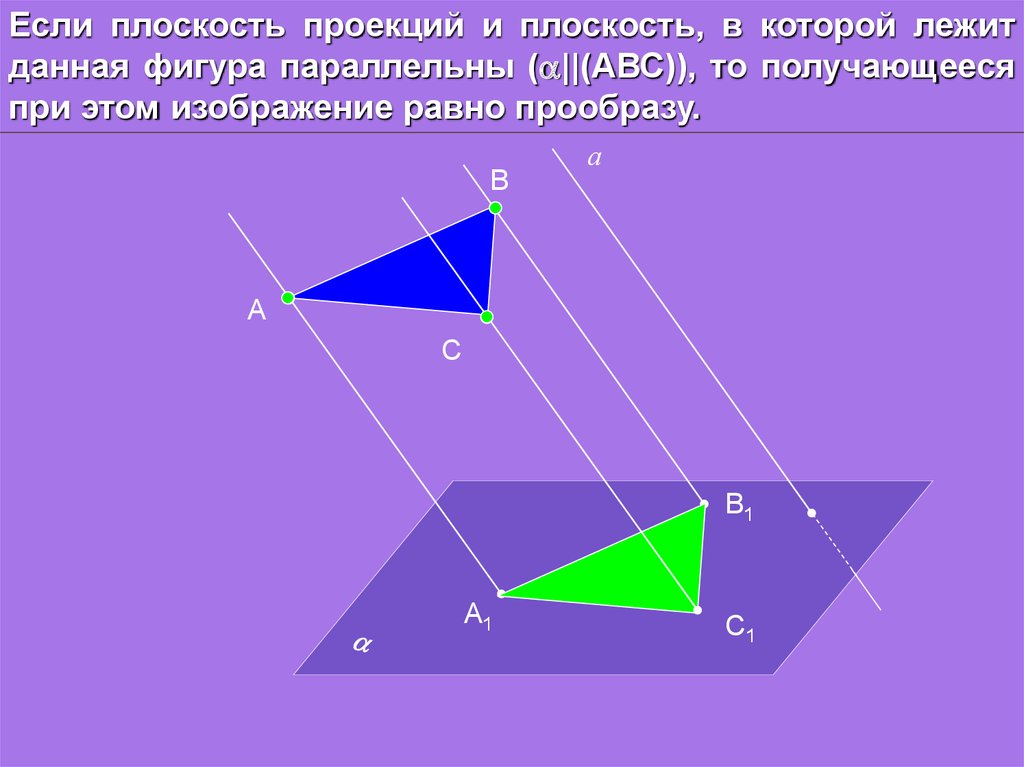
Для лучшего понимания проекции используйте графические программы или математические инструменты, которые помогут визуализировать процесс.

Решаем ОГЭ по физике 2025 - Полный разбор 11 варианта из сборника Камзеевой - Физика ОГЭ
При проекции убедитесь, что все углы и стороны треугольника соблюдают правильные пропорции относительно плоскости.
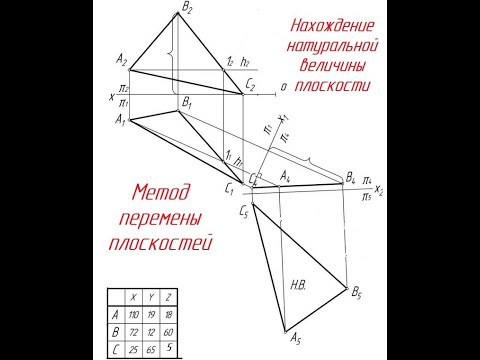
СПОСОБ ПЕРЕМЕНЫ ПЛОСКОСТЕЙ
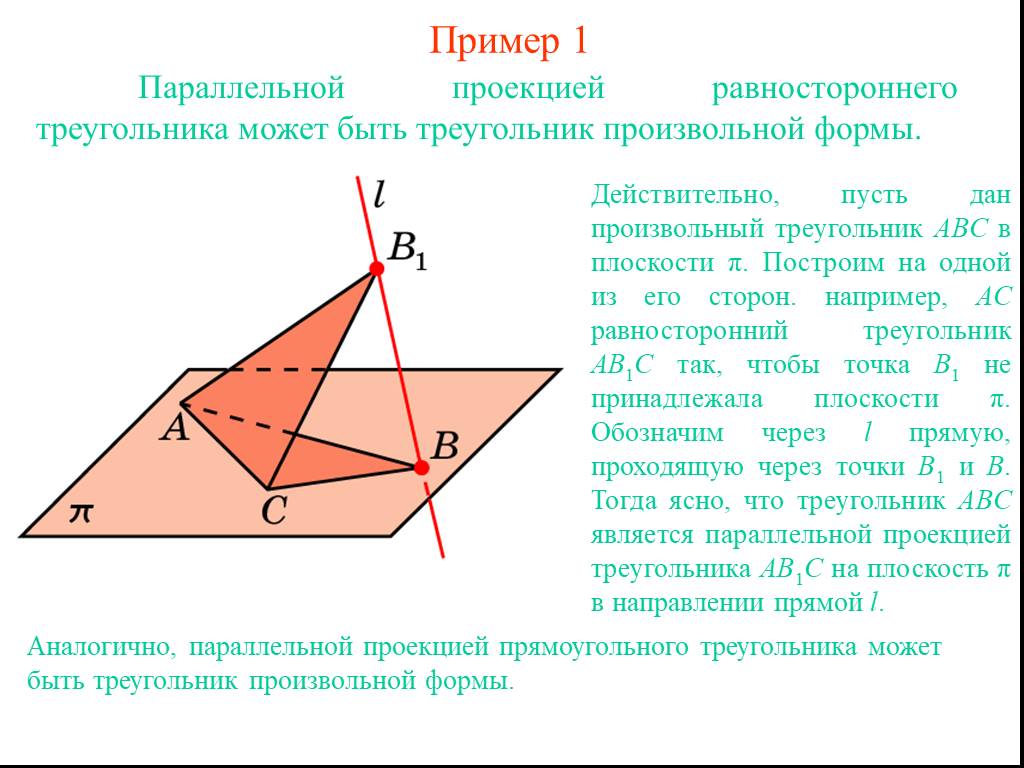
Внимательно следите за точностью измерений при проекции, поскольку даже небольшая погрешность может исказить результат.

Если проекция треугольника осуществляется на наклонную плоскость, необходимо учитывать угол наклона плоскости относительно оси проекции.
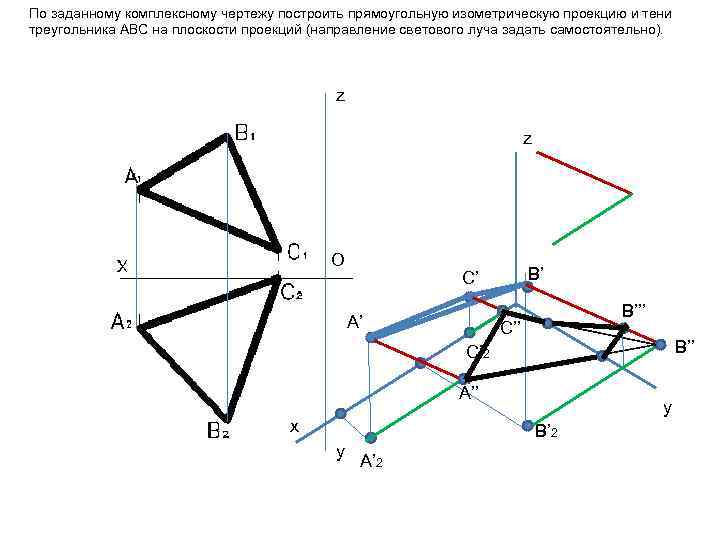
При работе с проекциями треугольников в разных плоскостях полезно использовать метод ортогональных проекций для упрощения вычислений.

Перед выполнением проекции на плоскость, определите координаты вершин треугольника и выберите соответствующую систему координат для проекции.
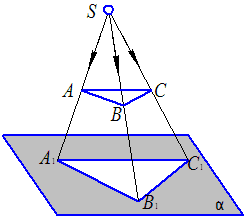
Для сложных задач используйте симметричные методы проекции, чтобы уменьшить количество вычислений и повысить точность результатов.

Определение натуральной величины треугольника АВС методом замены плоскостей проекции