Основные методы нахождения проекции одного отрезка на другой с примерами и объяснениями
Проекция отрезка на отрезок — это важная геометрическая операция, которая находит применение в различных областях математики и физики. Важно понимать, как правильно вычислить проекцию и использовать её для решения задач. В этом разделе мы подробно расскажем о том, как это сделать и приведем полезные советы для практического применения данной концепции.
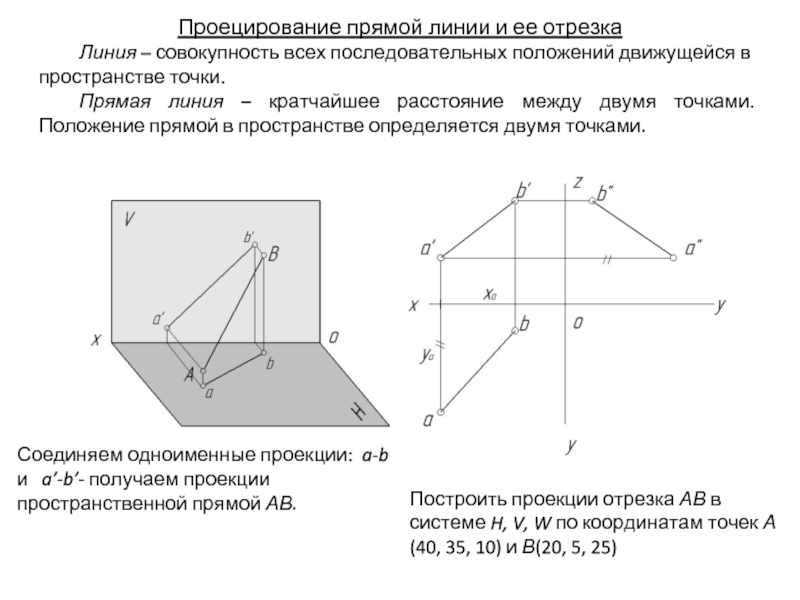
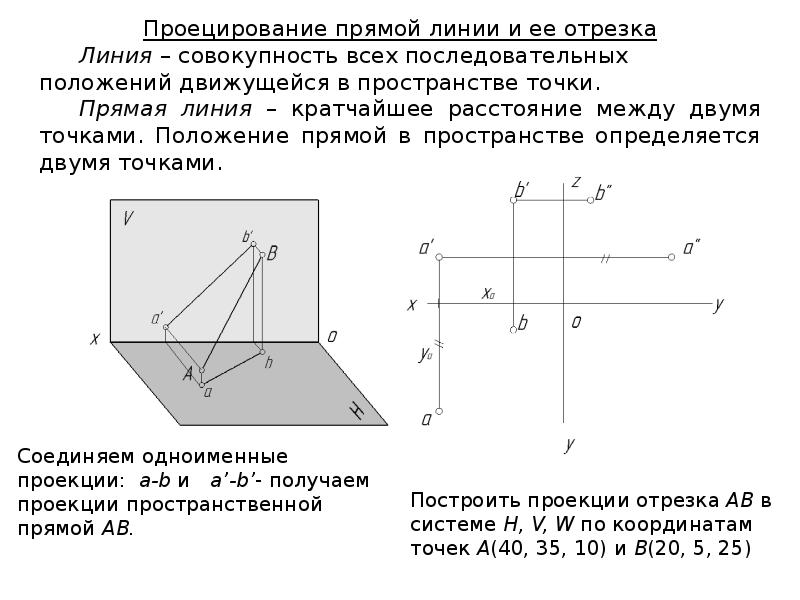
Для начала определите, на какой отрезок будет происходить проекция, а затем используйте перпендикуляр для нахождения точки проекции.
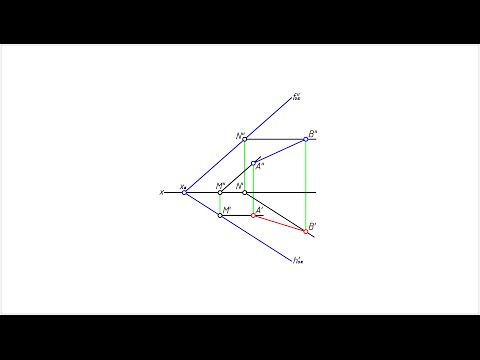
Построение недостающей проекции отрезка прямой линии, лежащей в заданной плоскости
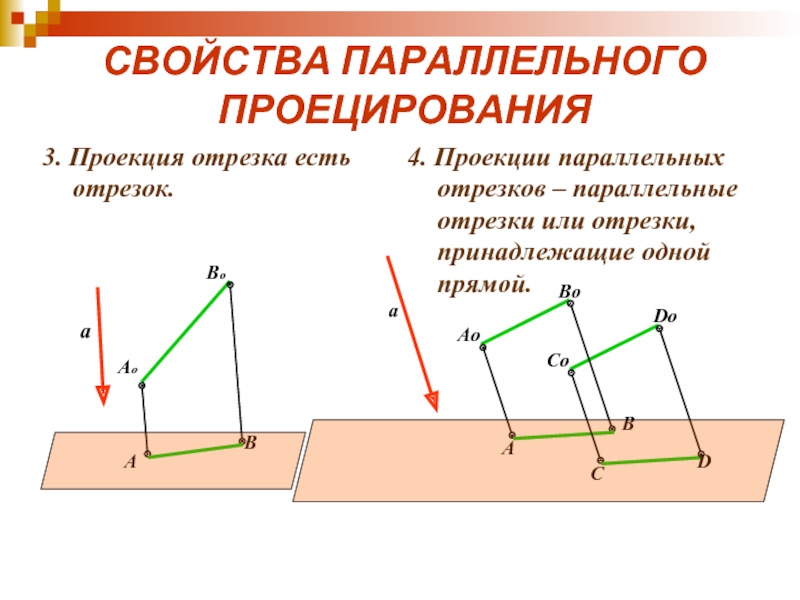
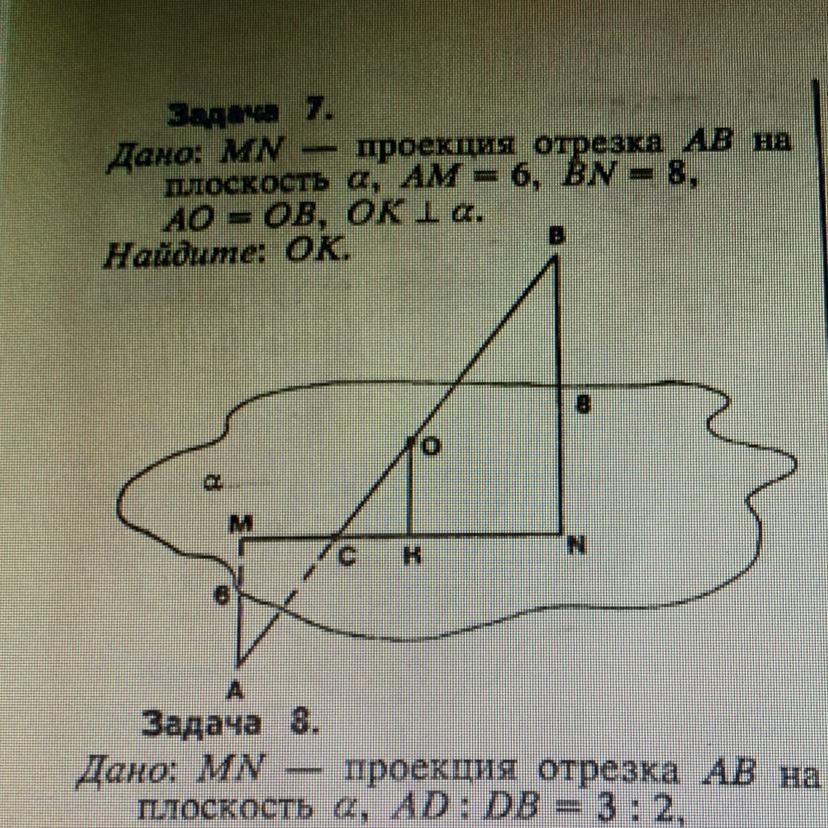
Чтобы избежать ошибок при вычислениях, всегда проверяйте, лежит ли точка проекции на самом отрезке.

Построить проекции линии и точек на ней по заданным координатам. Начертательная геометрия
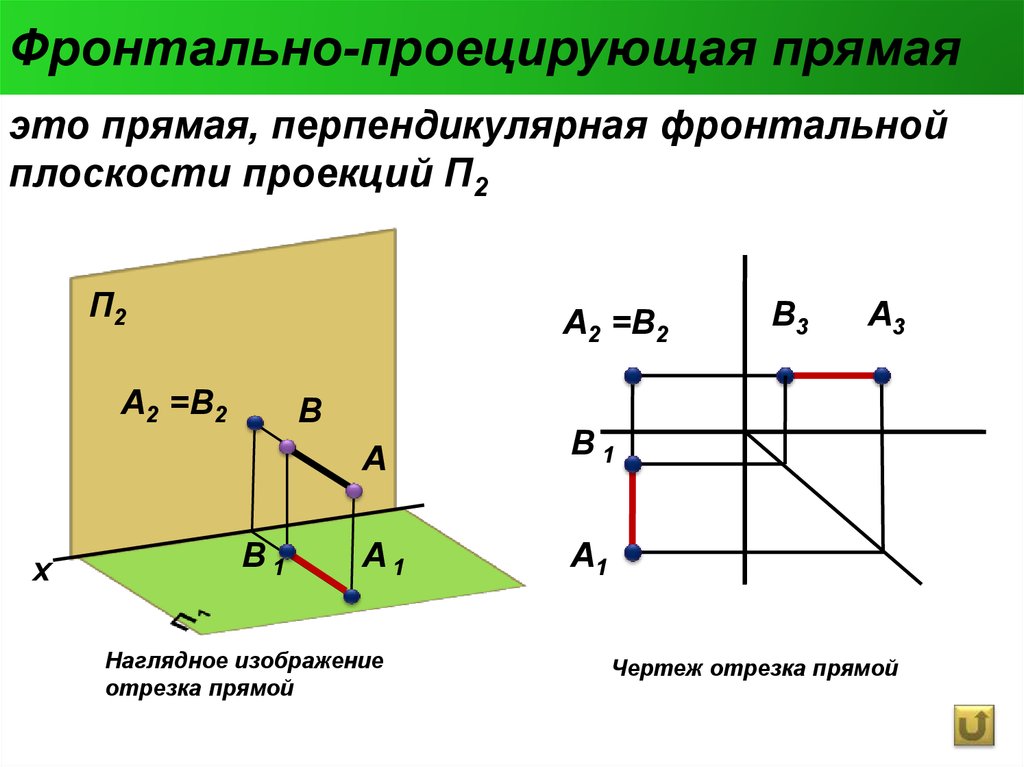
При выполнении проекции важно учитывать ориентацию отрезков, чтобы корректно вычислить результат.

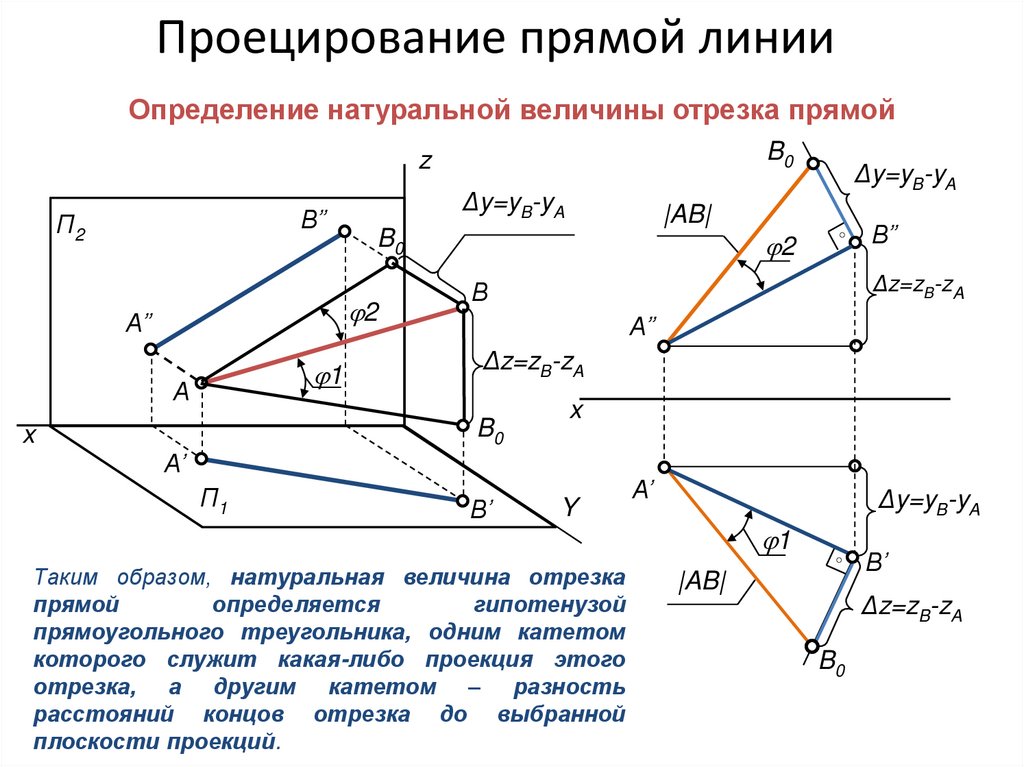
Проецирование прямой общего положения
Если отрезки пересекаются, проекция может быть точкой на пересечении, а не отрезком.
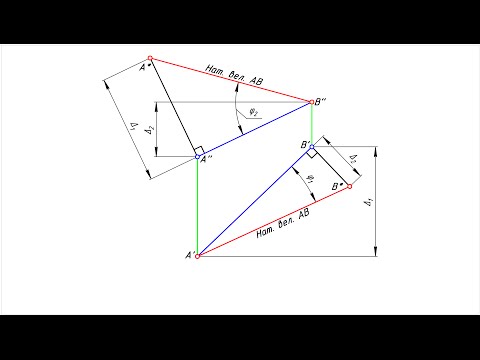
Натуральная величина отрезка
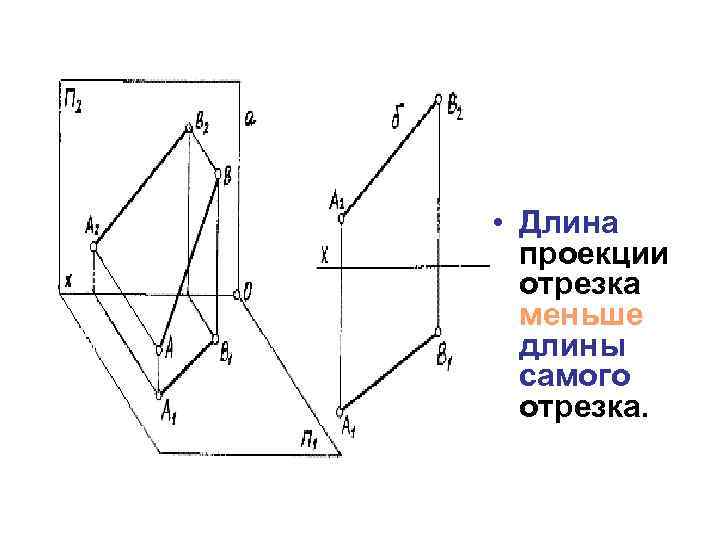
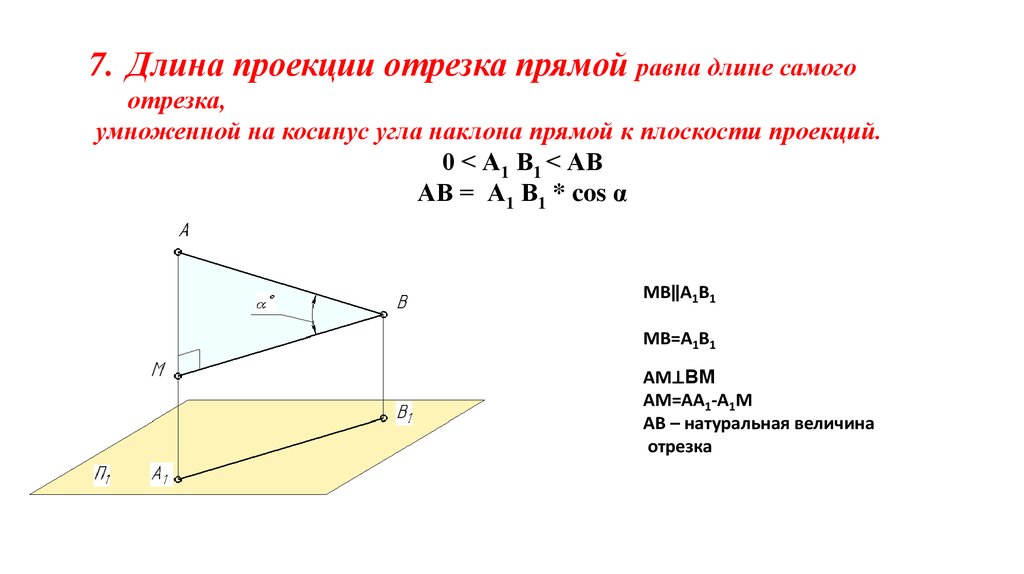
Использование координатной геометрии может значительно упростить процесс нахождения проекции, особенно если отрезки заданы в координатах.

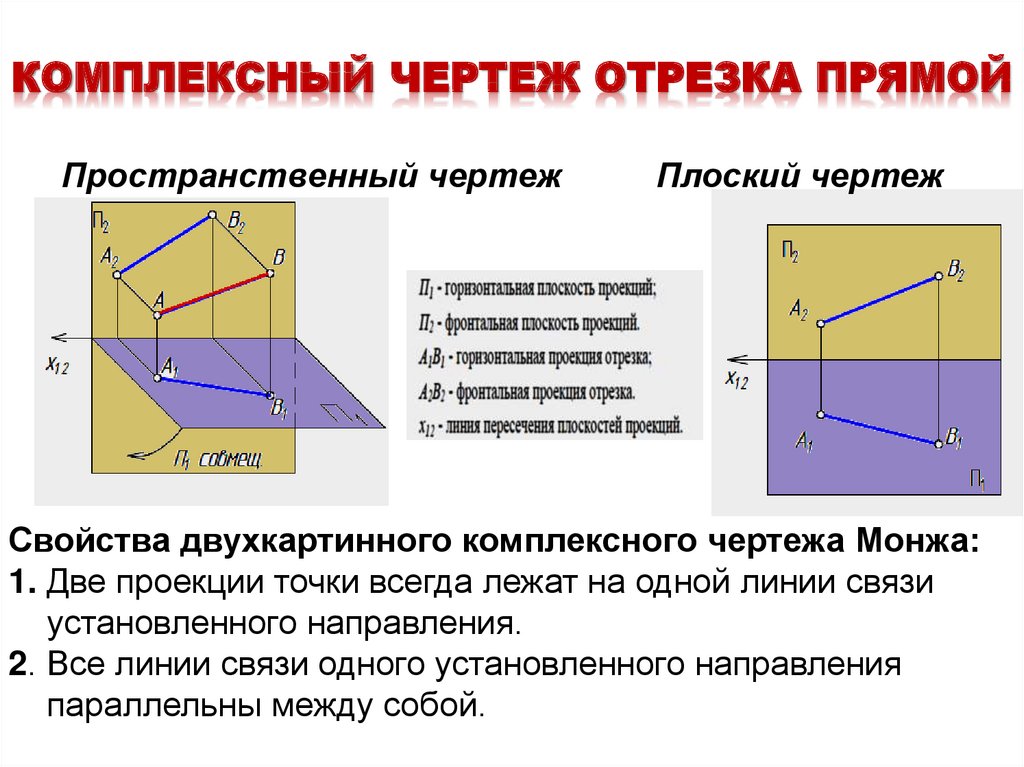
2. Построение недостающей фронтальной проекции отрезка прямой

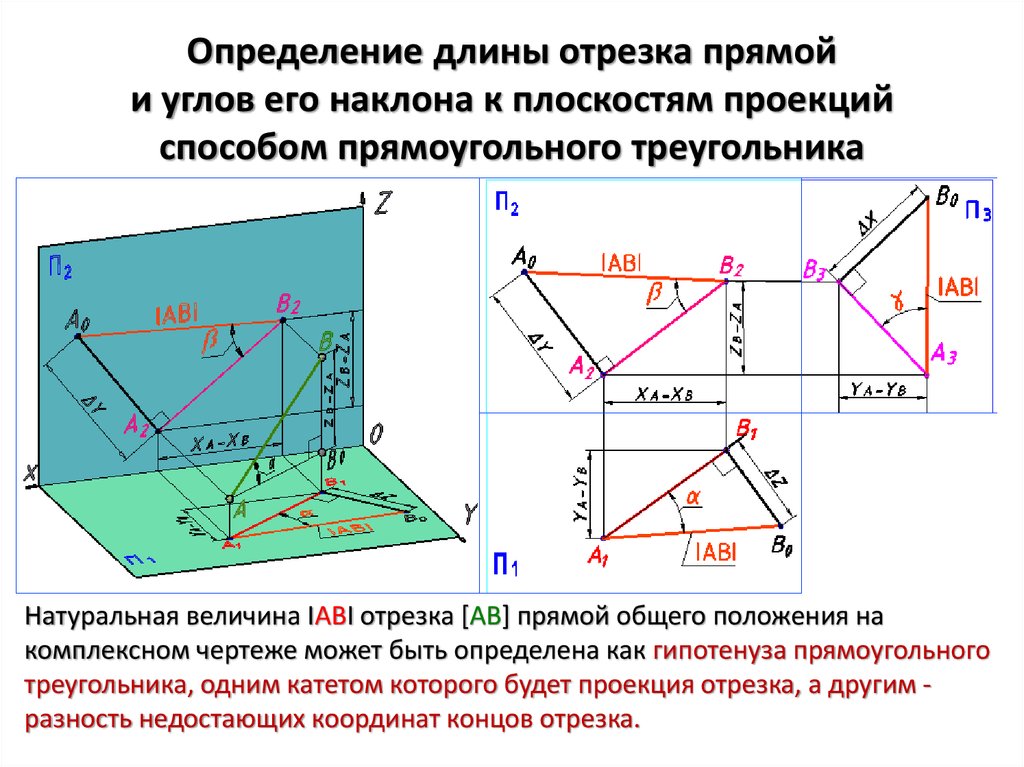
Для более сложных случаев можно использовать формулы векторной алгебры для вычисления проекции отрезка на отрезок.
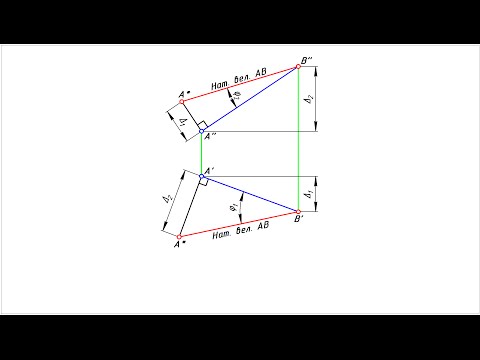
Натуральная величина отрезка
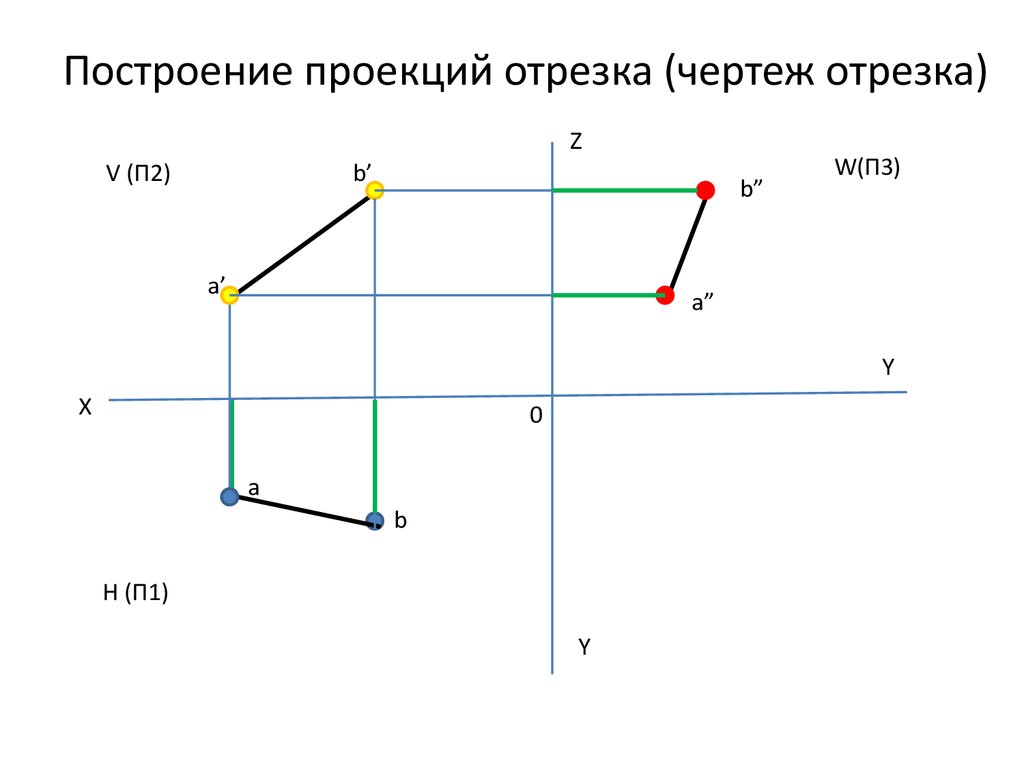
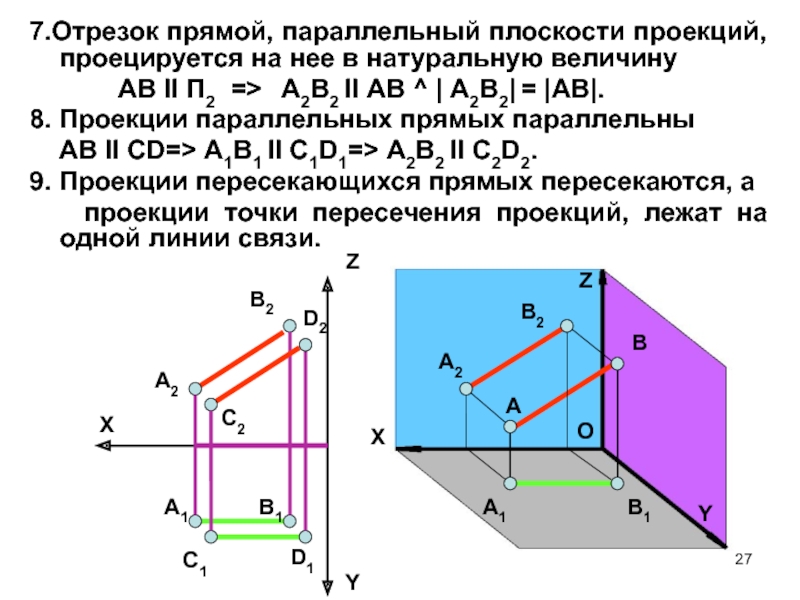
Помните, что проекция не всегда будет целым отрезком, иногда результатом будет одна точка.
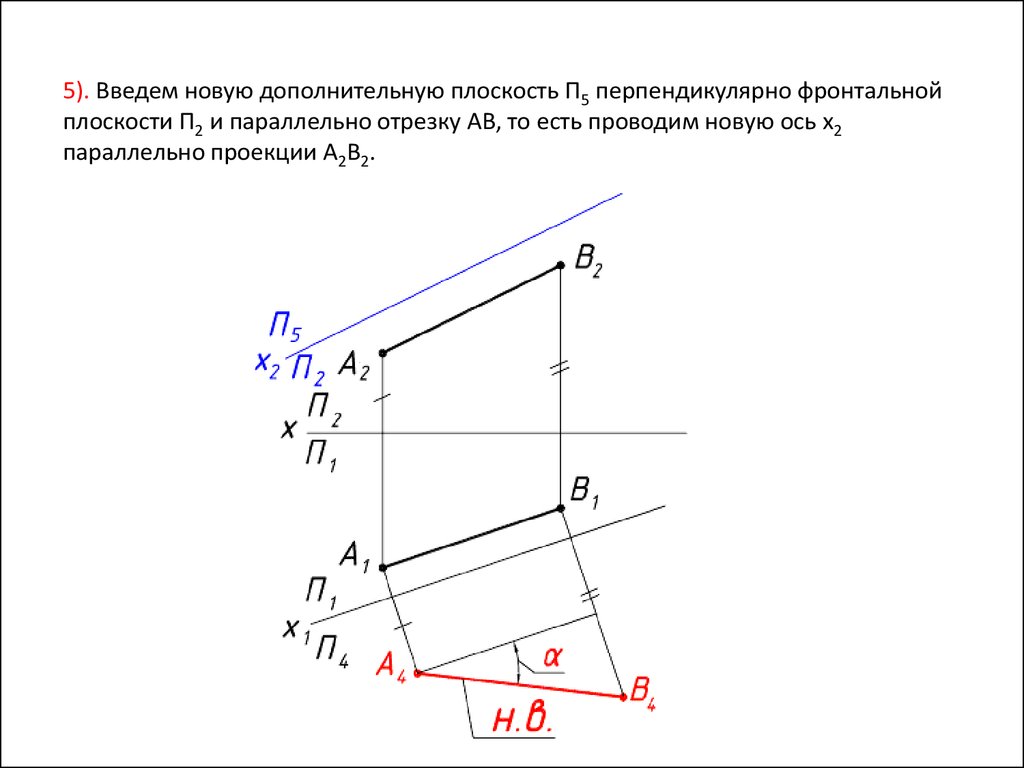
Используйте графическое представление для визуализации проекции, чтобы лучше понять процесс и избежать ошибок в расчетах.
Проекции точки,отрезка,плоскости в ортогональном likerkacinema.ruие(likerkacinema.ruИОННОЕЧЕРЧЕНИЕ)

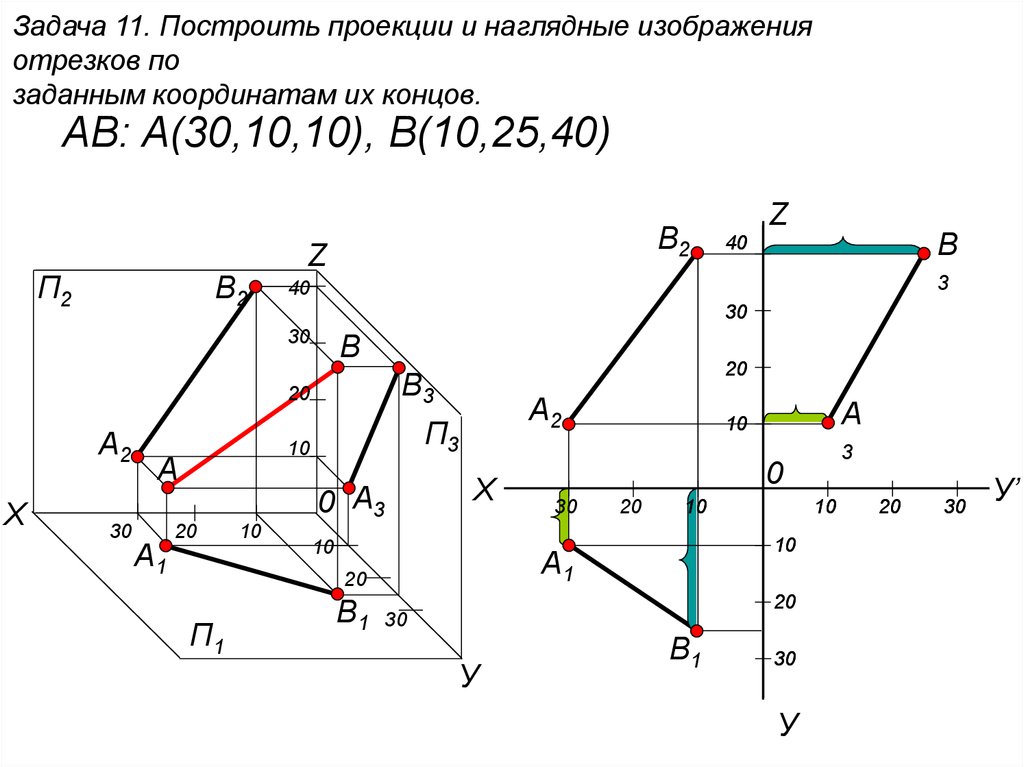
Не забывайте, что проекция отрезка на отрезок всегда является множеством точек, которое может быть пустым, если отрезки не пересекаются.

Если задача состоит в нахождении расстояния между отрезками, то проекция одного из отрезков на другой поможет вам найти минимальное расстояние между ними.

Способ замены (перемены) плоскостей проекции. Определение истинной величины отрезка и плоской фигуры