Представление числа как произведения двух чисел: пошаговое руководство и советы
Представление числа в виде произведения двух чисел — это полезный математический прием, который помогает понять его структуру и свойства. Это особенно важно при разложении чисел на множители, поиске простых чисел или решении задач на делимость. В этой статье мы рассмотрим различные способы представления чисел и предоставим практические советы, которые помогут вам освоить этот метод.


При разложении числа на множители всегда начинайте с поиска простых делителей, таких как 2, 3, 5, 7 и так далее.

Увеличь кровоснабжение мозга. Зрение четче, слух острее, ясная голова, хорошая память.


Использование таблицы умножения поможет быстро и эффективно находить множители для меньших чисел.

Процентное отношение двух чисел. 6 класс


Если число четное, первым делителем всегда будет 2, что значительно ускоряет процесс разложения.
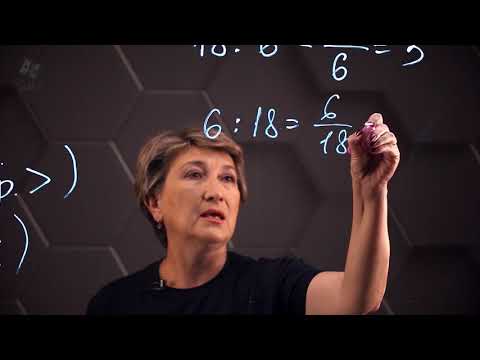
Отношение двух чисел. 6 класс.


Разбирая большие числа, используйте метод деления на простые числа, чтобы получить более точное разложение.

Эффектный метод произведения двух чисел


Для чисел, не имеющих простых делителей, попробуйте их разложить на множители с использованием различных техник, таких как метод проб и ошибок.

Разложение составных чисел на простые множители. 5 класс.

При работе с большими числами полезно применять факторизацию с использованием калькулятора или специализированных программ для быстрого нахождения множителей.
Важно помнить, что каждый номер можно разложить на произведение множителей только один раз, используя простые числа.

Возведение в степень произведения и степени. Алгебра, 7 класс


Для чисел, имеющих несколько множителей, всегда ищите комбинации, которые дают наименьшее количество множителей, чтобы упростить вычисления.
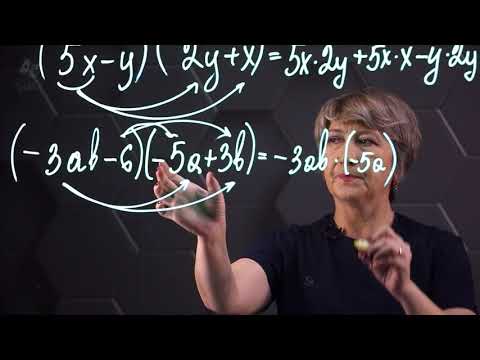
Произведение многочленов. 7 класс.
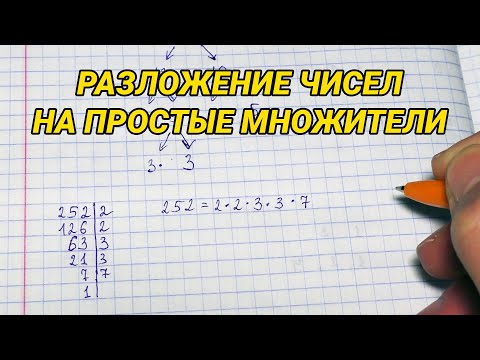
Разложение чисел на простые множители. Как разложить число на множители

При разложении чисел на множители всегда проверяйте, является ли результат произведением простых чисел.

ПРОГНОЗ И РЕКОМЕНДАЦИИ НА 2025 — Гуру Фэншуй / НАТАЛЬЯ ПРАВДИНА

Не забывайте, что любое число больше 1 можно представить в виде произведения множителей, даже если это не очевидно на первый взгляд.

Как представить многочлен в виде произведения. Алгебра 7 класс

