Правила формирования числовых рядов: секреты, которые помогут решить любые математические задачи

На этой странице вы найдете полезные советы по тому, как правильно разбирать и составлять ряды чисел, а также научитесь выявлять закономерности, которые помогут вам решать задачи с числовыми последовательностями. Важные правила и методы подойдут как для новичков, так и для опытных математиков.

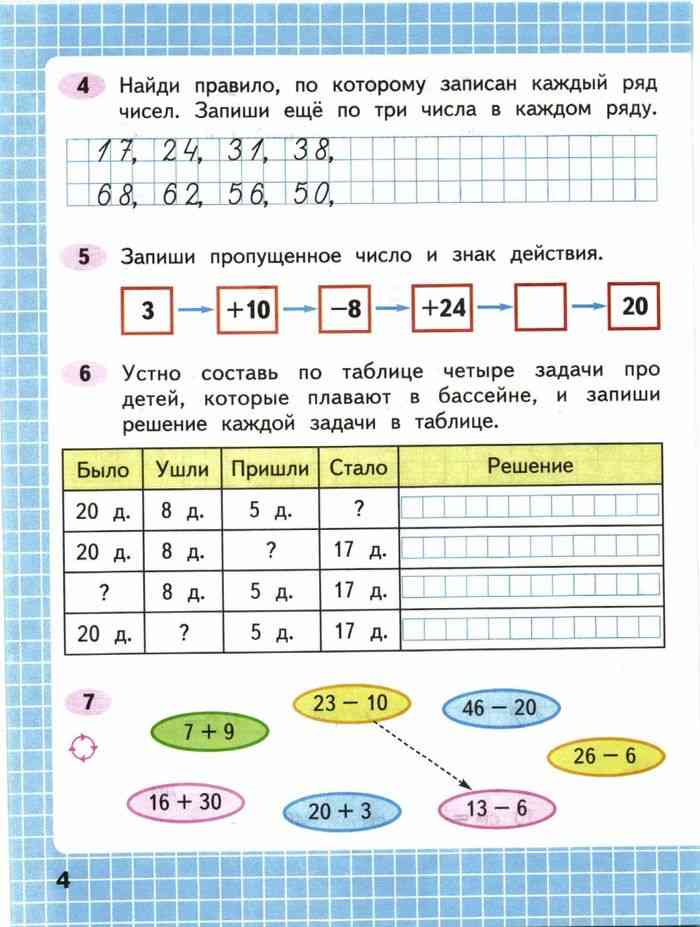
При работе с числовыми рядами всегда обращайте внимание на возможные арифметические или геометрические прогрессии, они могут быть основой многих рядов.

Если последовательность не очевидна, попробуйте анализировать разницу или частное между соседними числами для поиска закономерностей.

Для более сложных задач используйте метод подбора и проверки, проверяя разные гипотезы на конкретных примерах.

Наблюдайте за тем, как изменяется разница между числами: иногда это может помочь понять, является ли ряд арифметической прогрессией или его элементы связаны другими операциями.

Пробуйте рассматривать ряд как комбинацию нескольких простых последовательностей, иногда это поможет увидеть скрытые связи.

Используйте алгоритмическое мышление: если ряд имеет нестандартное правило, попробуйте построить формулу или алгоритм для его построения.

Если в ряду присутствуют дробные или десятичные числа, ищите закономерности в их дробных частях или преобразовывайте их в более простую форму.

Не забывайте проверять, можно ли представить ряд в виде полинома или других математических объектов, это может раскрыть структуру последовательности.

Если ряд заканчивается на какой-то особенный элемент, посмотрите, не является ли этот элемент исходным значением для следующего ряда или последовательности.

Практикуйтесь на простых числовых рядах: чем больше задач вы решите, тем быстрее начнете распознавать возможные закономерности в более сложных рядах.