Изучаем многогранники Пифагора: ключевые моменты и практическое применение
Многогранники Пифагора — это удивительная область геометрии, которая открывает множество интересных и полезных идей. На этой странице собраны фотографии, иллюстрации и советы по пониманию правильных многогранников, их применениям в разных сферах, а также ключевые аспекты теории Пифагора. Здесь вы найдете информацию как для учеников, так и для тех, кто интересуется более глубоким изучением геометрии и математических принципов.
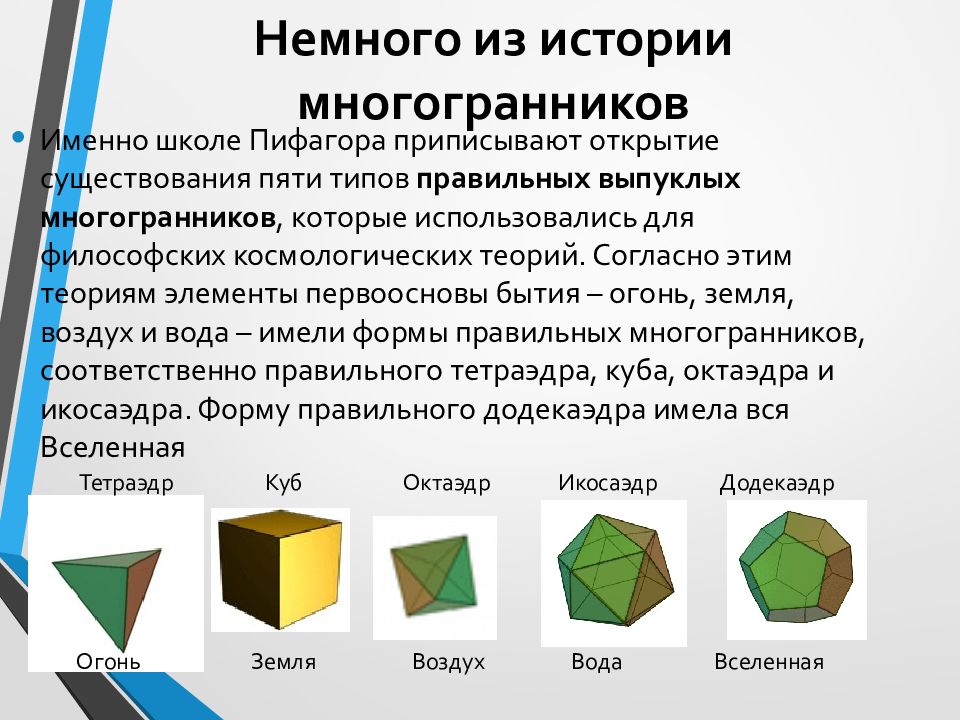

Понимание многогранников начинается с изучения их основных характеристик: вершин, рёбер и граней. Знайте, как они связаны между собой.
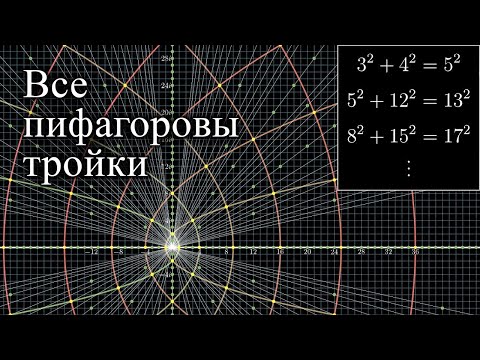
Визуализация всех возможных пифагоровых троек [3Blue1Brown]
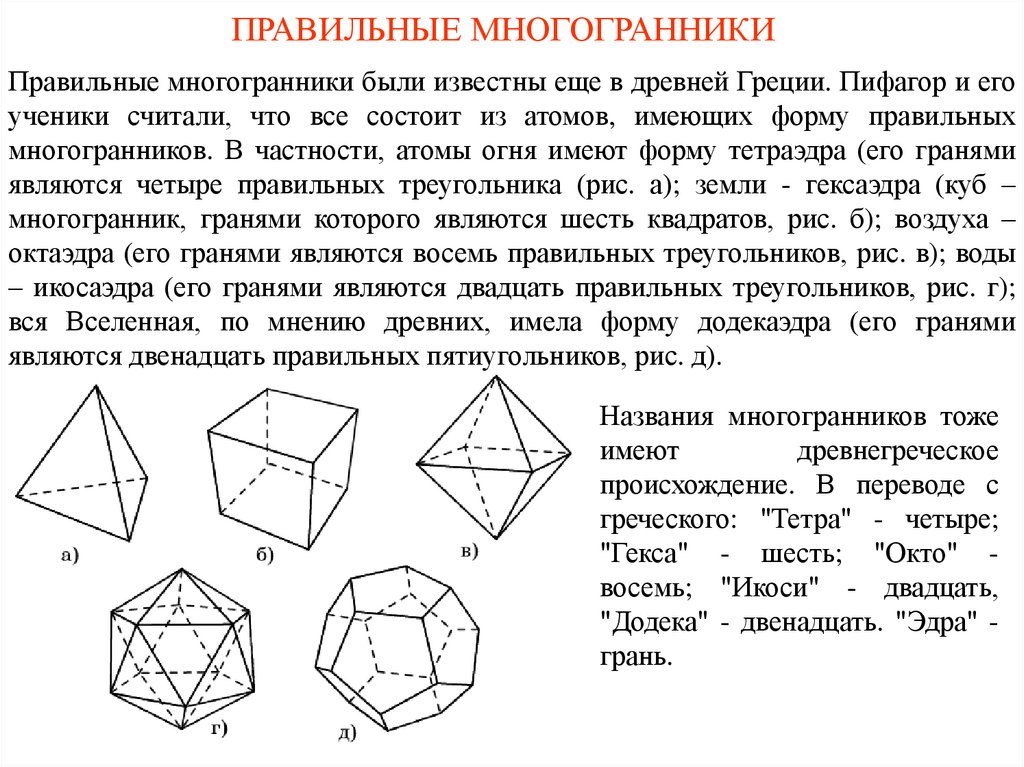
Используйте визуальные инструменты, такие как 3D-модели, чтобы лучше понять структуру многогранников и их симметрию.

Многогранники. Методы решения

Многогранники Пифагора часто встречаются в архитектуре и дизайне, поэтому изучение их свойств поможет вам в практическом применении.
Самая сложная задача из самой сложной олимпиады [3Blue1Brown]

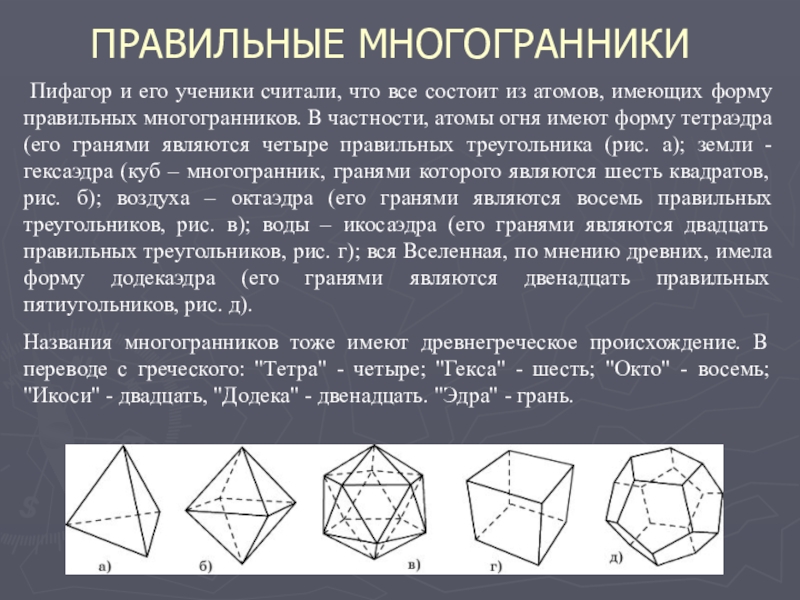
Для лучшего усвоения геометрических свойств правильных многогранников, попробуйте самостоятельно строить их из простых материалов, например, из бумаги.

Видеоурок по математике \

Не забывайте о важности теоремы Пифагора: она помогает понять взаимосвязь между рёбрами и высотами многогранников.

Задача 13. Правильные многогранники - Стереометрия #14 - Инфоурок
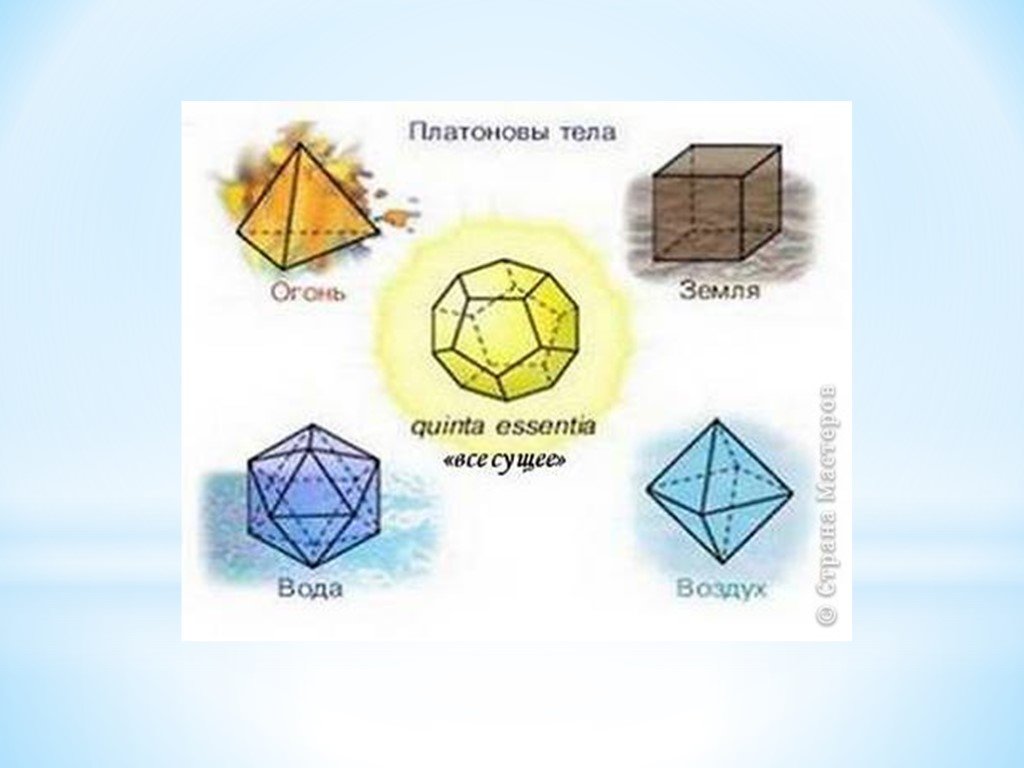

Каждый многогранник имеет уникальную симметрию, изучение которой поможет вам лучше понять его геометрические особенности.
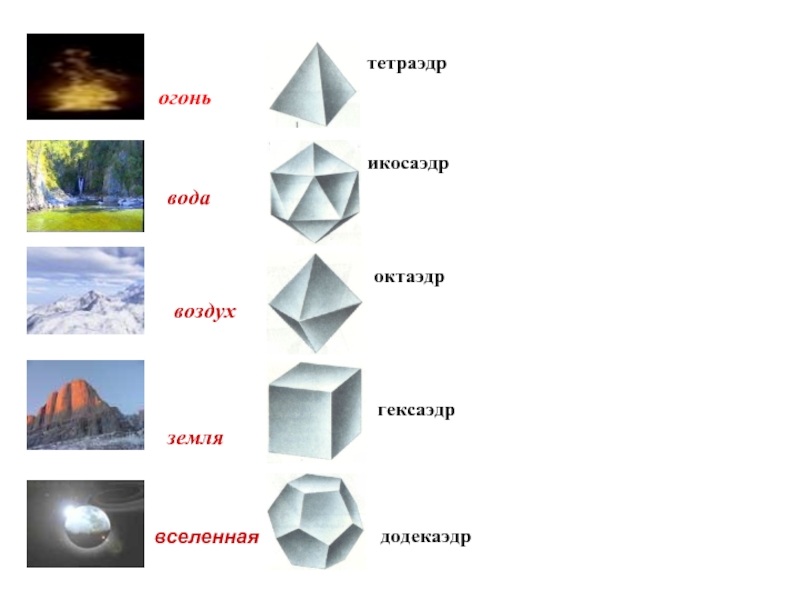

Попробуйте сочетать теорию и практику: рисуйте правильные многогранники на бумаге, чтобы визуализировать их объем и форму.
Применяйте полученные знания для решения задач на нахождение объёмов и площадей многогранников.

Golden icosahedron


Внимательно изучайте многогранники в различных источниках, чтобы понять их историческое значение и роль в науке.

Задача 12. Правильные многогранники - Стереометрия #13 - Инфоурок


Использование математического ПО и симуляторов поможет вам моделировать различные многогранники и изучать их в разных ракурсах.

Тема 9. Правильные многогранники
