Как правильно записывать систему линейных уравнений с использованием матриц
Система линейных уравнений является важным понятием в линейной алгебре, и понимание матричной записи позволяет эффективно решать задачи с помощью методов, таких как метод Гаусса или обратной матрицы. Важно знать, как преобразовать систему в матричную форму для упрощения вычислений и применения алгоритмов для нахождения решений.


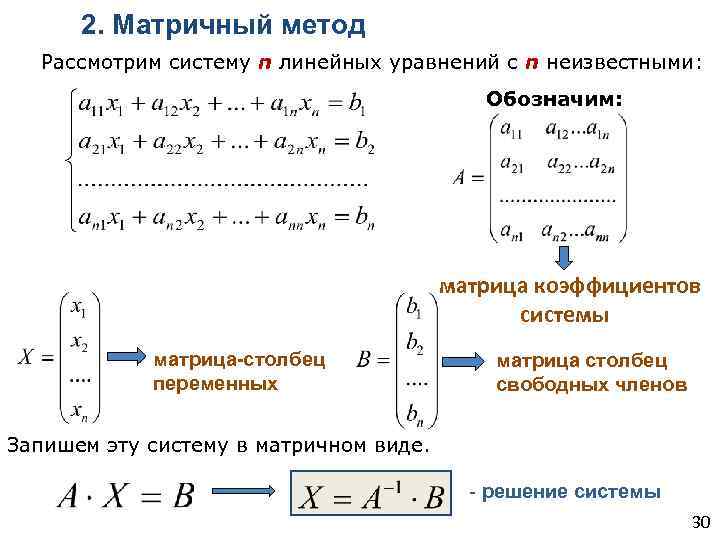
Для успешного применения матричной записи системы линейных уравнений важно правильно понимать структуру коэффициентов и переменных.

метод Гаусса СИСТЕМА ЛИНЕЙНЫХ УРАВНЕНИЙ решение СЛАУ


Использование матричной формы позволяет ускорить решение систем с большим количеством уравнений, что особенно важно в вычислительной математике.
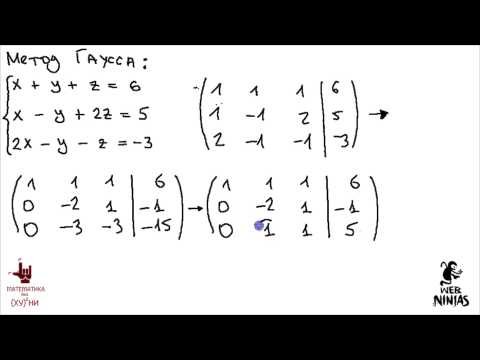
Математика без Ху%!ни. Метод Гаусса.
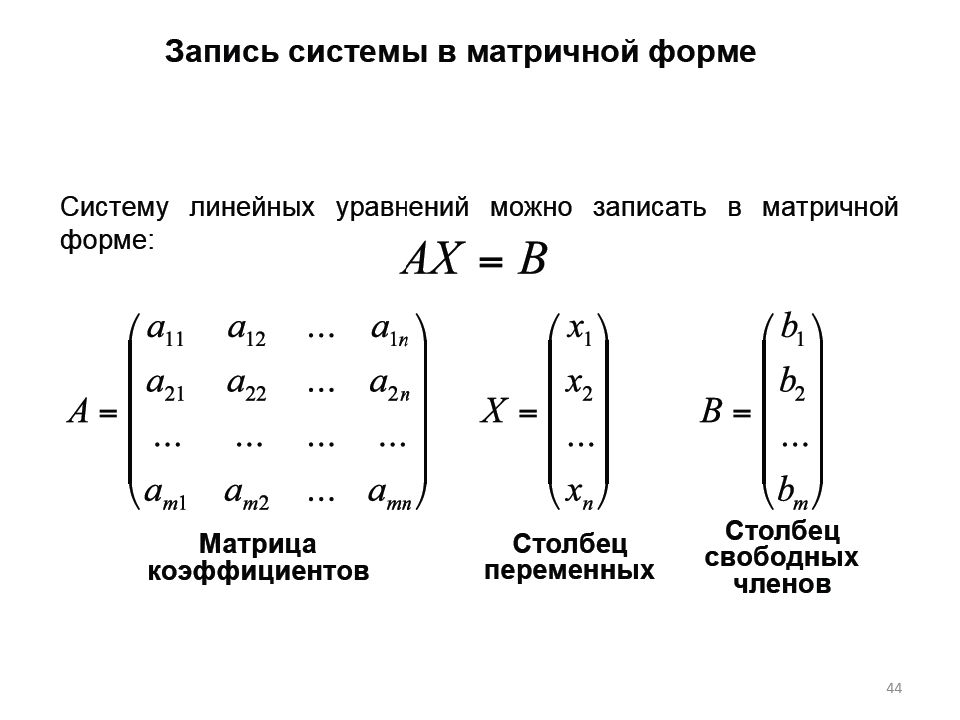

При записи системы уравнений в матричной форме важно учитывать размерность матрицы и её соответствие числу переменных и уравнений.

12. Метод Гаусса решения систем линейных уравнений. Часть 1.


Не забывайте о необходимости проверки детерминанта матрицы коэффициентов, так как его равенство нулю указывает на отсутствие или бесконечность решений.
Файл со всеми формулами к ЕГЭ/ОГЭ в шапке #огэ #онлайншкола #математика #егэ


Для решения системы с помощью матриц используйте методы, такие как обращение матрицы или метод Гаусса, в зависимости от контекста задачи.
Математика Без Ху%!ни. Система линейных уравнений. Метод Крамера.

Обратите внимание на использование расширенной матрицы, которая объединяет коэффициенты и свободные члены уравнений, что упрощает процедуру решения.

Метод Гаусса. Исследование системы на совместность. Несовместная система

Если система имеет бесконечно много решений, это обычно означает, что матрица коэффициентов вырождена, и можно использовать параметры для нахождения общее решение.

15. Однородная система линейных уравнений / фундаментальная система решений
Перед применением метода Гаусса всегда проверяйте систему на линейную независимость уравнений, чтобы избежать ошибочных выводов.

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvy

Математика без Ху%!ни. Метод Гаусса. Совместность системы. Ранг матрицы.

Важно не только уметь записывать систему уравнений в матричной форме, но и интерпретировать полученные результаты для правильного понимания решения задачи.


При решении системы с использованием матриц убедитесь в корректности всех преобразований, так как малейшая ошибка может привести к неправильному ответу.