Урок по нахождению точки пересечения на прямой: шаг за шагом

В этом разделе мы рассмотрим, что такое пересечение на координатной прямой и как правильно найти точку пересечения двух функций. Также будут приведены полезные советы, которые помогут вам разобраться в этом важном аспекте аналитической геометрии.

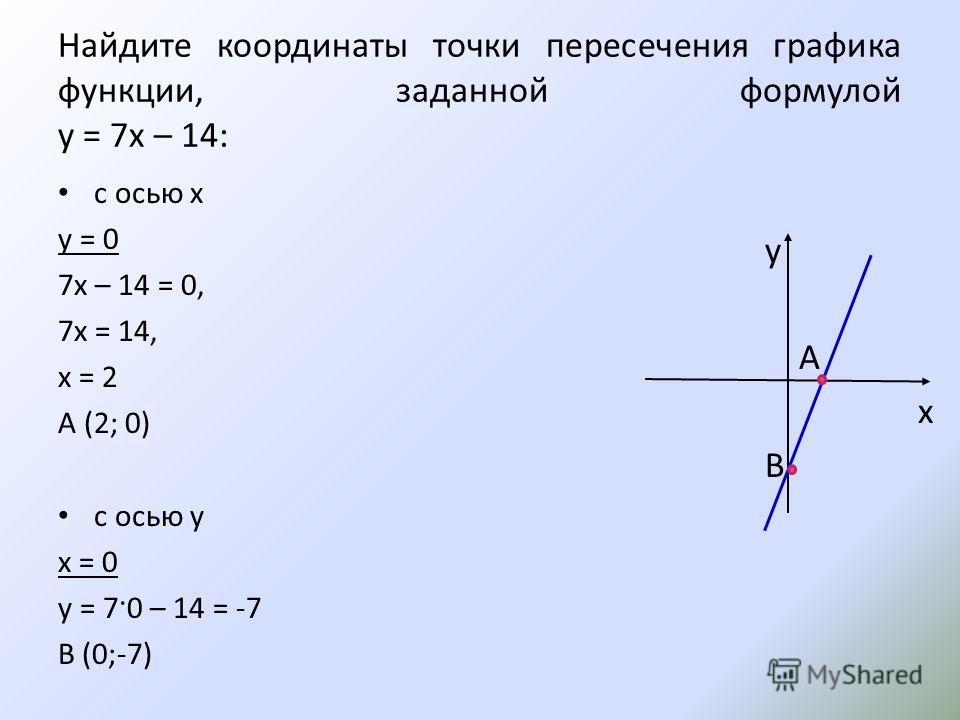
Чтобы найти точку пересечения двух графиков, нужно приравнять их уравнения и решить полученное algebraic уравнение.

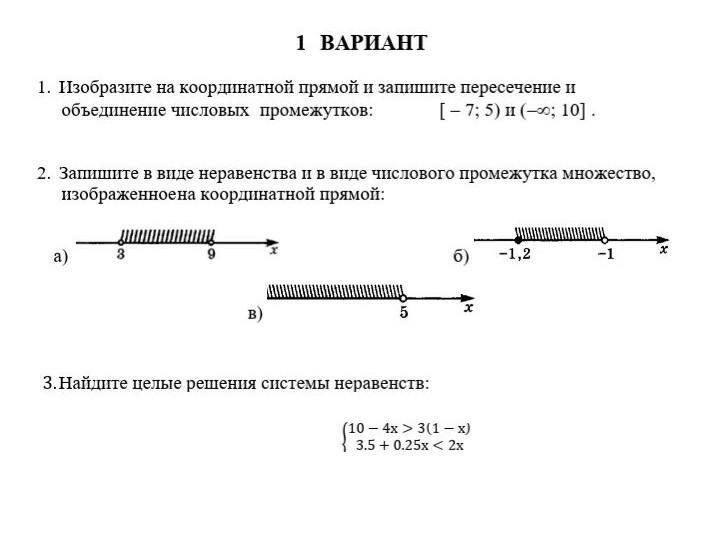
Не забывайте проверять полученные корни на их соответствие исходным уравнениям, особенно если вы работаете с сложными функциями.

Если функции линейные, точка пересечения будет найдена просто через решение системы двух линейных уравнений.

При решении уравнений с квадратными или более сложными функциями важно помнить о возможных дополнительных корнях или исключениях.

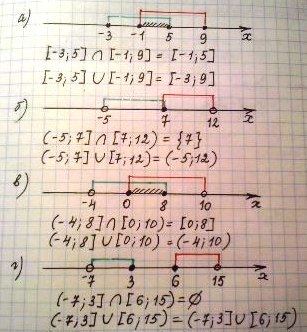
Для визуализации точки пересечения полезно построить графики обеих функций на одной координатной плоскости.

Точка пересечения двух графиков может быть не только реальной, но и комплексной. В этом случае необходимо правильно интерпретировать решение.

При работе с функциями разных типов (например, линейной и квадратичной) может быть полезно использовать методы численного анализа для точного нахождения пересечений.

Не забывайте, что в некоторых случаях функции могут не пересекаться вовсе, если их графики не имеют общих точек.

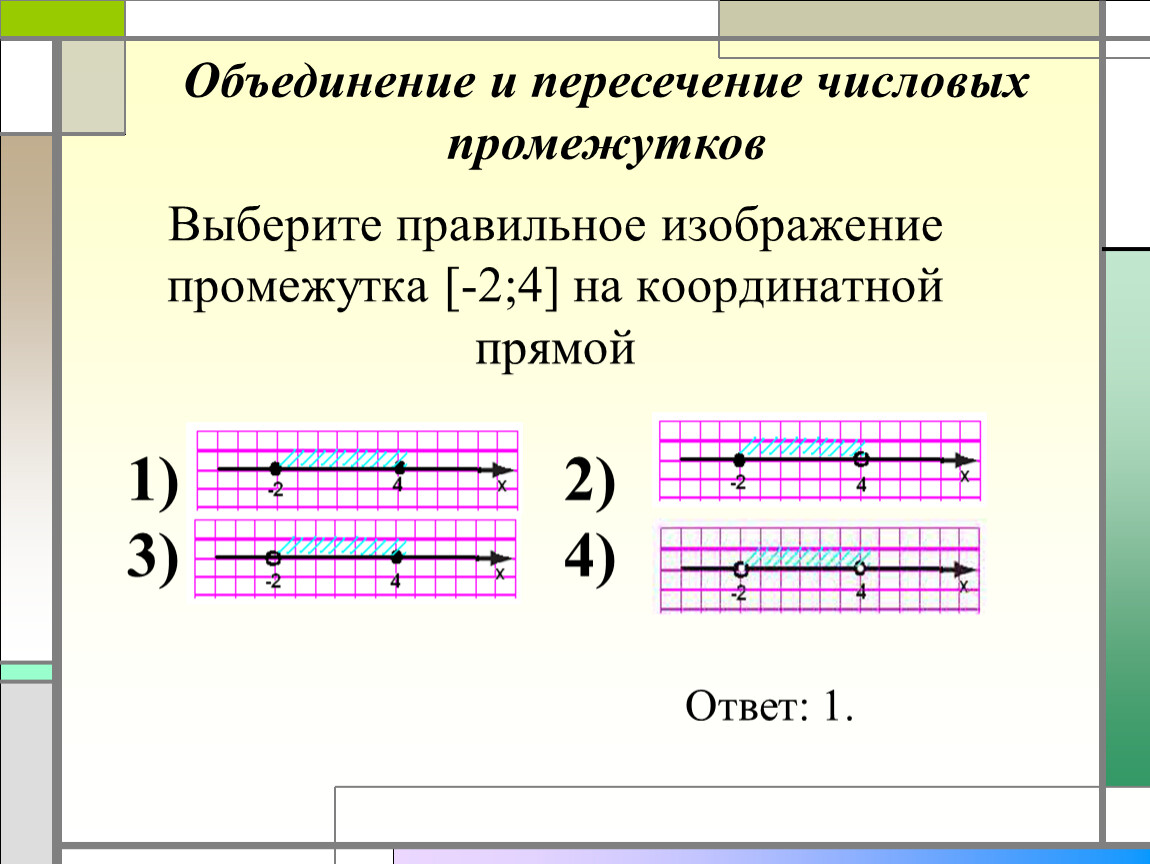
Если у вас есть график и вам нужно найти точку пересечения с другой функцией, попробуйте воспользоваться инструментами динамической геометрии, например, GeoGebra.

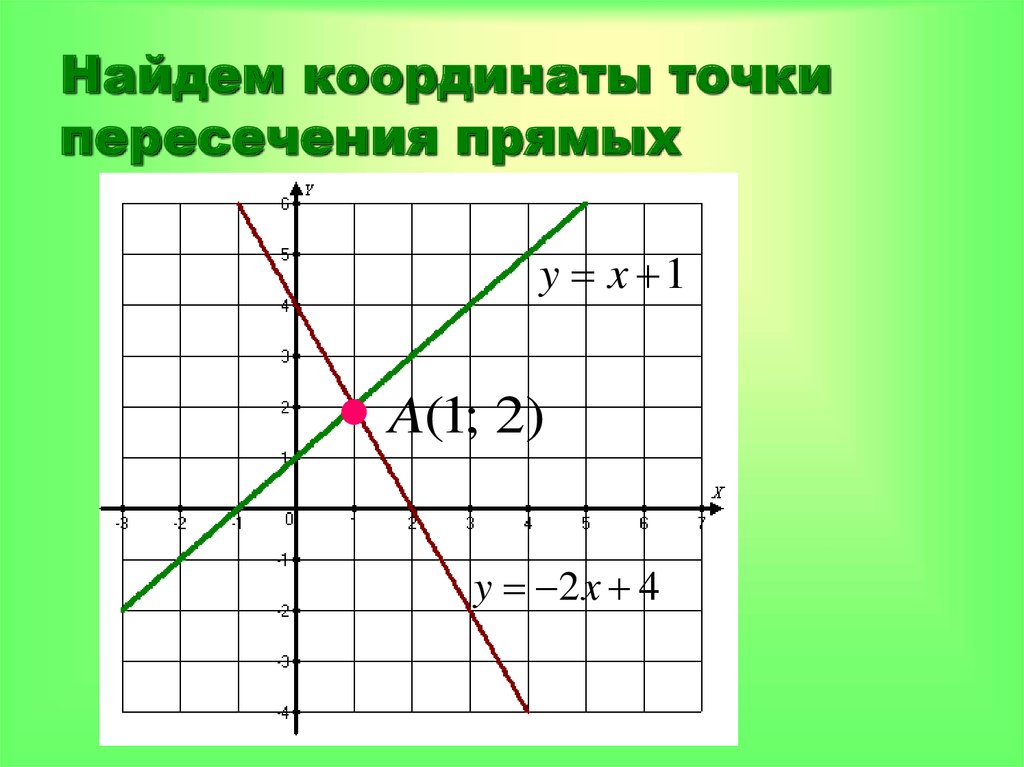
Помимо точного вычисления, полезно понять смысл пересечения: это может быть не только точка, но и решение реальной задачи.