Отрезки касательных и их роль в геометрии вписанных окружностей
В этой статье мы разберем, что такое отрезки касательных к вписанной окружности, как их находить и какие важные геометрические свойства они имеют. Вы найдете полезные советы и практические рекомендации для работы с касательными.
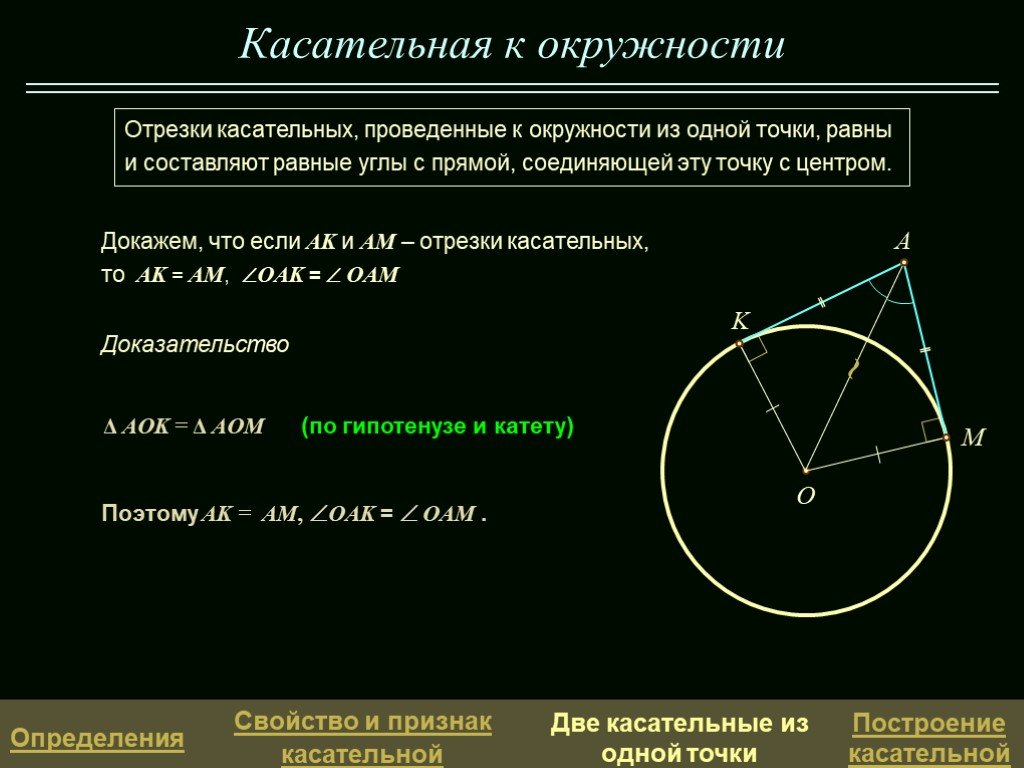
Для нахождения отрезков касательных к вписанной окружности можно использовать теорему о касательных, которая утверждает, что касательные, проведенные из одной точки к окружности, равны между собой.

Всё про углы в окружности. Геометрия - Математика

Если вам нужно вычислить длину отрезка касательной, воспользуйтесь формулой: длина касательной равна корню из разности квадратов расстояния от точки до центра окружности и радиуса окружности.

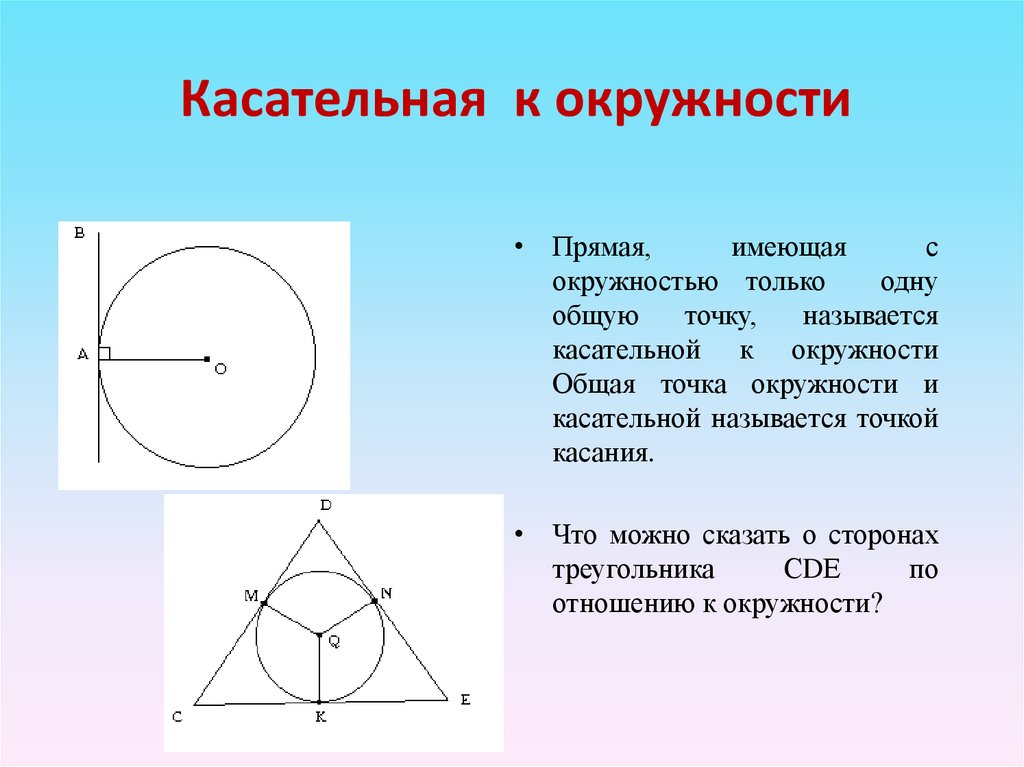
Урок по теме КАСАТЕЛЬНАЯ К ОКРУЖНОСТИ
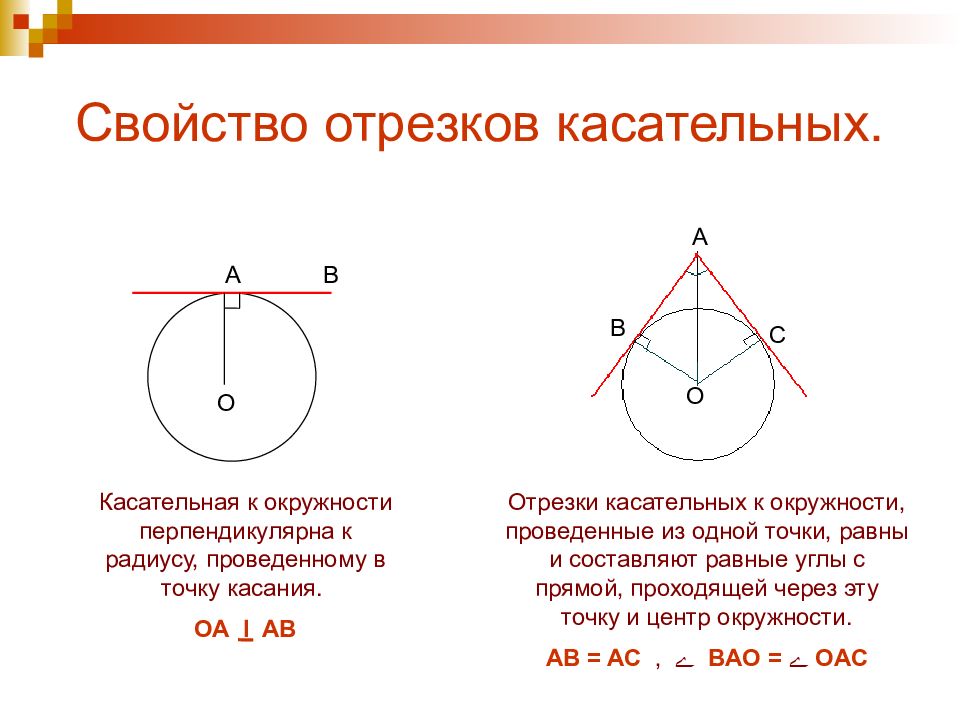
Важным свойством касательных является то, что они пересекаются под прямым углом с радиусом окружности в точке касания.
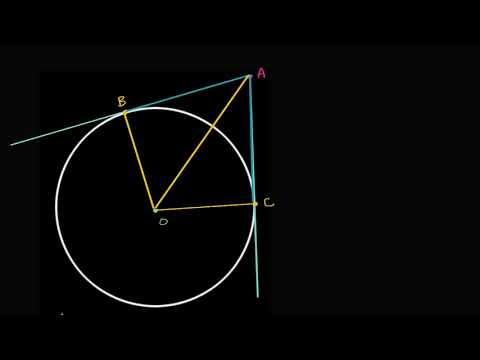
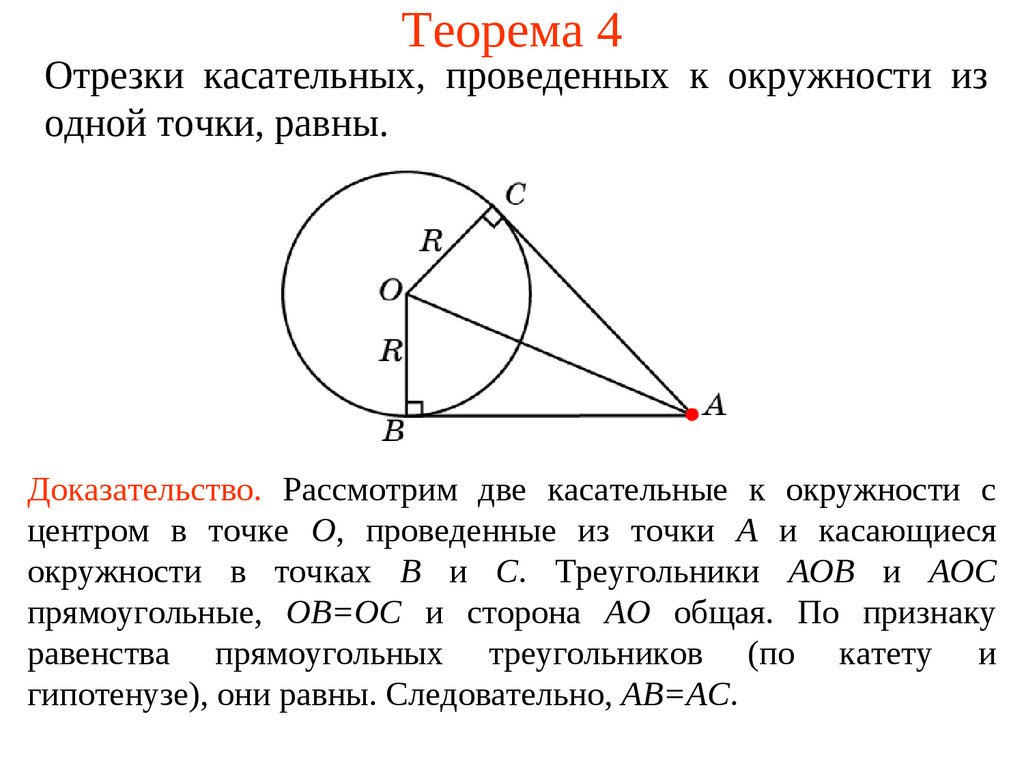
Отрезки касательных из одной точки до точек касания окружности равны - Окружность - Геометрия
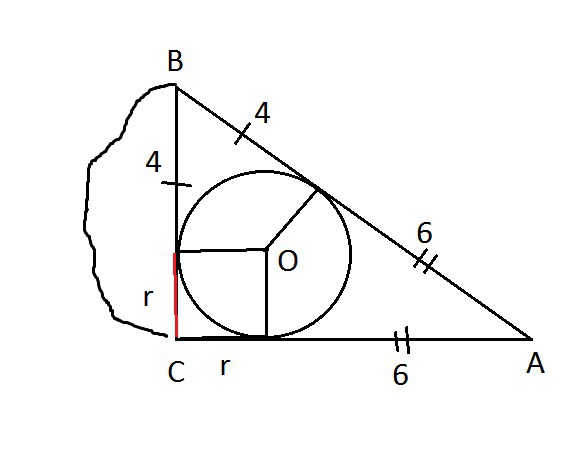
При работе с задачами на касательные важно помнить, что они всегда одинаковы по длине, если они исходят из одной и той же внешней точки.

Геометрия, 9 класс - Касательная к окружности
Используйте геометрические конструкции и чертежи, чтобы визуализировать расположение касательных и лучше понять их взаимосвязь с окружностью.

Доказательство теоремы об отрезках касательных.

Если на плоскости присутствует несколько касательных к окружности, то их углы пересечения и точки касания могут подчиняться интересным симметричным закономерностям.
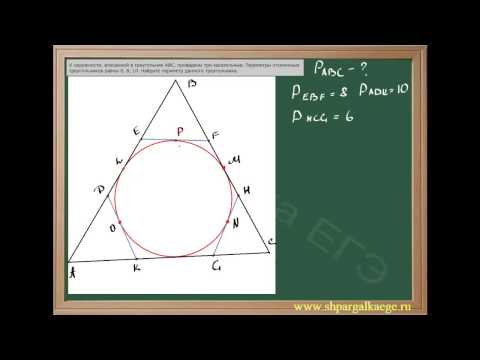
Задание В6 по математике.
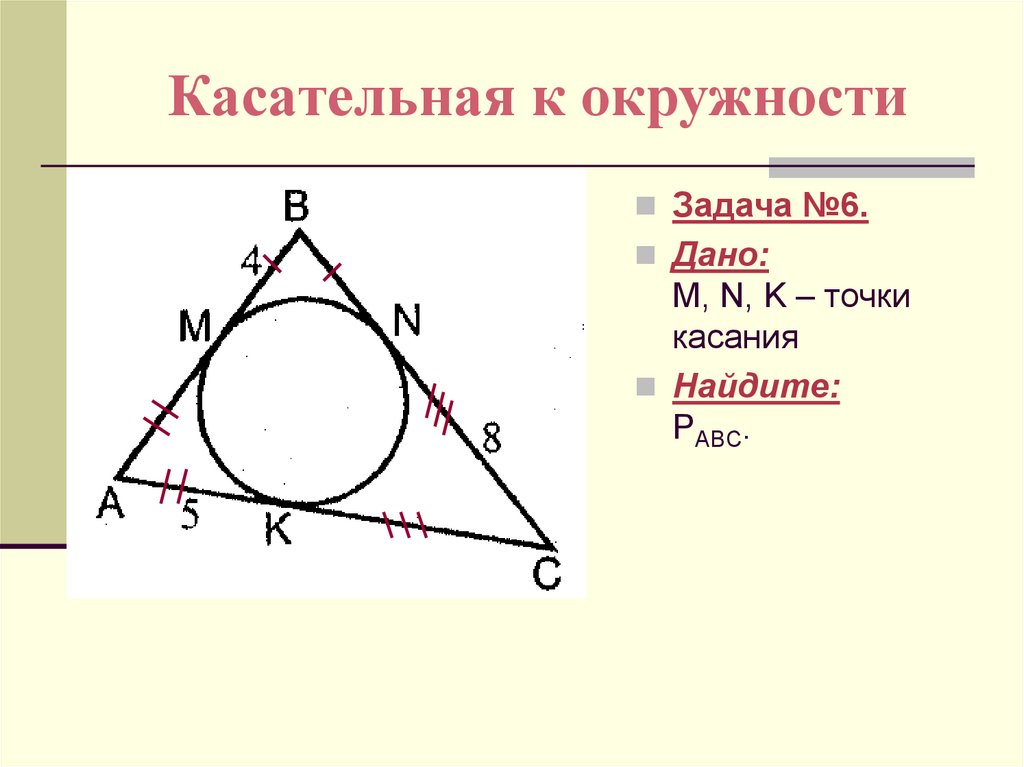
Для решения задач на касательные полезно разбираться в таких понятиях, как эксцентриситет и длина отрезка, соединяющего точку касания с внешней точкой.
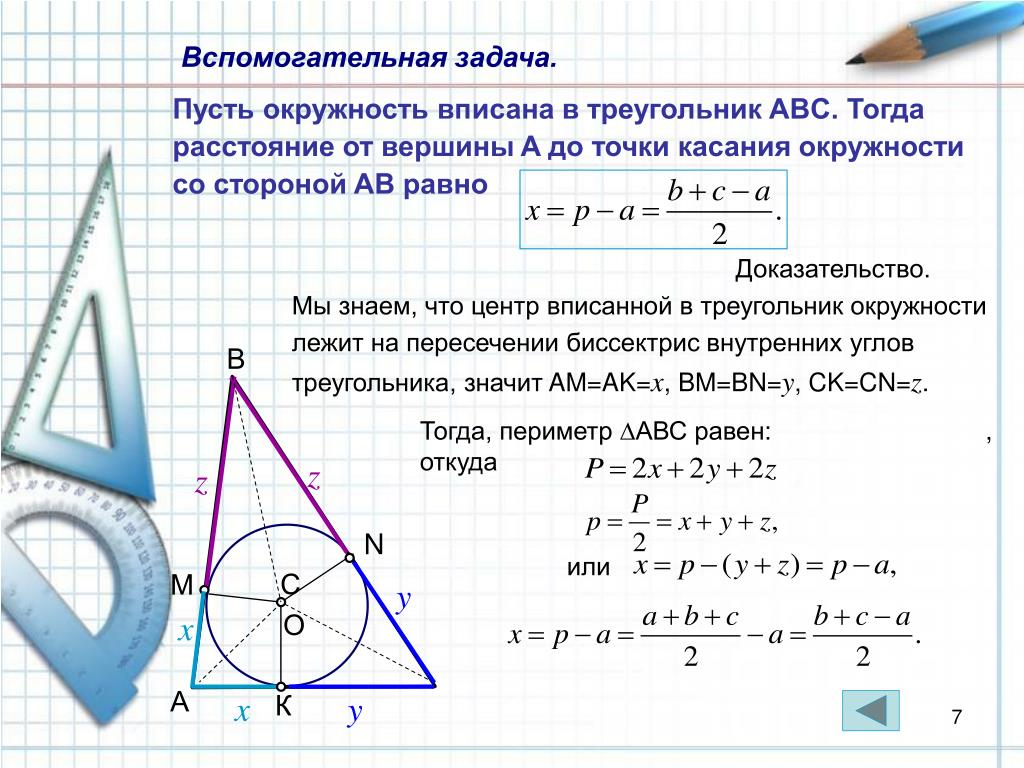

Не забывайте, что отрезки касательных можно использовать для нахождения других важных элементов в геометрических задачах, таких как углы и площади.

№641. Отрезки АВ и АС являются отрезками касательных к окружности с центром О, проведенными из
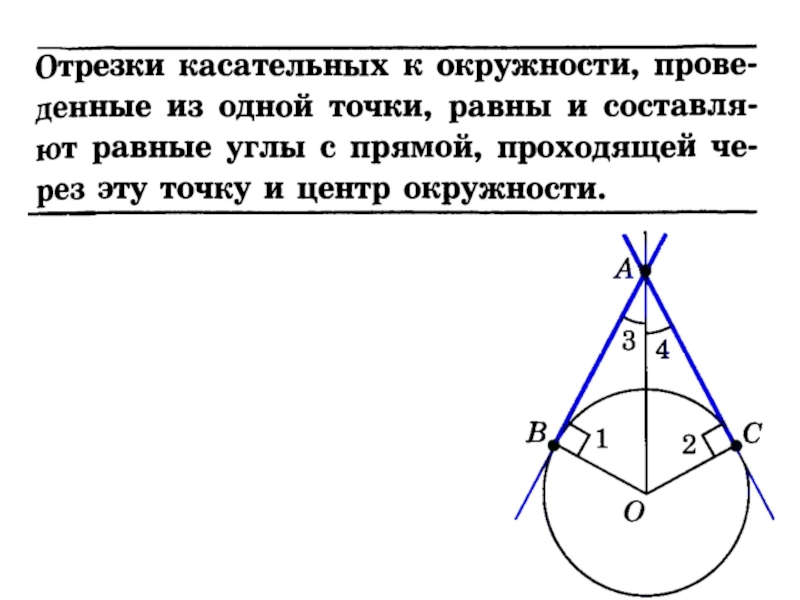
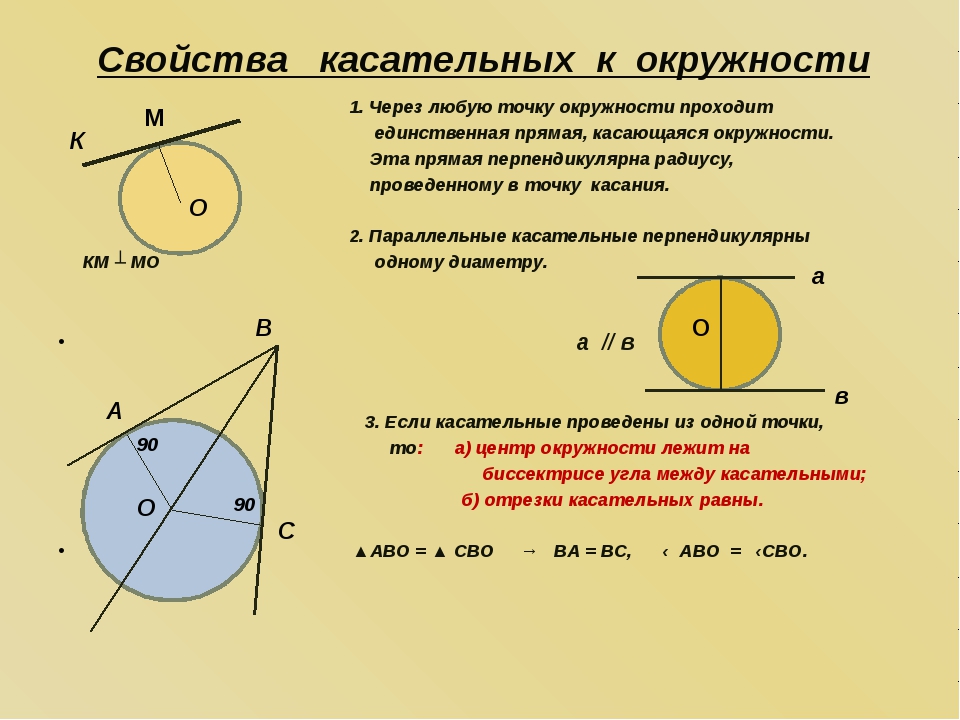
При работе с кругами и окружностями полезно использовать известные формулы для отрезков касательных, чтобы быстро получать результаты и анализировать различные ситуации.

Математика - 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачи

Задачи на касательные к окружности могут включать различные подходы, такие как использование теоремы Пифагора или методов аналитической геометрии для вычисления координат и длин отрезков.

Найдите площадь треугольника на рисунке ★ Два способа решения