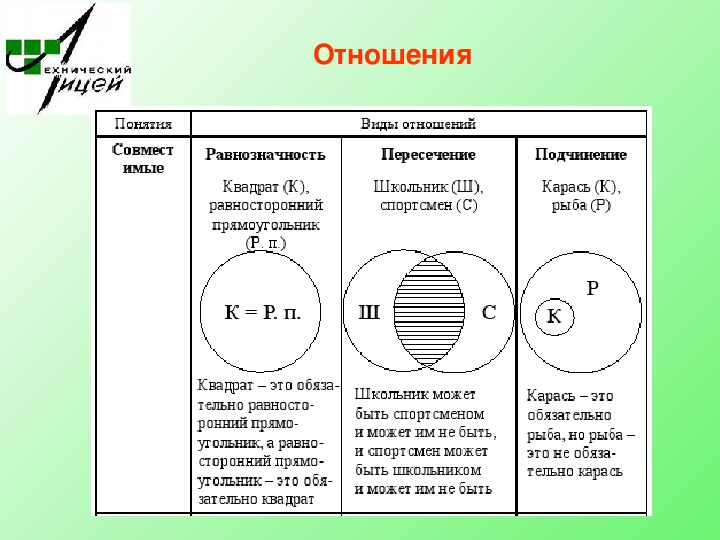
Как правильно использовать круги Эйлера для отображения взаимосвязей множеств
Круги Эйлера — это мощный инструмент для визуализации взаимосвязей между множествами. С помощью них можно наглядно представить пересечения, объединения и различия между объектами, что облегчает понимание сложных концепций в математике и других областях. Этот раздел содержит полезные советы для эффективного использования кругов Эйлера.
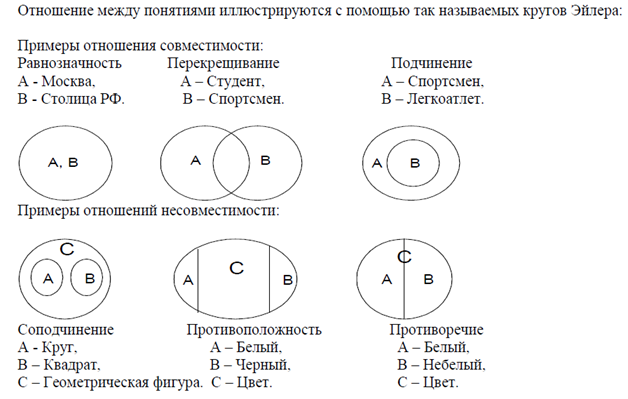
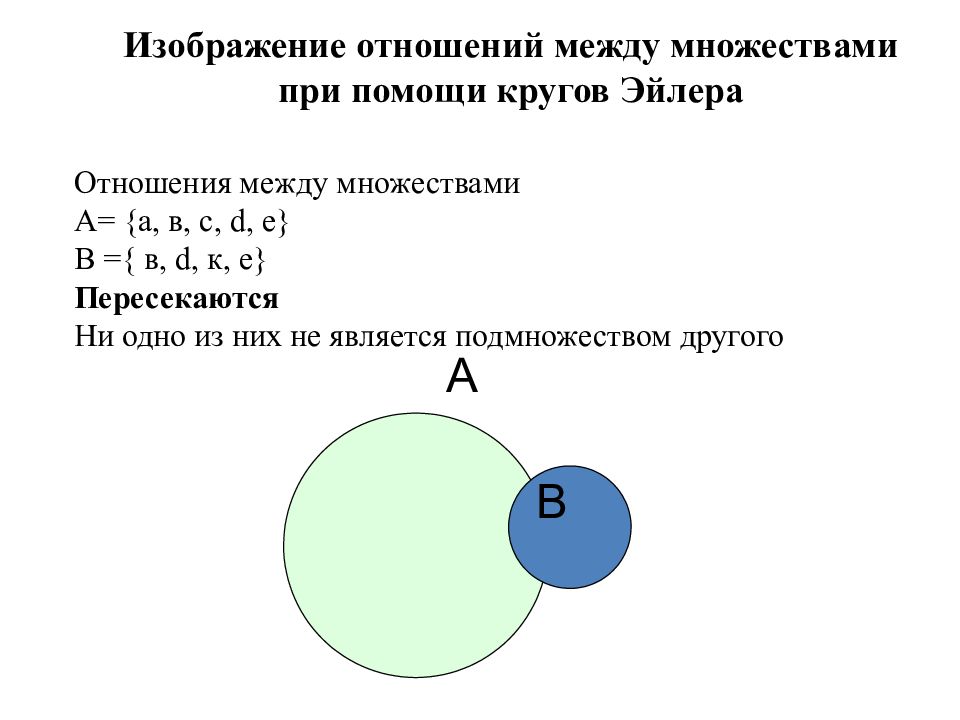

Для более наглядного представления используйте цветовые схемы для различных множеств, чтобы легко различать их пересечения.

Логика. Основы Логики. Логическое Мышление
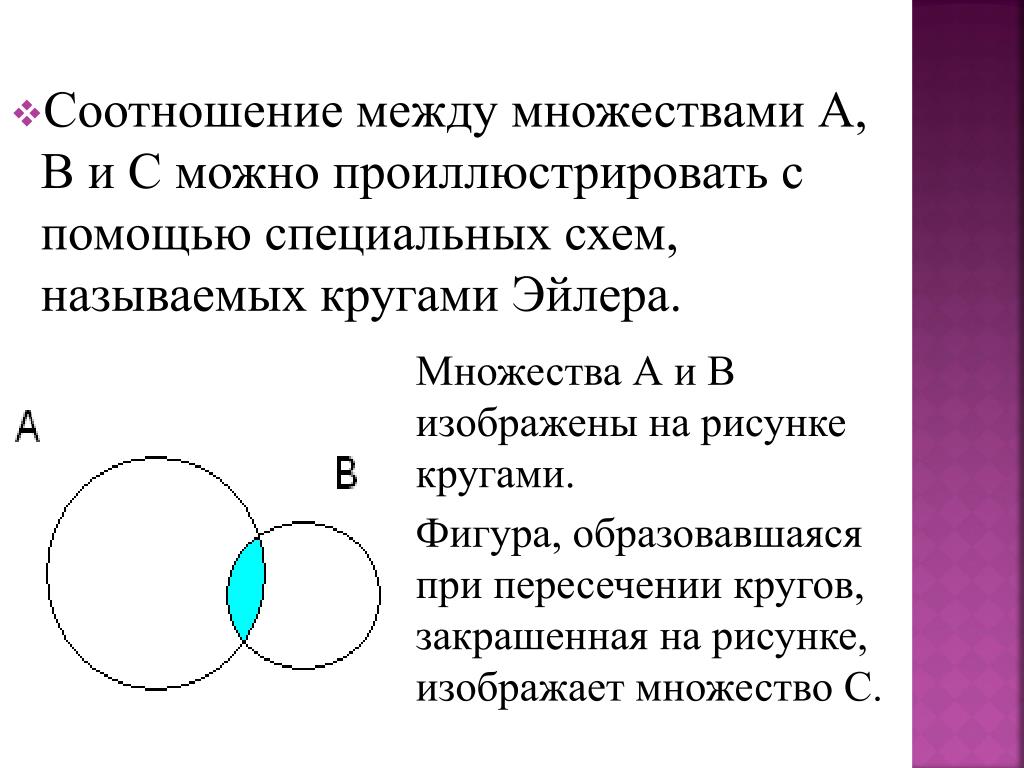
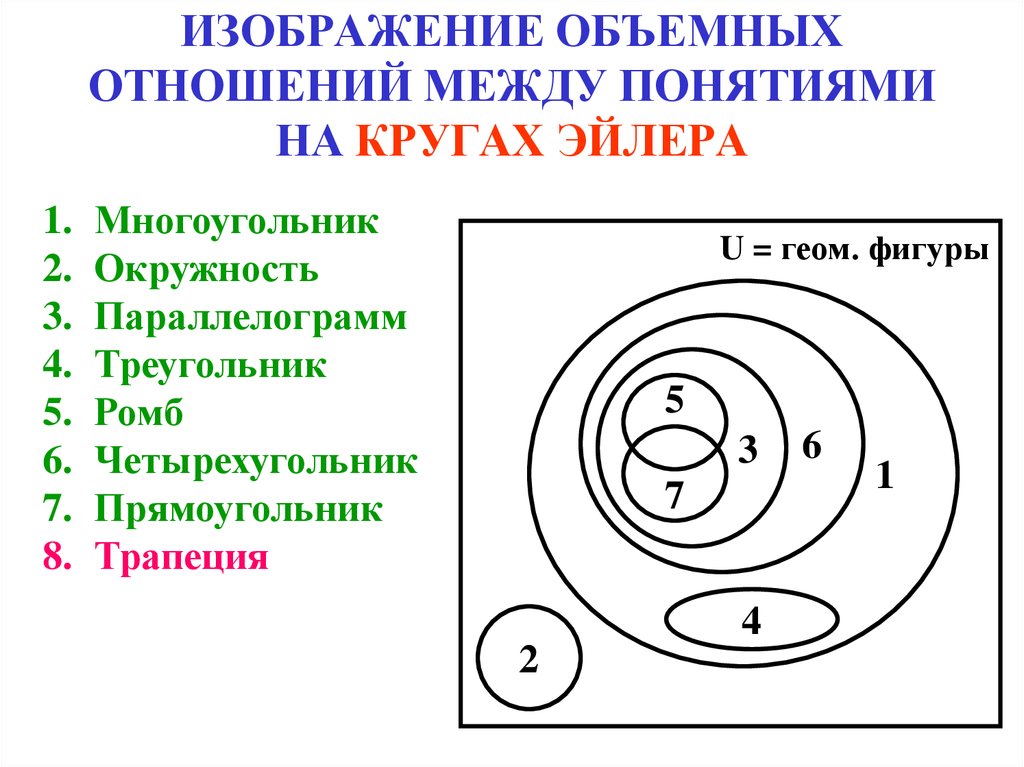
Когда работаете с несколькими множествами, старайтесь избегать слишком сложных диаграмм. Простота — ключ к пониманию.

Круги Эйлера в реальной жизни. Математика на QWERTY
Проверяйте каждое пересечение на корректность, чтобы избежать ошибок при анализе множества.
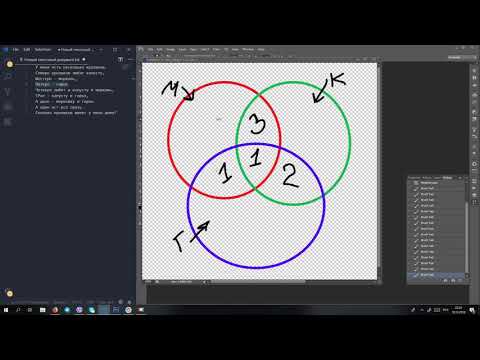
Простое объяснения решения задач при помощи кругов Эйлера
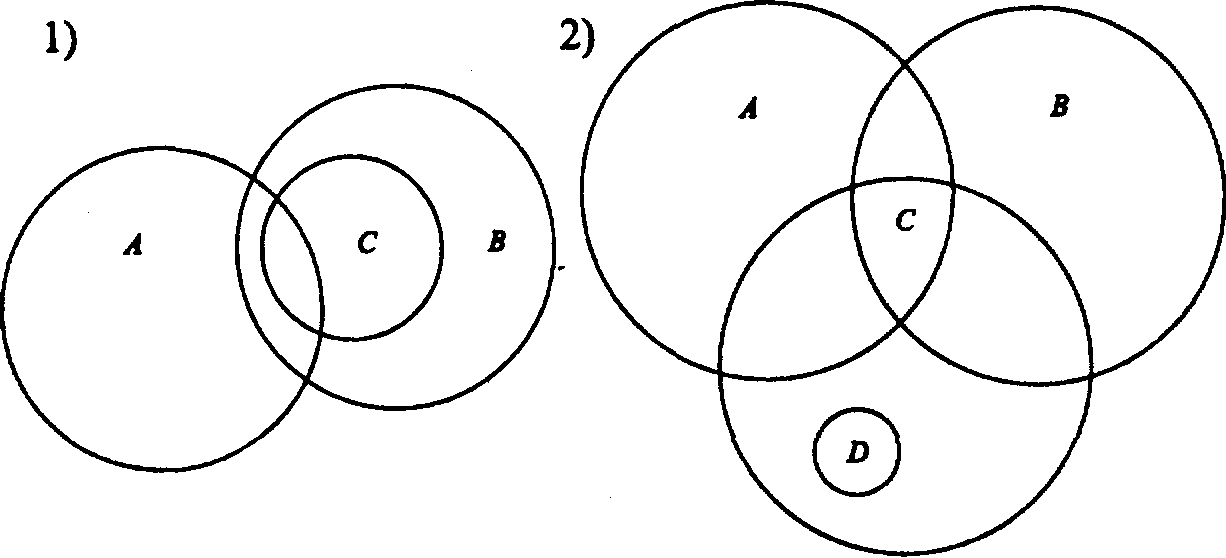
Для множества с большим количеством элементов используйте дополнительные подписи и легенды, чтобы сделать диаграмму более информативной.

Подмножество. Операции над множествами (пересечение, объединение множеств) – 8 класс алгебра

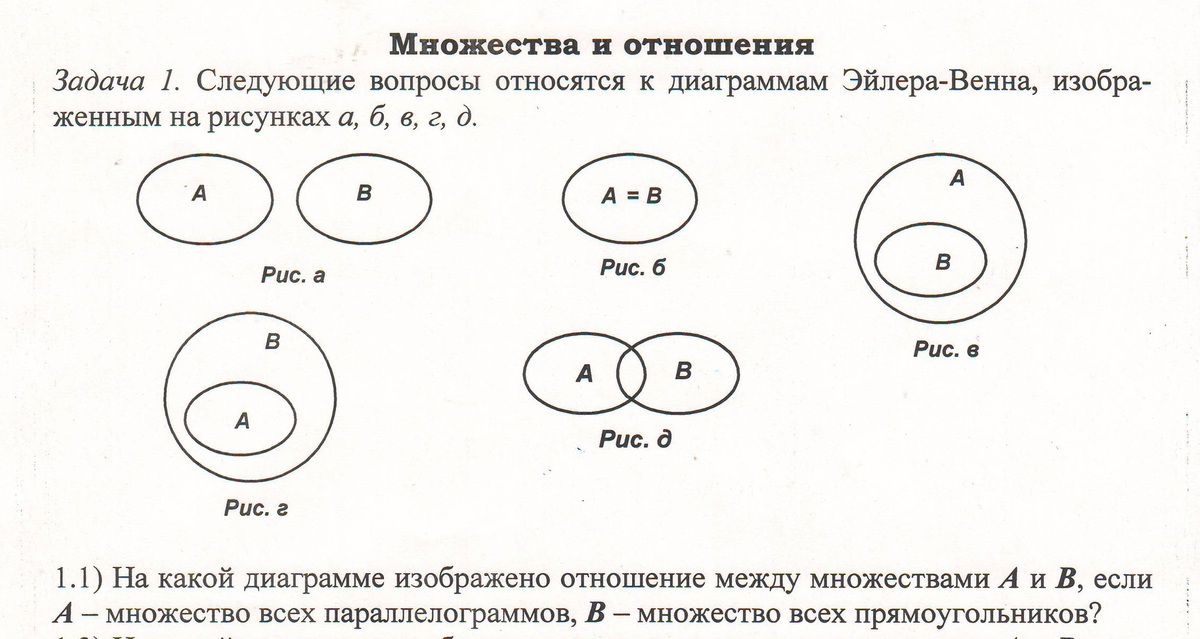
Обратите внимание на плотность пересечений. Если их слишком много, рассмотрите возможность деления множества на подмножества.

Круги Эйлера за 3 минуты - ОГЭ по информатике 2024
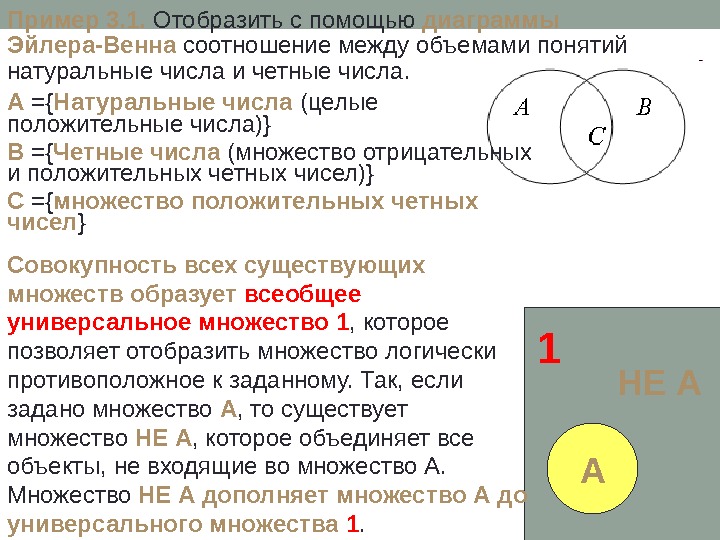
Используйте разные стили линий (сплошные, пунктирные и т.д.) для обозначения различных типов отношений между множествами.
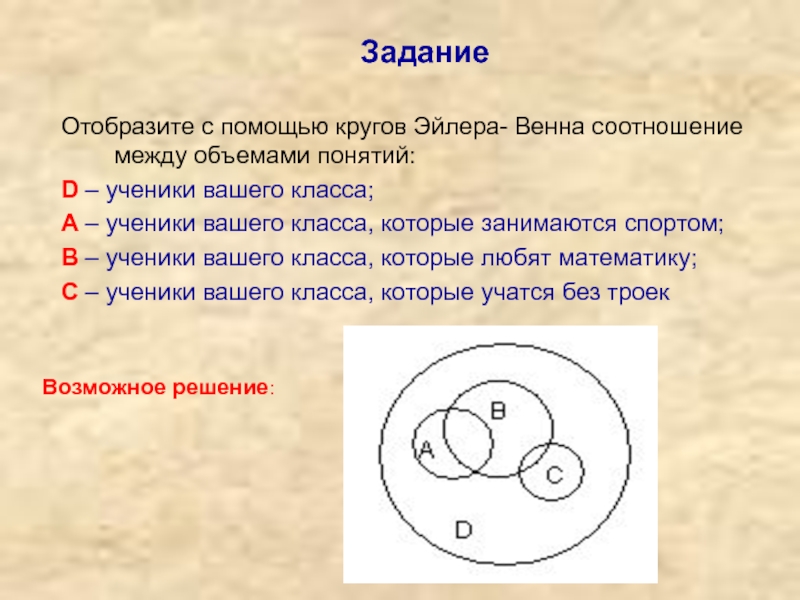
Практикуйтесь на простых примерах с двумя или тремя множествами перед тем, как перейти к более сложным случаям.
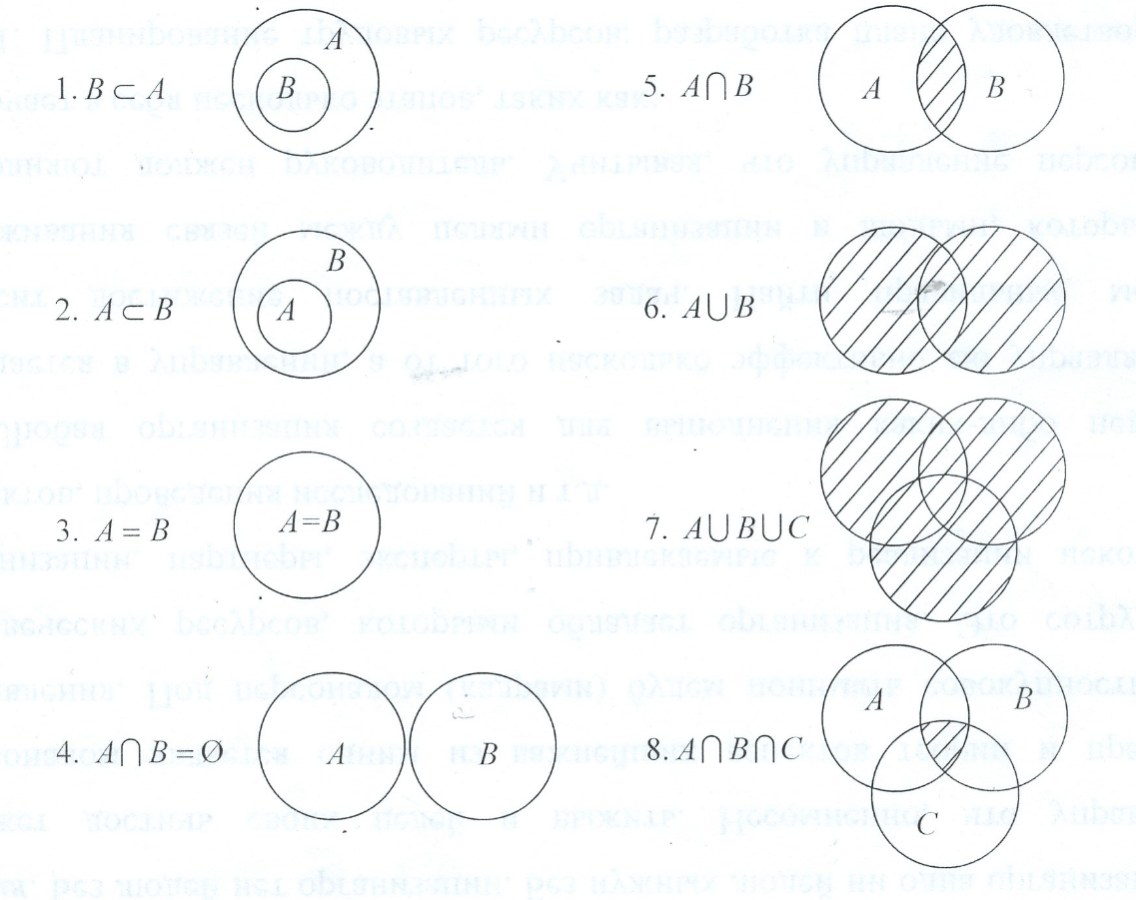

Если диаграмма кажется слишком сложной, попробуйте разделить задачу на несколько более простых частей и проанализировать каждую по отдельности.
Используйте интерактивные инструменты для создания кругов Эйлера, чтобы облегчить их редактирование и улучшить восприятие.
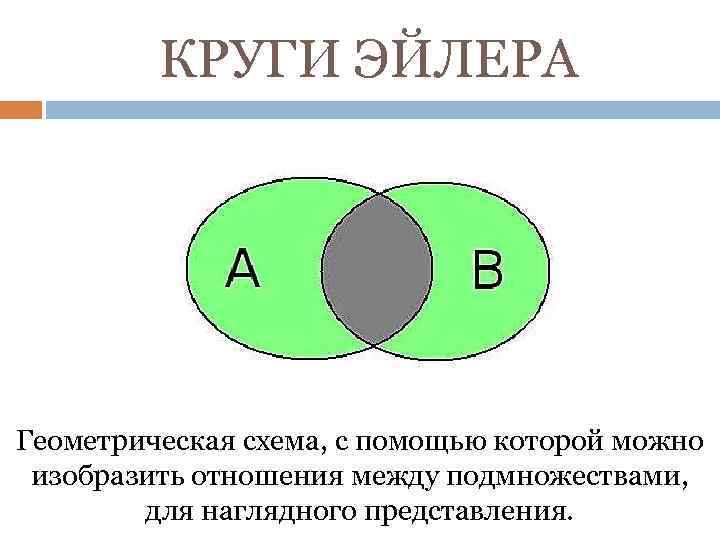
Не забывайте, что круги Эйлера могут быть полезны не только в математике, но и в области логики, информатики и других дисциплин.