Понимание ориентированных и взвешенных графов: ключевые моменты для работы с графами и деревьями

Ориентированные и взвешенные графы являются важными концепциями в теории графов, которые широко применяются в различных областях математики и информатики. Знание основ их структуры и особенностей позволяет эффективно решать задачи оптимизации, маршрутизации и анализа данных. В этой подборке представлены основные принципы работы с такими графами и полезные советы для их использования.

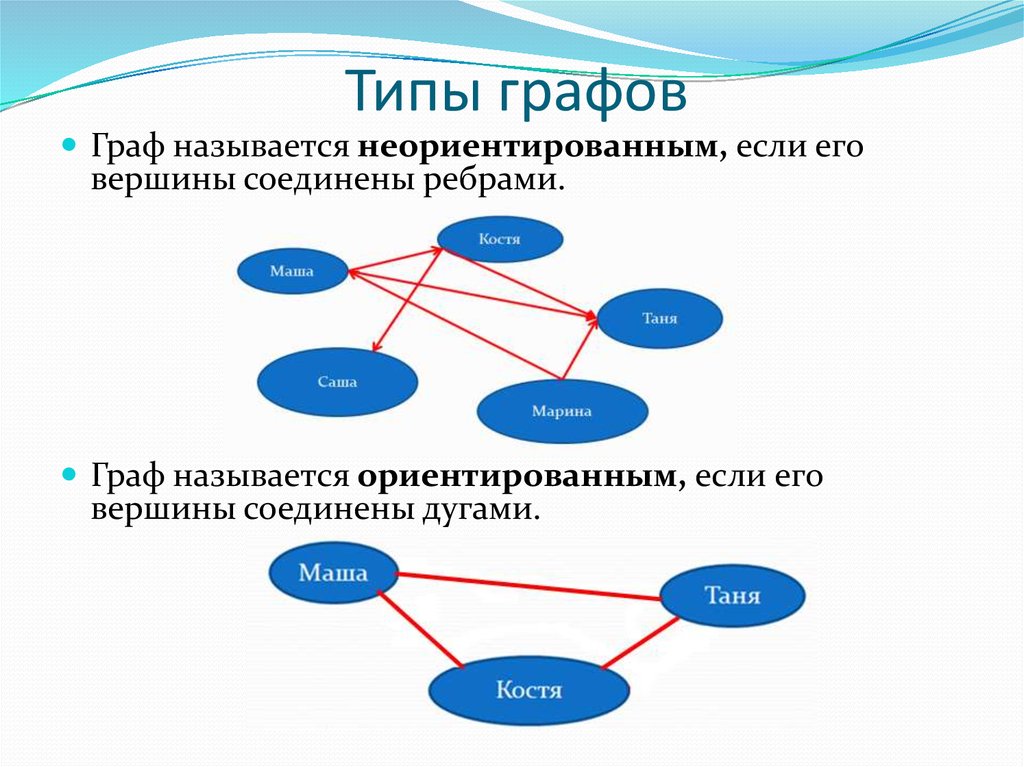
Ориентированные графы часто применяются в задачах, где важен порядок следования объектов, например, в сети или на дорогах.

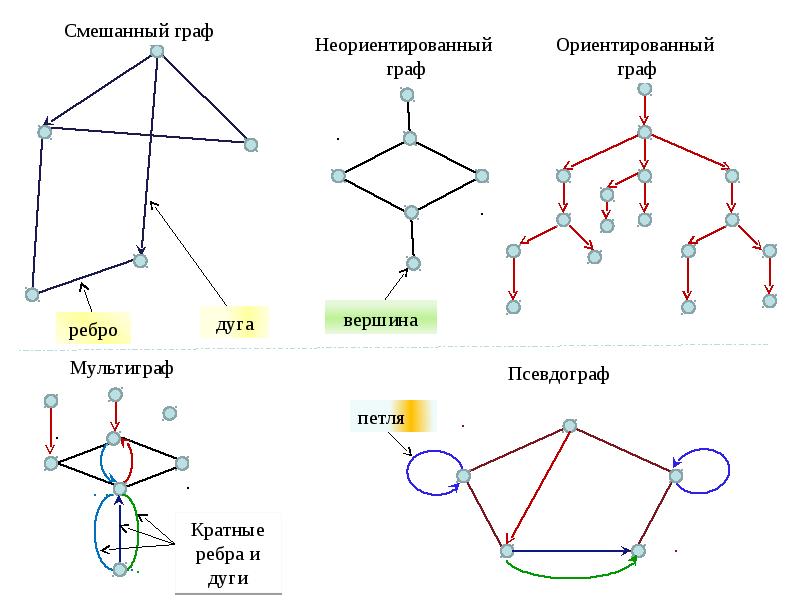
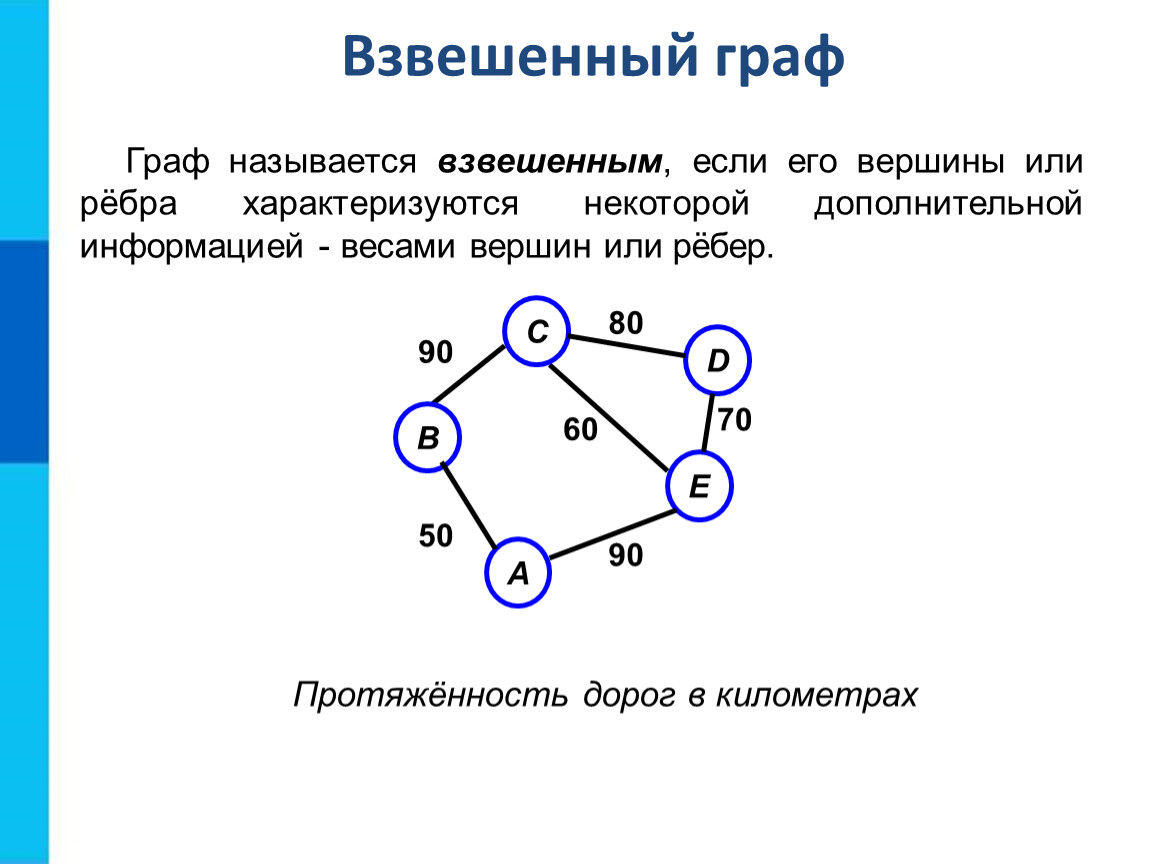
Взвешенные графы полезны, когда необходимо учитывать стоимость или расстояние между вершинами, например, в задаче нахождения кратчайшего пути.

Для работы с деревьями важно помнить, что дерево – это частный случай графа, где нет циклов и существует один путь между любыми двумя вершинами.

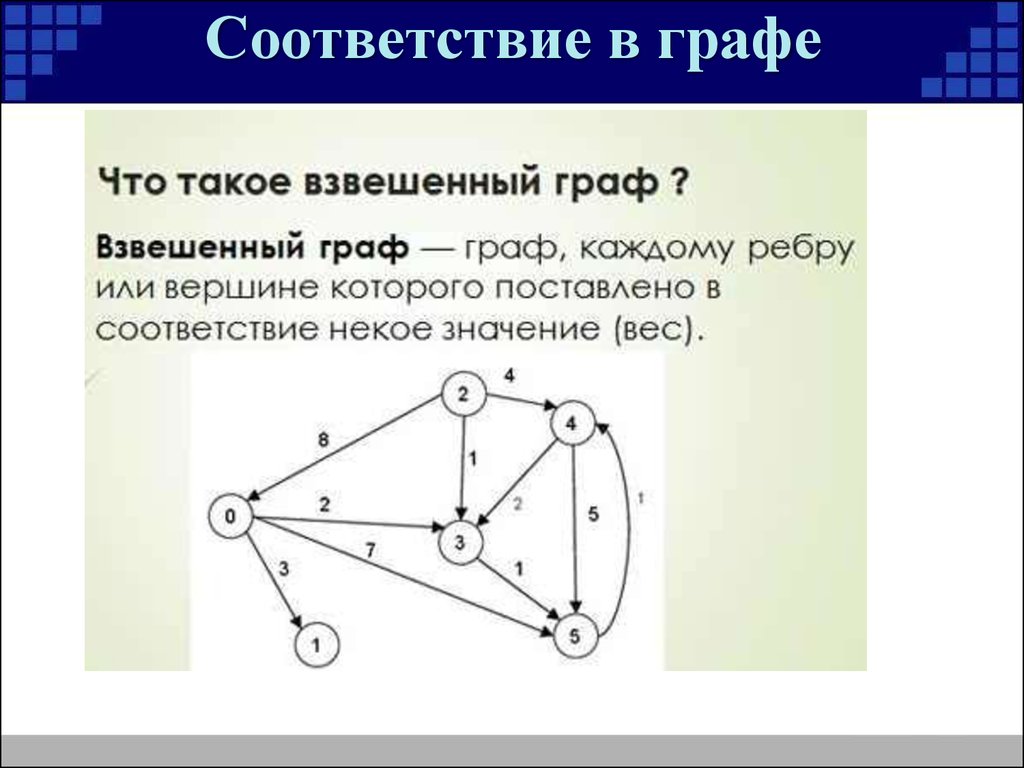
Если в графе есть циклы, это может существенно усложнить задачи поиска маршрутов и оптимизации. Важно учитывать этот момент при проектировании графа.

При построении ориентированных графов стоит обратить внимание на направление рёбер, которое определяет направленность связи между объектами или действиями.

При анализе взвешенных графов полезно использовать алгоритмы поиска кратчайшего пути, такие как алгоритм Дейкстры или алгоритм Беллмана-Форда.

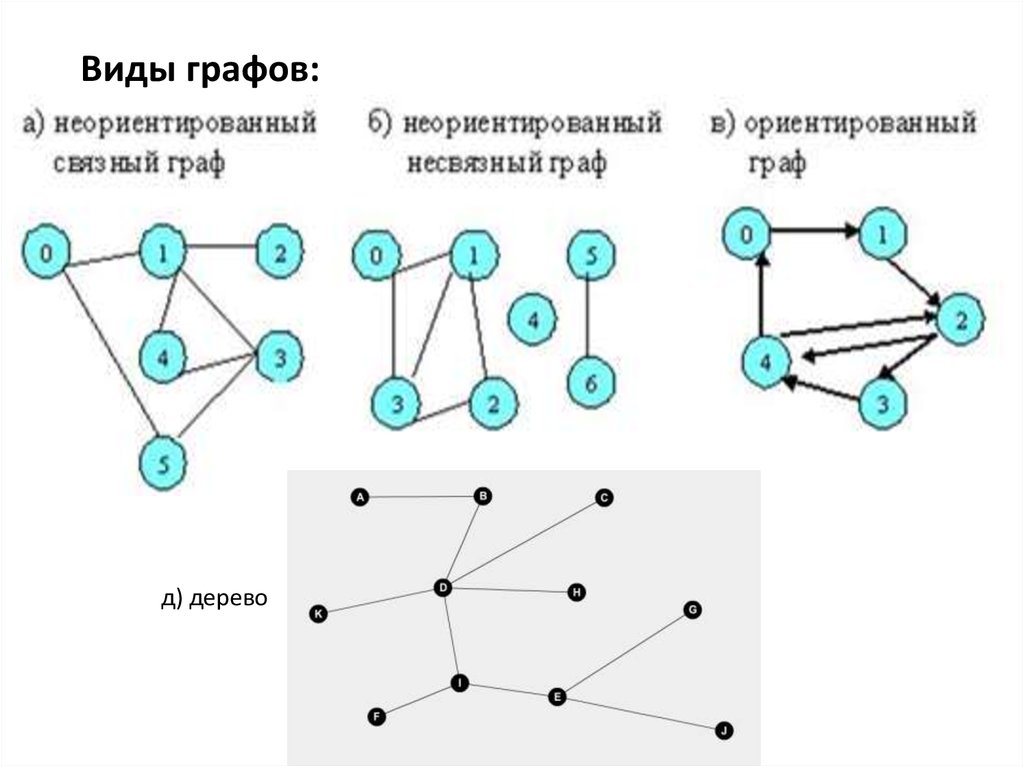
Деревья часто используются для моделирования иерархий, таких как файловые системы или структуры данных, например, двоичные деревья поиска.

Для эффективного поиска путей в ориентированных графах важно учитывать, что направление рёбер может изменить поведение алгоритмов поиска.

Взвешенные графы могут быть использованы в различных областях, таких как логистика, маршрутизация и моделирование сетей, где учитываются разные стоимости рёбер.

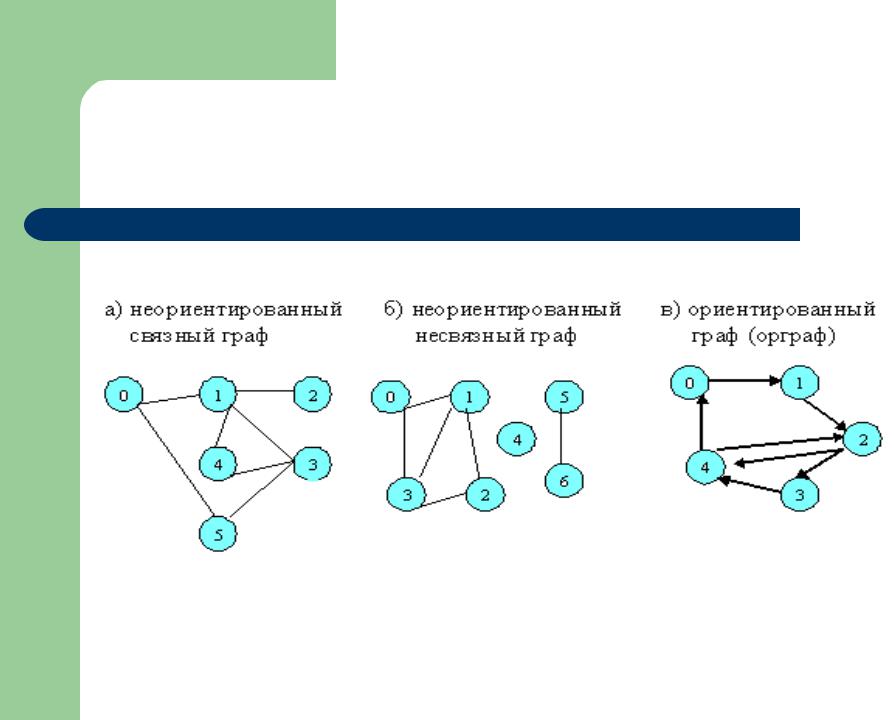
При работе с графами важно также учитывать их структуру: например, можно использовать матрицы смежности или списки смежности в зависимости от задачи.