Пошаговое руководство по нахождению общего решения системы линейных уравнений
На этой странице вы найдете подробное объяснение того, как найти общее решение системы линейных уравнений, а также полезные советы и формулы, которые помогут вам успешно решать задачи по этой теме. Использование правильных методов и подходов значительно упростит процесс вычислений и повысит вашу уверенность в математике.


Для нахождения общего решения системы линейных уравнений важно правильно выбрать метод: метод подстановки, метод исключений или метод Крамера, в зависимости от конкретной задачи.

Общее, частное, базисное решение системы линейных уравнений Метод Гаусса

Перед началом решения проверьте систему на совместность — если система несовместна, то решения не существует.

Самый короткий тест на интеллект Задача Массачусетского профессора

При использовании метода подстановки выражайте одну переменную через другую и подставляйте в оставшиеся уравнения для упрощения системы.

Решение системы уравнений методом Крамера.

Для применения метода Крамера убедитесь, что определитель системы не равен нулю, иначе система не имеет единственного решения.

метод Гаусса СИСТЕМА ЛИНЕЙНЫХ УРАВНЕНИЙ решение СЛАУ

Если в системе присутствуют параметры, используйте их для нахождения общего решения в виде зависимых переменных.

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvy


Для правильного использования метода исключений, выбирайте такое уравнение, из которого проще выразить одну переменную.

Метод Гаусса. Исследование системы на совместность. Несовместная система

При решении системы линейных уравнений с несколькими переменными всегда проверяйте, не появились ли избыточные или противоречивые уравнения.

В случае системы с параметрами всегда учитывайте, что значение параметра может изменить тип решения (единственное, бесконечно много решений или отсутствие решений).
Файл со всеми формулами к ЕГЭ/ОГЭ в шапке #огэ #онлайншкола #математика #егэ

Не забывайте проверять полученные решения, подставляя их обратно в исходную систему уравнений.
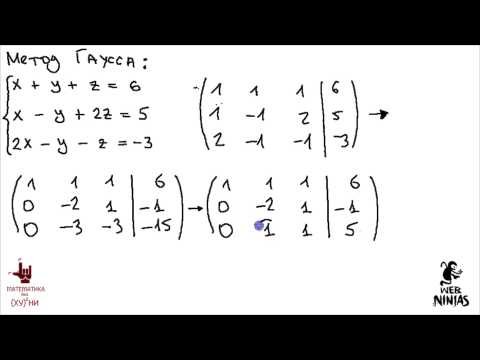
Математика без Ху%!ни. Метод Гаусса.


Для системы из двух уравнений с двумя переменными можно использовать графический метод для наглядного представления решения.
