Основные методы вычисления линейного угла двугранного угла в треугольной пирамиде
Линейный угол двугранного угла в треугольной пирамиде — это важный элемент геометрических расчетов, который играет ключевую роль в определении пространственных отношений между гранями. Понимание его вычисления поможет лучше ориентироваться в сложных задачах, связанных с многогранниками и геометрией. В этой статье представлены полезные советы, которые помогут вам правильно и точно вычислять линейный угол для различных геометрических фигур, а также рекомендации по эффективному решению задач с треугольной пирамидой.
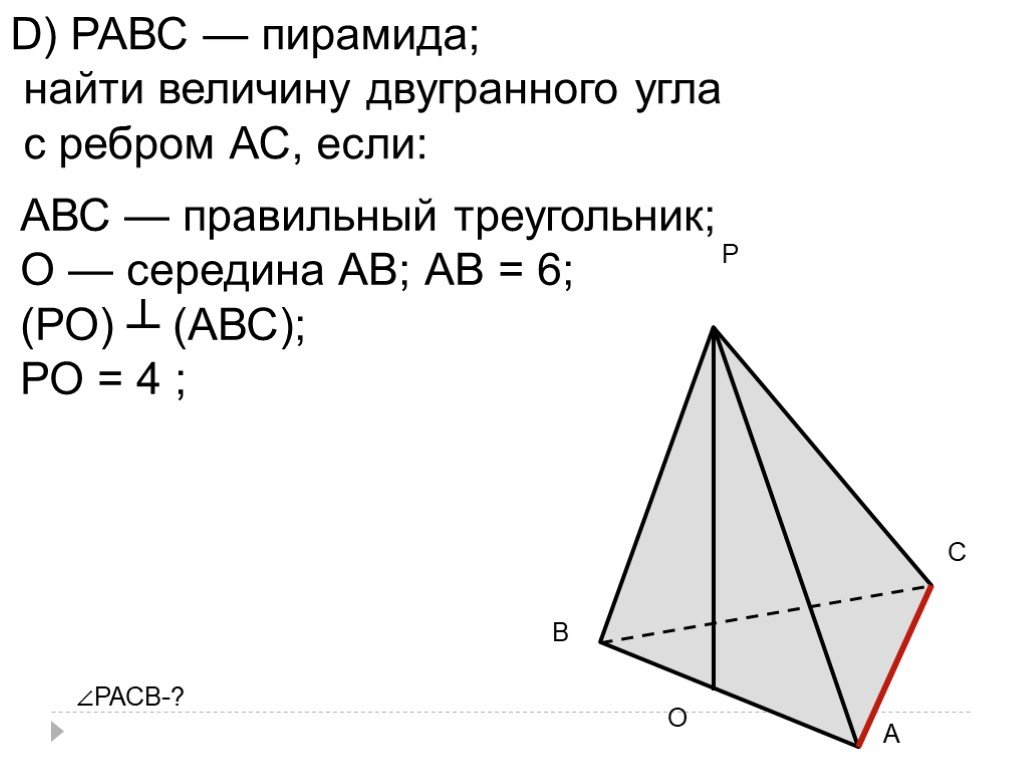

Для вычисления линейного угла двугранного угла треугольной пирамиды используйте формулу, основанную на скалярном произведении нормальных векторов.

Трехгранный угол в пирамиде
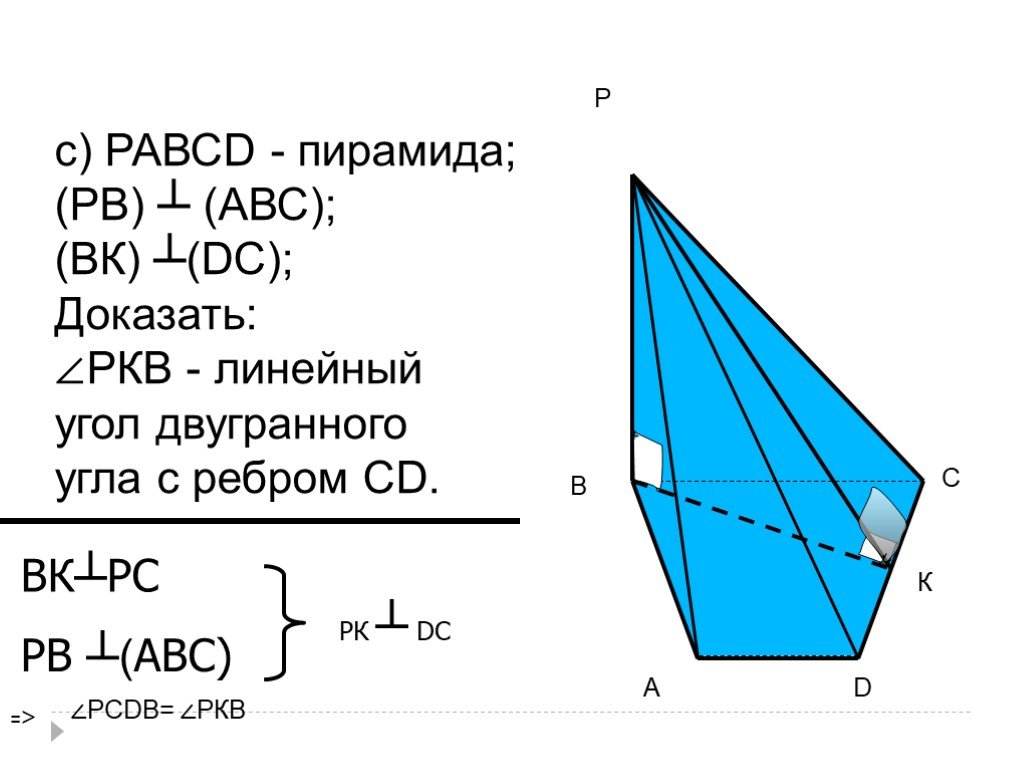
При решении задач важно правильно определить нормали к граням пирамиды, поскольку они играют ключевую роль в вычислениях углов.

ДВУГРАННЫЕ УГЛЫ ЧАСТЬ I #shorts #егэ #огэ #математика #профильныйегэ
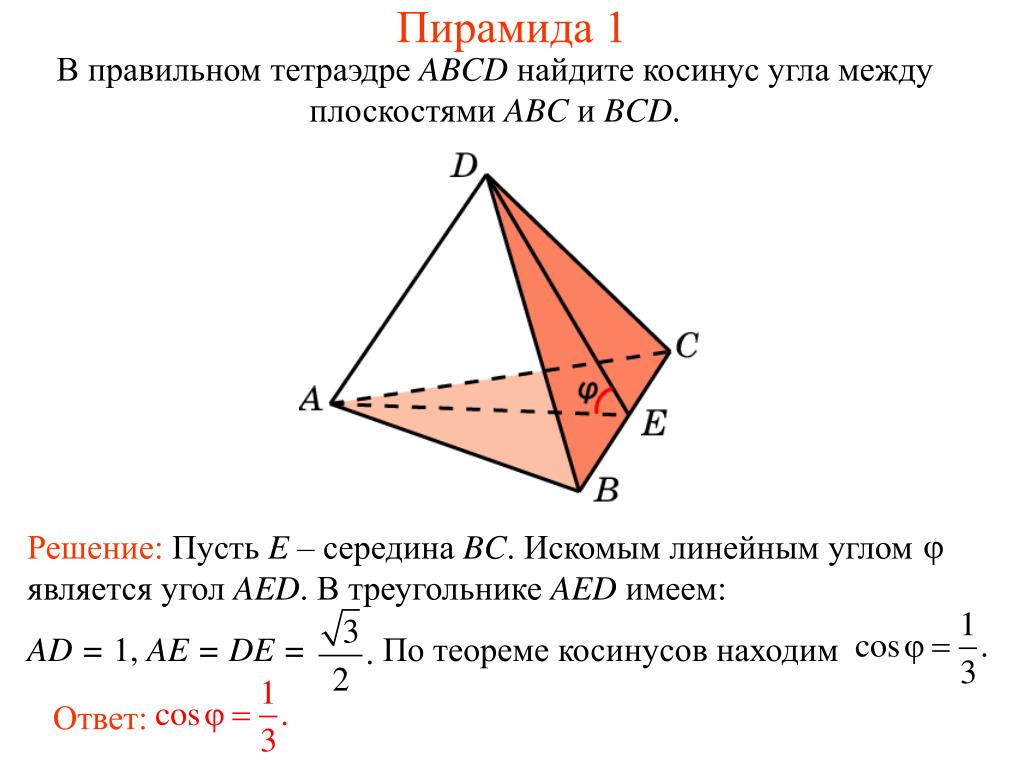
Обратите внимание на то, что линейный угол всегда измеряется между двумя плоскостями, которые образуют двугранный угол.

2. Измерение горизонтальных углов оптическим теодолитом 4Т30 способом приемов
Использование векторной алгебры значительно облегчает расчет линейного угла, особенно при сложных конфигурациях многогранников.

Угол между прямыми, плоскостями, прямой и плоскостью - Математика ЕГЭ для 10 класса - Умскул
Для более точных вычислений рекомендуется использовать координаты вершин пирамиды для определения уравнений ее граней.
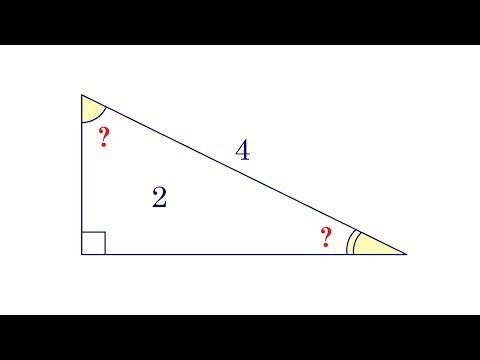
Только 1% может решить эту хитрую задачу ★ Найдите углы треугольника ★ Супер ЖЕСТЬ
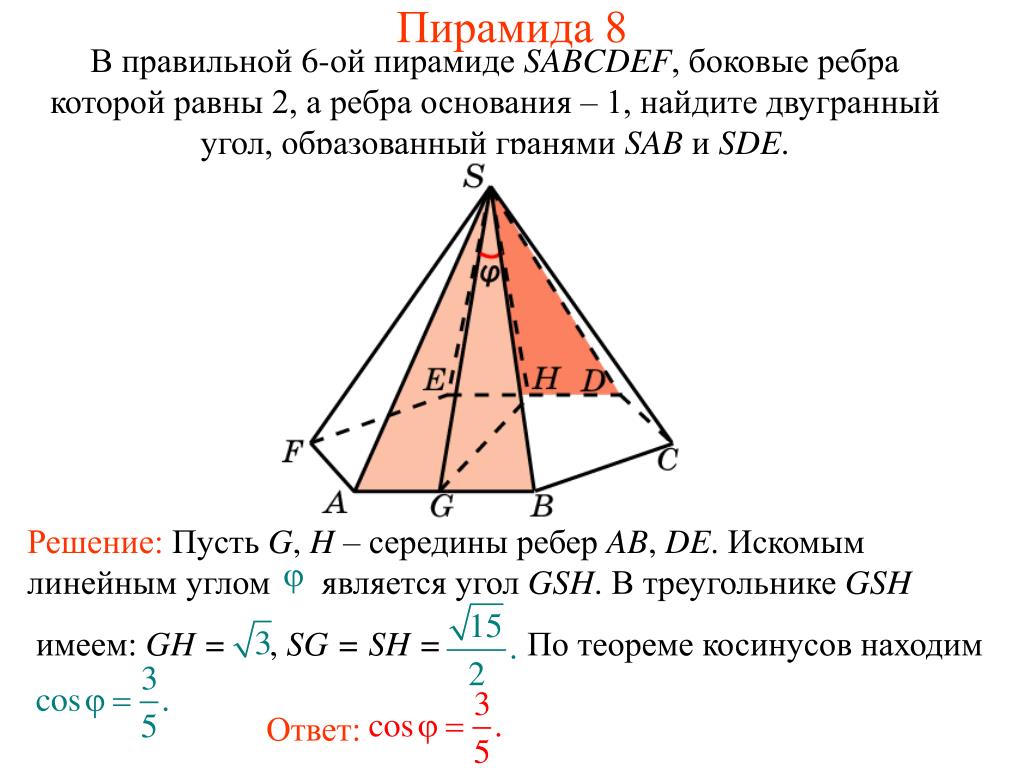
Не забывайте, что угол между плоскостями всегда находится в пределах от 0 до 90 градусов, что важно учитывать при интерпретации результата.

№257. Высота правильной треугольной пирамиды равна h, а двугранный угол при стороне основания
Понимание взаиморасположения граней треугольной пирамиды поможет избежать ошибок при вычислениях линейных углов.

10 класс, 22 урок, Двугранный угол
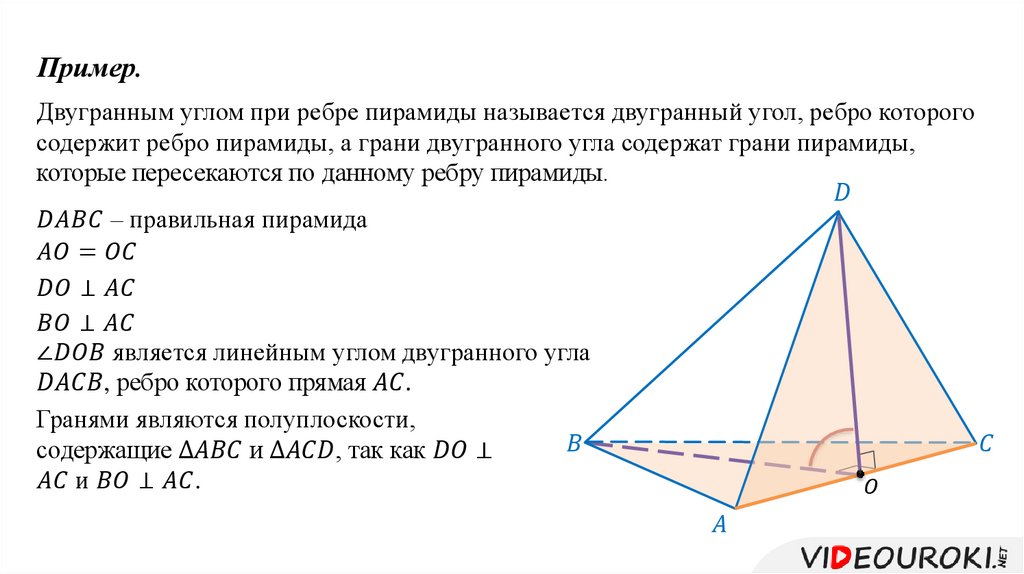
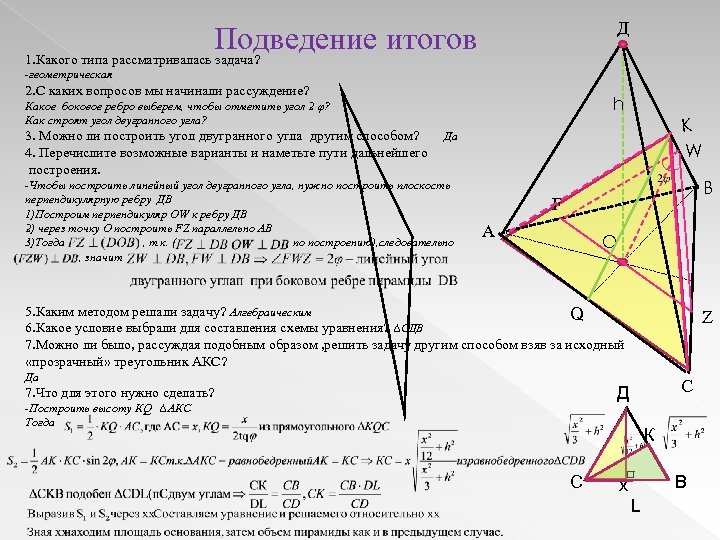
Для сложных примеров с несколькими углами полезно использовать методы проектирования, чтобы упростить расчет двугранных углов.
При работе с пирамидой можно также воспользоваться симметрией, чтобы найти общий подход к вычислениям для разных случаев.
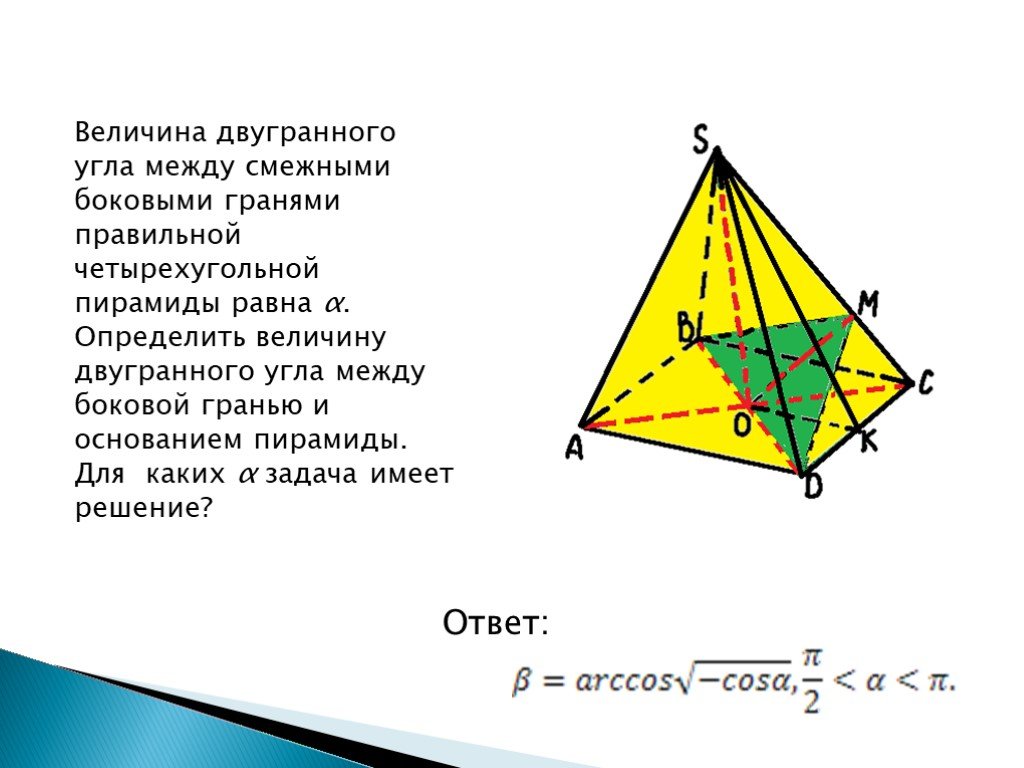
Не забывайте проверять единицы измерения и корректность вычислений, особенно если используете программное обеспечение для выполнения расчетов.

