Основные формулы для нахождения координат и длины вектора: советы по решению задач
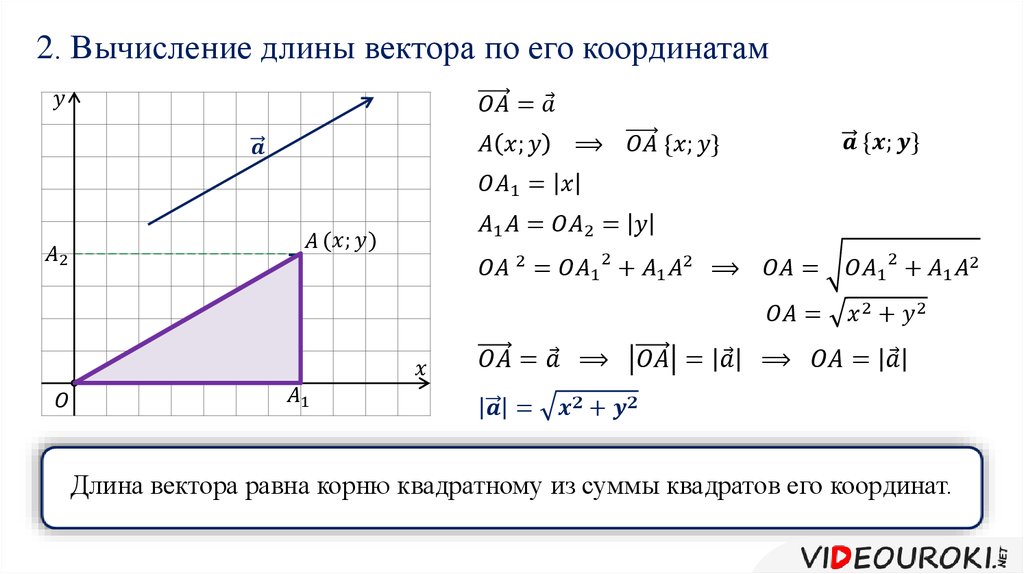
Вектор — это математический объект, который имеет как величину, так и направление. В этой статье мы рассмотрим, как вычислить координаты вектора, определить его длину, а также познакомим вас с ключевыми формулами и практическими рекомендациями для успешного решения задач по этой теме.
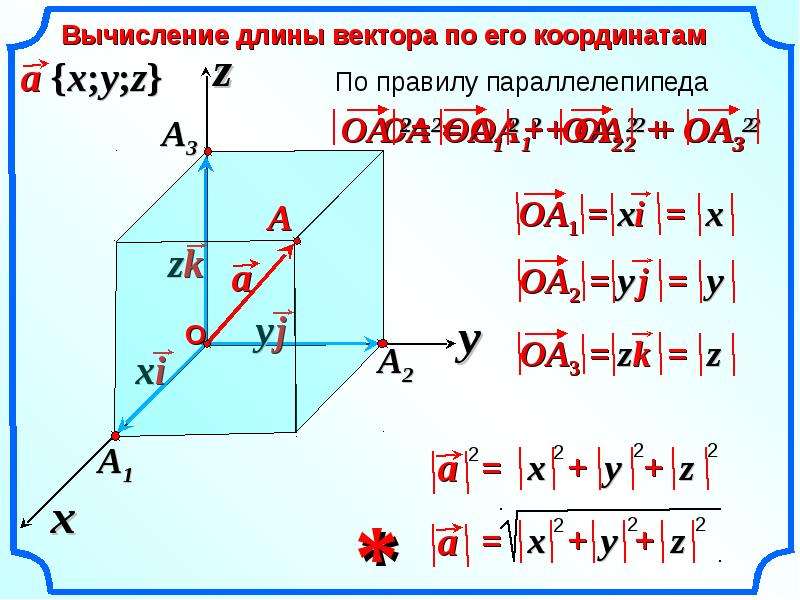

Для нахождения длины вектора используйте формулу: |v| = √(x² + y² + z²), где x, y и z — компоненты вектора.

Все о векторах за 60 минут - Математика ОГЭ - Молодой Репетитор


Если вектор задан координатами двух точек A(x₁, y₁, z₁) и B(x₂, y₂, z₂), длина вектора AB рассчитывается по формуле: |AB| = √((x₂ - x₁)² + (y₂ - y₁)² + (z₂ - z₁)²).

Координаты вектора. 9 класс. п.6 - основные формулы нахождения координат вектора, его длины.

Для вычисления направления вектора важно помнить, что его компоненты пропорциональны разнице соответствующих координат начальной и конечной точек.

Скалярное произведение векторов


Запомните, что вектор, длина которого равна нулю, называется нулевым вектором и имеет неопределенное направление.

Консультация к коллоквиуму по квантовой физике, Глазков В.Н., 07.12.2024

При вычислениях длины вектора в трехмерном пространстве используйте формулу для расстояния между двумя точками в пространстве, включающую все три координаты.

Длина вектора через координаты. 9 класс.


Не забывайте о важности правильной постановки задачи, особенно при вычислениях вектора на плоскости или в пространстве.

Координаты вектора. Длина вектора


Убедитесь, что используете правильные единицы измерения для всех координат вектора, чтобы результат был корректным.

Координаты вектора. Длина вектора. Геометрия 9

Если вектор задан векторными компонентами, то его длину можно также найти как корень из суммы квадратов всех его компонент.

Векторы за 45 минут с НУЛЯ до ЕГЭ

Координаты вектора. 9 класс.


Не путайте вектор с направленным отрезком, даже если они визуально схожи, так как вектор определяется только своим направлением и длиной, а не конкретными точками.
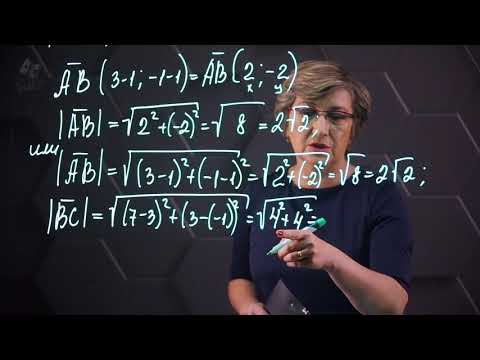
Нахождение длины вектора через координаты. Практическая часть. 9 класс.


Для более сложных задач, включающих работу с углами между векторами, используйте формулу скалярного произведения для вычисления угла между ними: cos(θ) = (A·B) / (|A| * |B|).