Определение координат середины отрезка в пространстве: простые шаги и важные детали
В данной статье мы расскажем, как правильно вычислить координаты середины отрезка в трехмерном пространстве, используя формулы и наглядные примеры. Это важная тема в геометрии и физике, которая позволяет быстро и эффективно решать задачи, связанные с нахождением средней точки отрезка. Вы узнаете, как правильно применить формулы для нахождения середины отрезка и что нужно учитывать при решении подобных задач.


Для нахождения координат середины отрезка в трехмерном пространстве, нужно просто усреднить координаты его концов.

Расстояние между двумя точками с заданными координатами. Координаты середины отрезка - 9 класс

Формула для середины отрезка выглядит как: M = ((x1 + x2)/2, (y1 + y2)/2, (z1 + z2)/2).

Формула для вычисления середины отрезка (видео 51) - Подобие. Геометрия - Математика

Не забывайте, что середина отрезка всегда лежит на прямой, соединяющей его концы.

КООРДИНАТЫ СЕРЕДИНЫ ОТРЕЗКА Атанасян 425 стереометрия

Если отрезок имеет координаты концов A(x1, y1, z1) и B(x2, y2, z2), то координаты середины M будут (x1+x2)/2, (y1+y2)/2 и (z1+z2)/2.
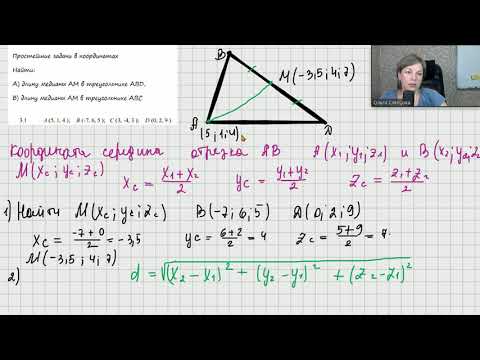
простейшие задачи в координатах координаты середины отрезка
Важно помнить, что при вычислении координат нужно учитывать все три оси: X, Y и Z.
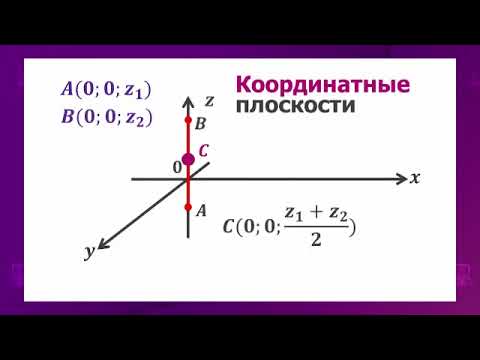
Геометрия 10 класс Координаты середины отрезка в пространстве 09 03 2021

Для практики можно использовать различные примеры, чтобы убедиться в правильности расчетов.

Самый короткий тест на интеллект Задача Массачусетского профессора

Геометрически можно представить середину отрезка как точку, которая делит его пополам.

Координаты вектора. 9 класс.

Чтобы избежать ошибок, всегда проверяйте правильность выполнения операций при нахождении средней точки.

Координаты середины отрезка. Формула. Геометрия 9 класс.

Координаты середины отрезка


Если отрезок параллелен одной из осей, то координаты середины будут зависеть только от координат, соответствующих этим осям.

Используйте визуализацию на графике, чтобы лучше понять принцип нахождения середины отрезка.
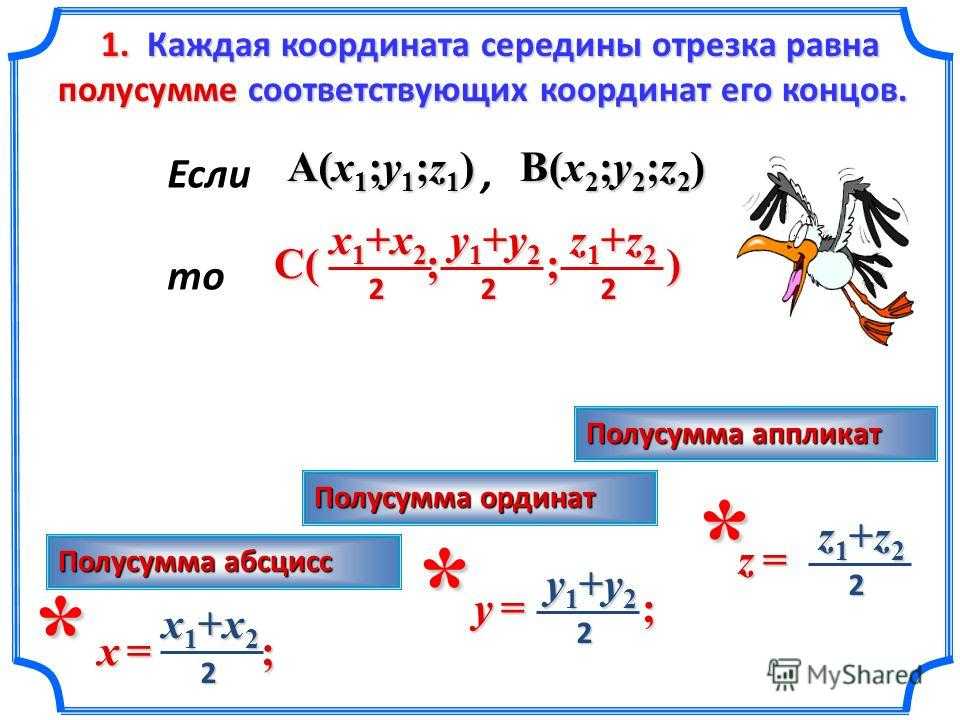

Координаты середины отрезка. Практическая часть. 11 класс.