Определение количества решений уравнения f(x) = 0 через графическое представление первообразной функции
На этой странице вы найдете полезную информацию о том, как определить количество решений уравнения f(x) = 0, исследуя график его первообразной функции. Это важно для анализа поведения функции и нахождения точек пересечения с осью абсцисс. Рассмотрим несколько советов, которые помогут вам быстро и правильно определить такие решения.
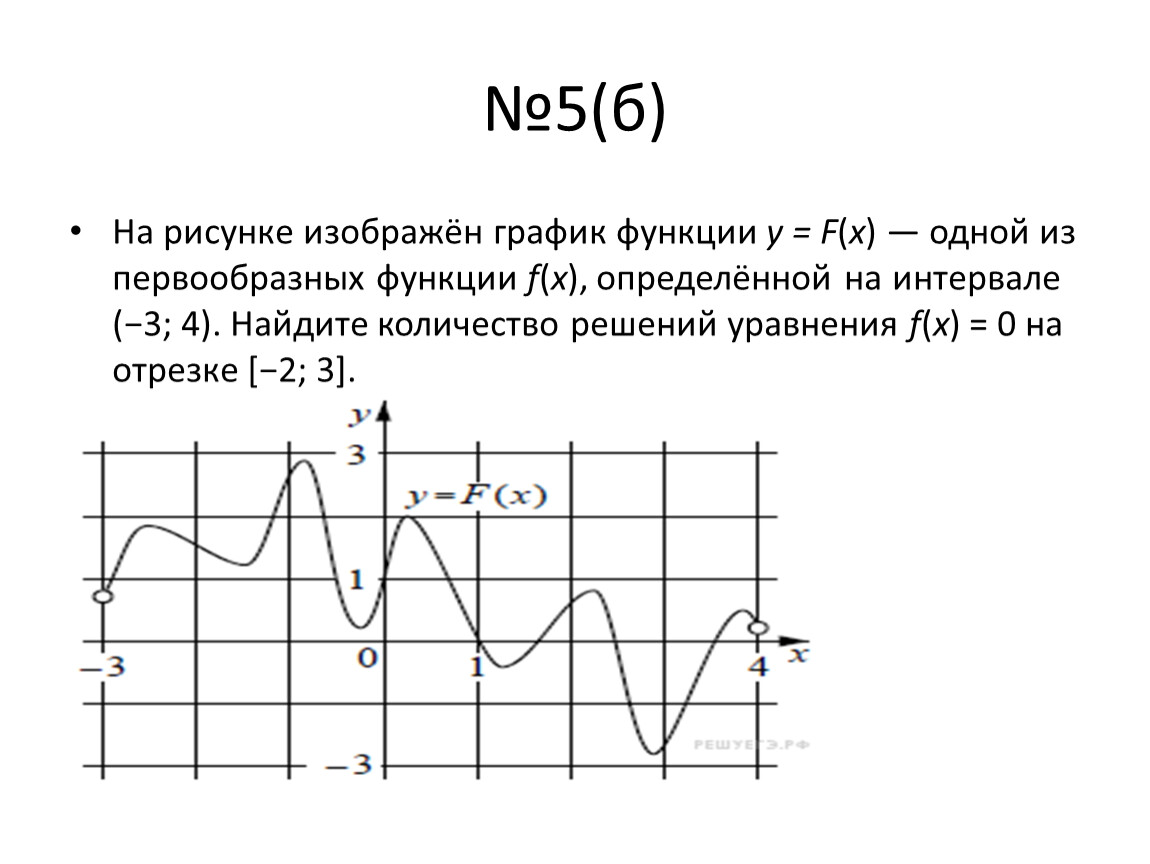
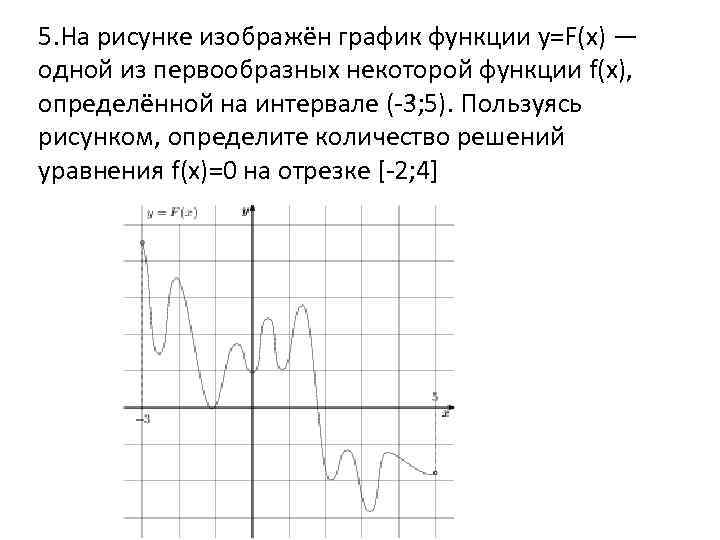
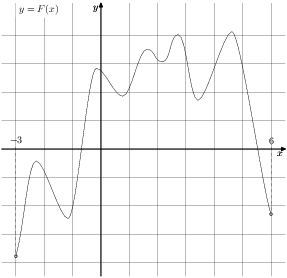
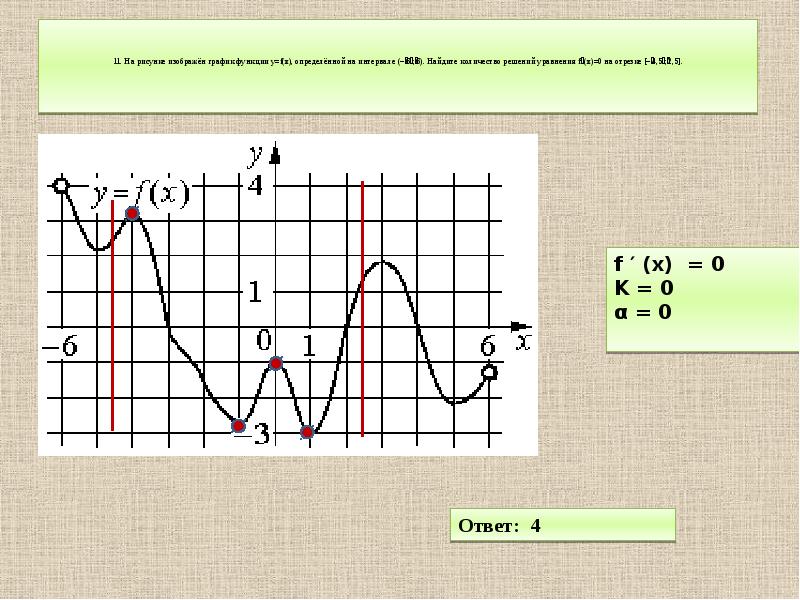
Для нахождения количества решений уравнения f(x) = 0 по графику первообразной функции, ищите количество точек пересечения графика с осью абсцисс.
Задание В8

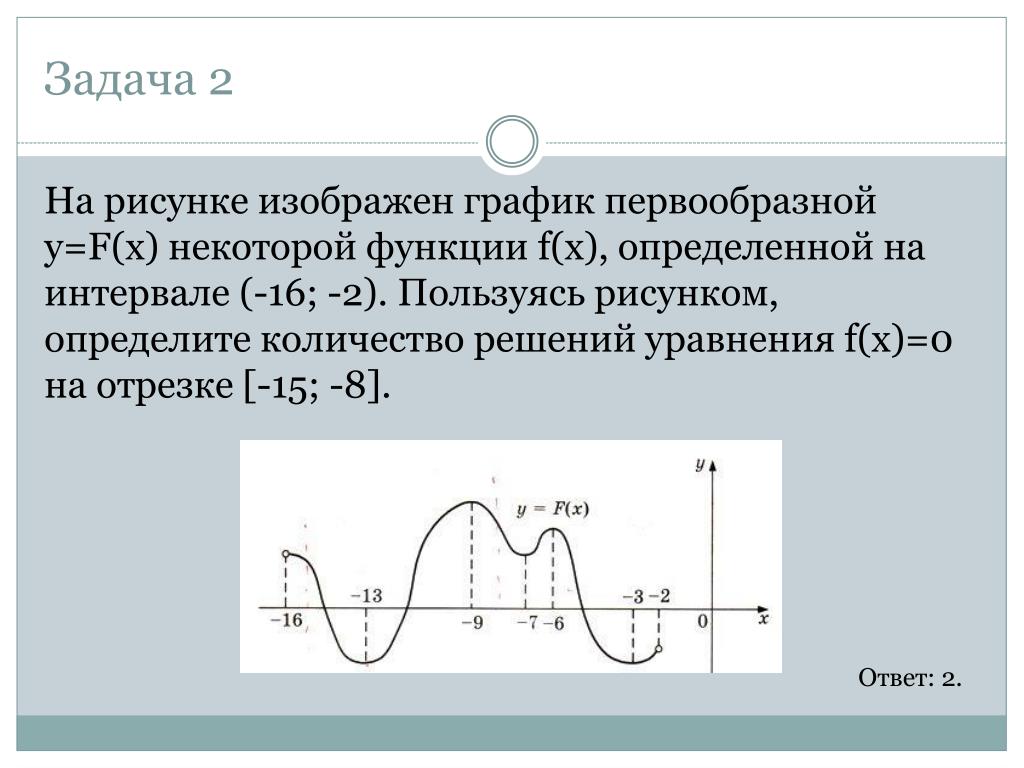
Каждая точка пересечения графика первообразной функции с осью X соответствует возможному решению уравнения f(x) = 0.
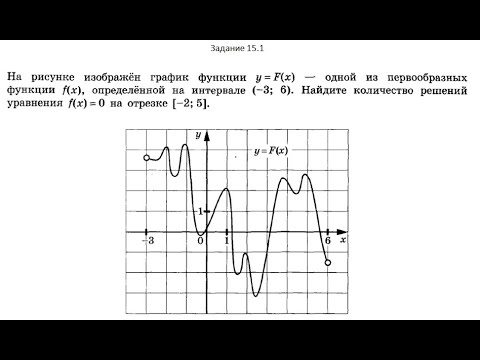
Производные, номер 15.1, ЕГЭ по профильной математике

Если график первообразной функции не пересекает ось X, это может означать, что у уравнения нет решений в данной области.
Первообразная. 11 класс.
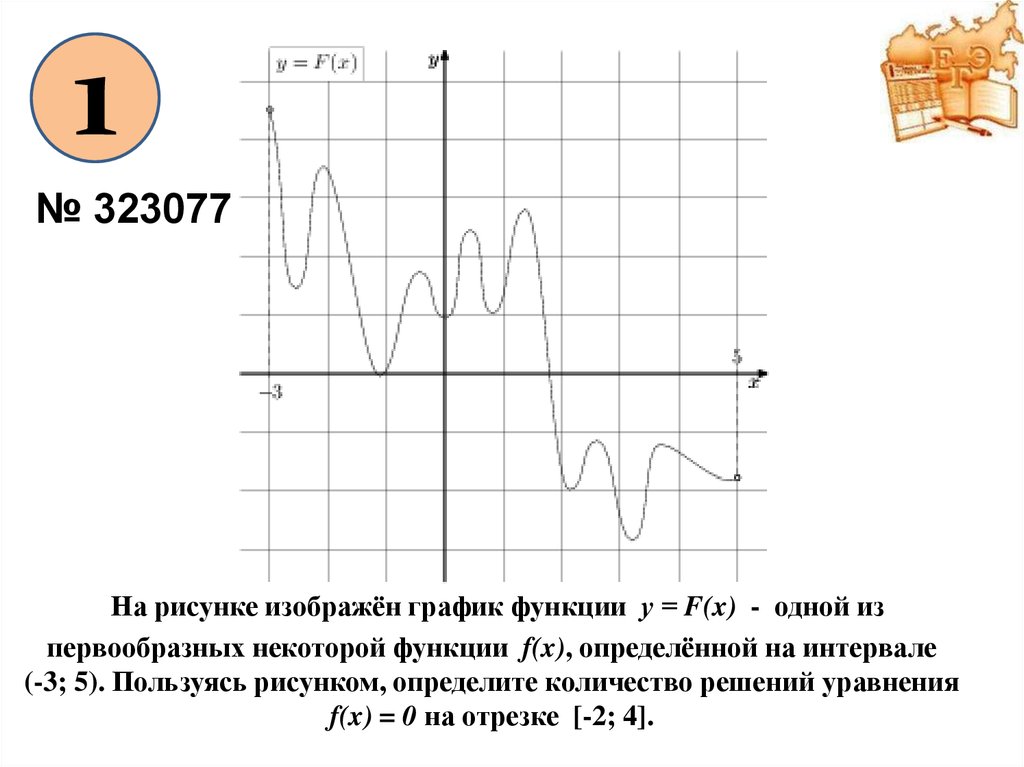
Если график функции имеет несколько пересечений с осью X, то у уравнения может быть несколько решений.

ЭКЗАМЕН ПО МАТАНУ ИЗ МФТИ - ГРОБ ИЛИ ХАЛЯВА???


График первообразной функции помогает наглядно понять поведение функции f(x) и увидеть, где она равна нулю.
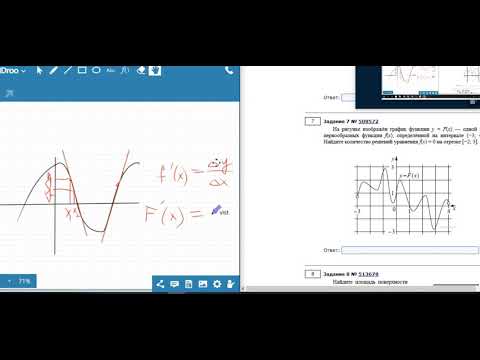
Найдите количество решений уравнения fx = 0 Д160
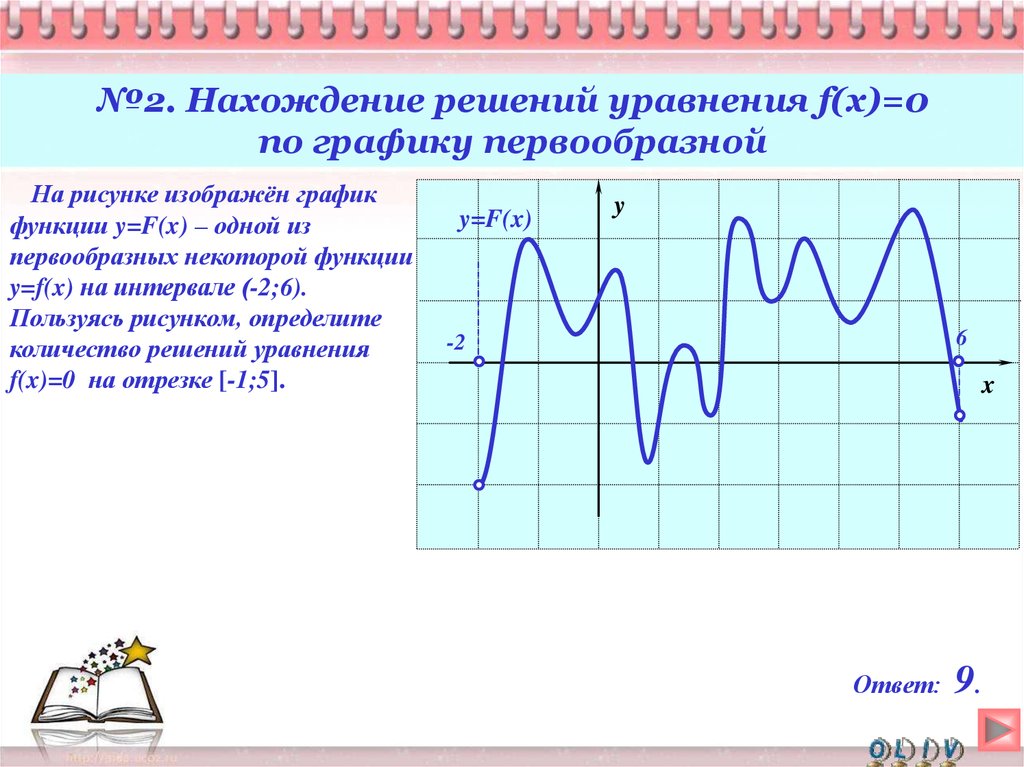
Чтобы точнее определить количество решений, уточните, где именно график функции пересекает ось абсцисс (можно использовать числовые методы или графические калькуляторы).
8.12.2022 Первообразная - 7 задание ЕГЭ Урок 4
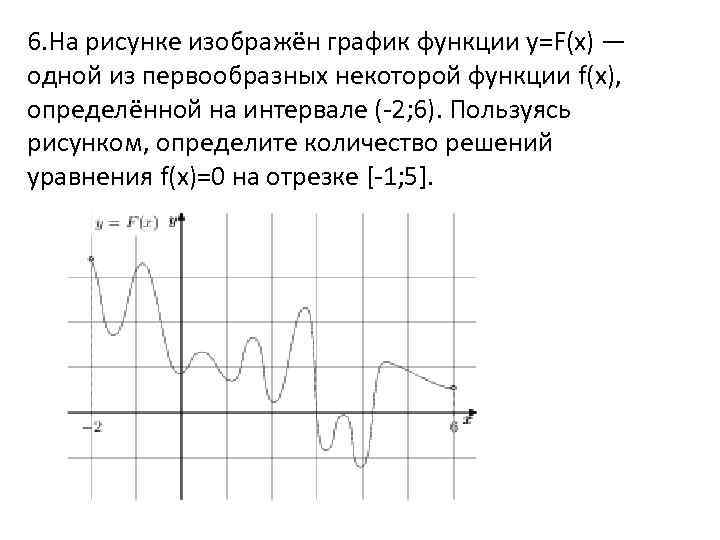
Если график функции непрерывен и плавно пересекает ось X, это может указывать на единственное решение уравнения.
ПЕРВООБРАЗНАЯ функции / разбор задания #323077 / ПРОФИЛЬ

В случае разрывов графика первообразной функции, решение может быть единственным в каждом из промежутков, где функция непрерывна.

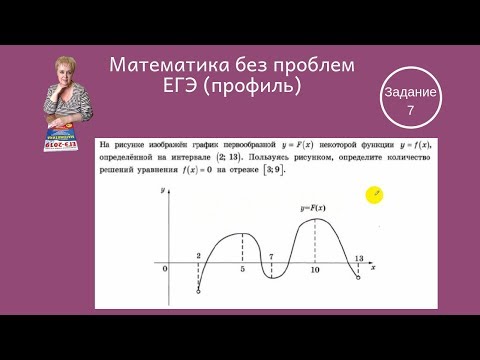
На рисунке изображён график функции 𝑦=𝐹(𝑥)— одной из первообразных некоторой функции 𝑓(𝑥)

Для сложных функций, которые могут иметь несколько экстремумов, внимательно анализируйте, как график меняет направление, что может подсказать возможные решения.
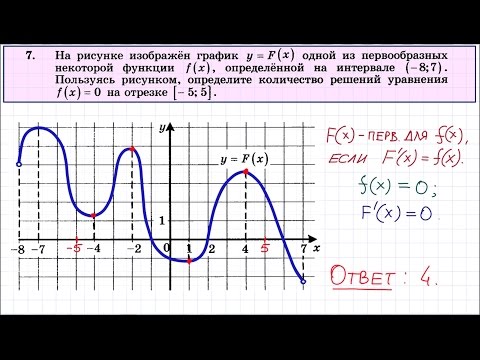
Задание 7 ЕГЭ по математике
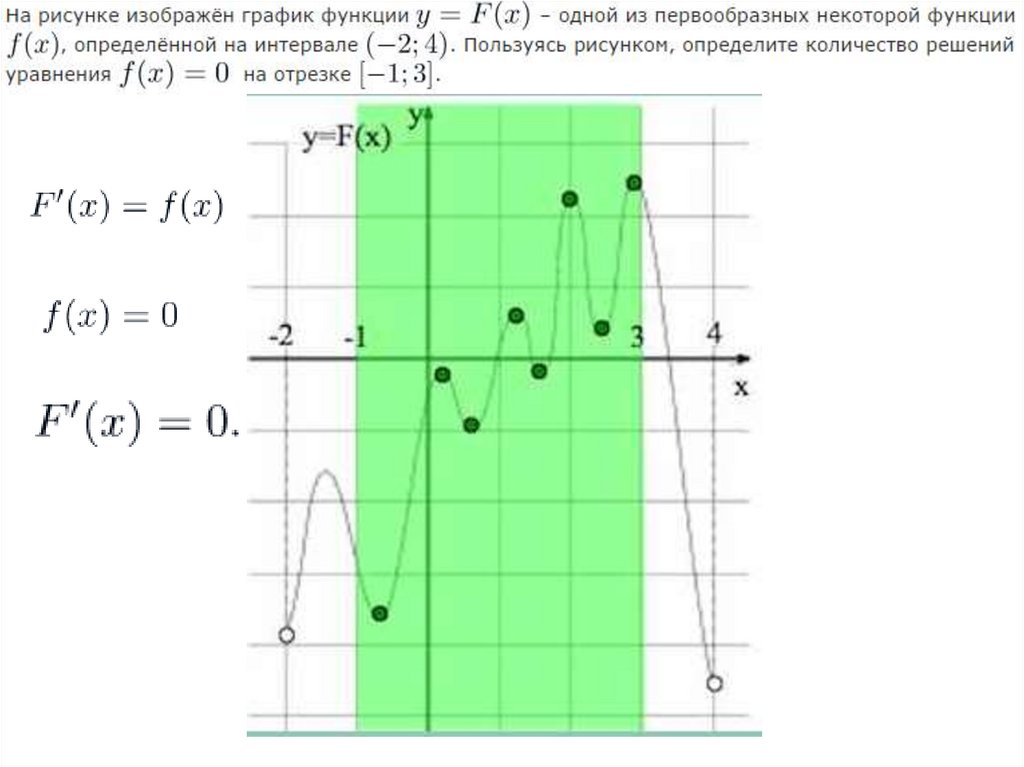
Использование производной функции и её графика помогает дополнительно понять, как изменения функции влияют на количество решений уравнения f(x) = 0.
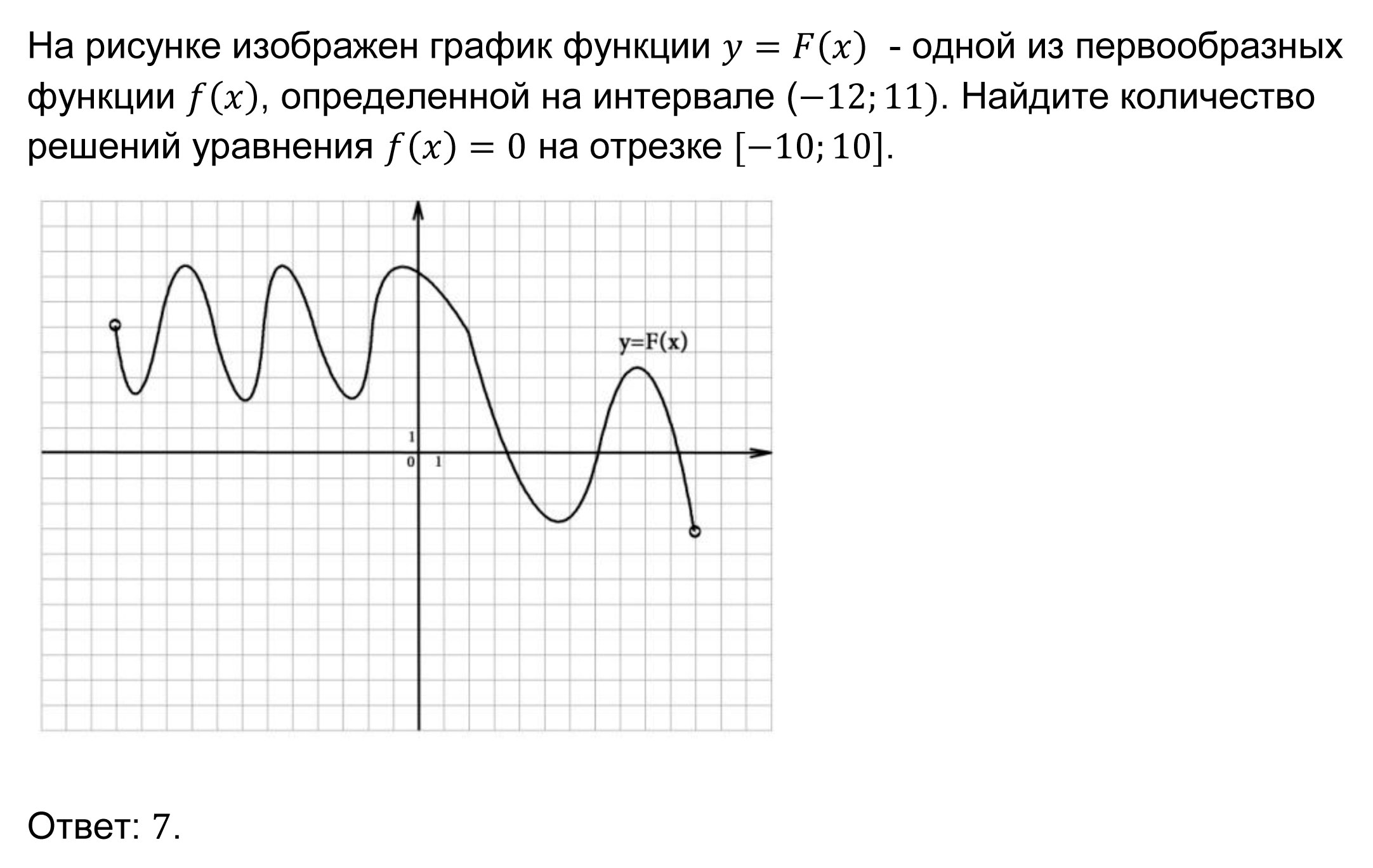
Как по графику первообразной определить количество корней уравнения y=fx