Фигуры с углом в 60 градусов: что стоит о них знать?
На данной странице мы рассматриваем фигуры, которые могут содержать угол 60 градусов. Мы объясним, какие геометрические объекты могут быть описаны этим углом и как они выглядят. Это полезная информация для всех, кто изучает геометрию и интересуется свойствами различных форм.
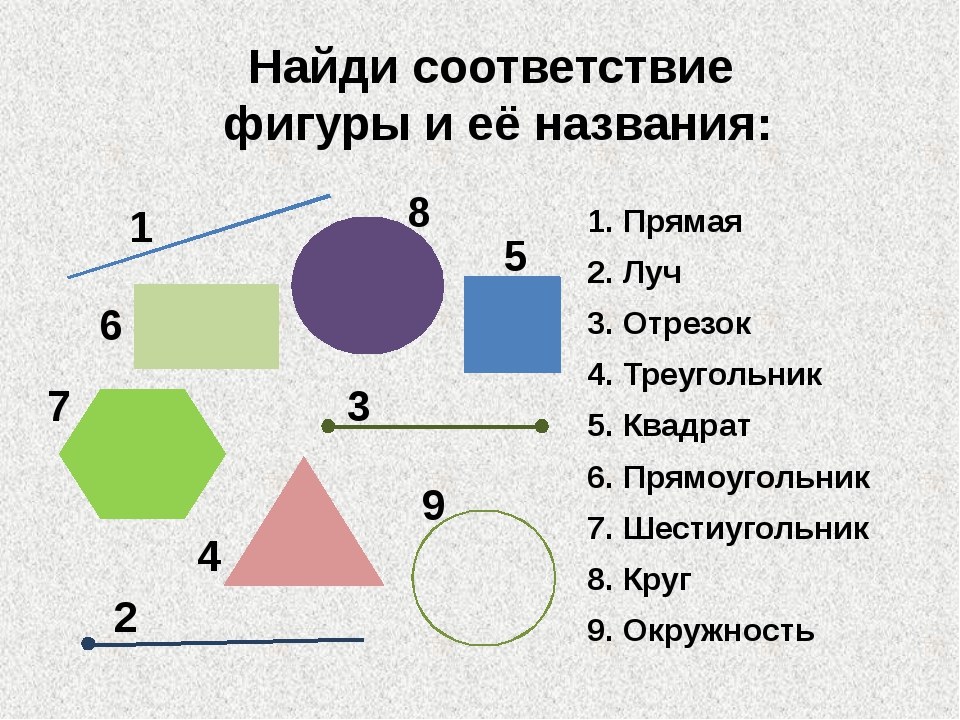
Для того чтобы понять, какие фигуры имеют угол в 60 градусов, важно обратить внимание на равносторонние треугольники.

Чудеса природы, которые действительно существуют. Самые красивые места Земли!
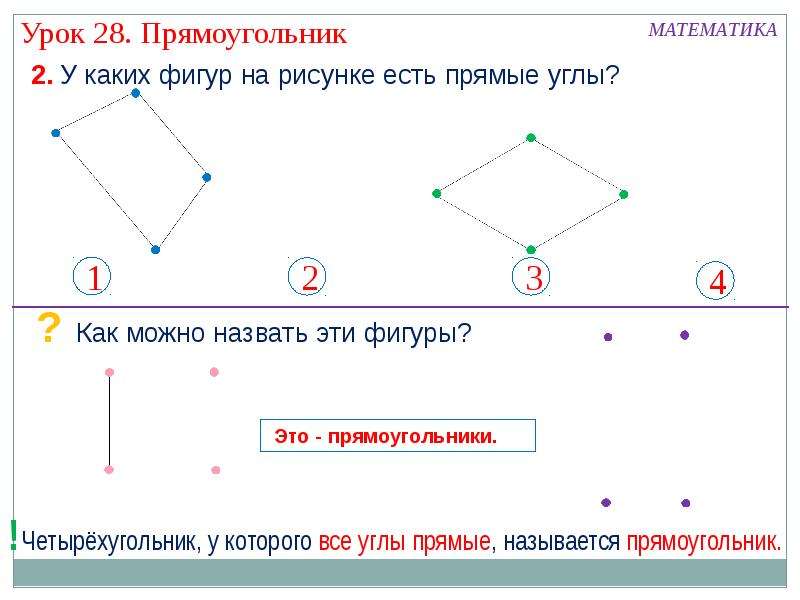
Помимо равносторонних треугольников, угол 60 градусов встречается в шестиугольниках, так как внутренние углы правильного шестиугольника равны 120 градусов, а угол между сторонами — 60 градусов.
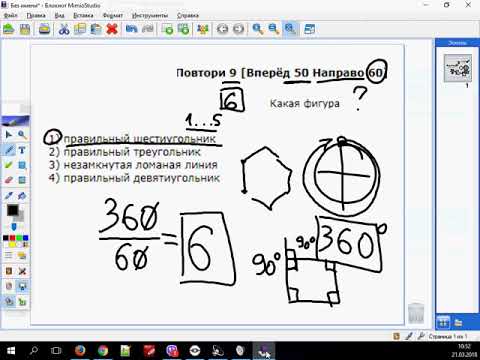
ОГЭ Информатика задание 6 Исполнитель черепашка Геометрическая фигура
Изучая фигуры с углом 60 градусов, можно заметить, что это ключевое значение в теории симметрии и регулярных многоугольников.

Какая фигура является идеальной?
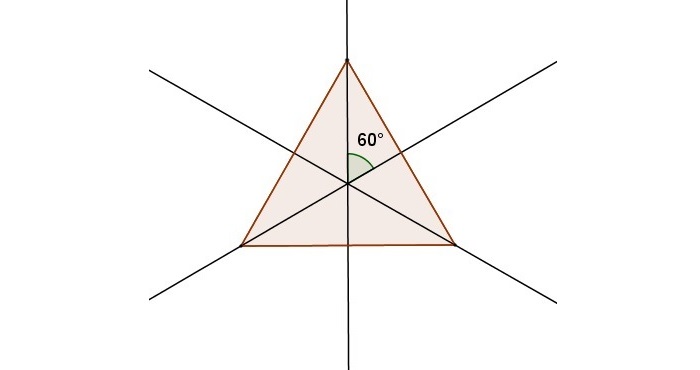

При рассмотрении углов в других фигурах, например, в правильных многоугольниках, важно помнить, что углы между соседними сторонами могут быть кратны 60 градусам.

✏️📐 Как построить угол в 60 градусов? Геометрия в действии! 😎
Помимо прямых углов, равных 90 градусам, угол 60 градусов — это один из самых распространенных углов в практике черчения и проектирования.
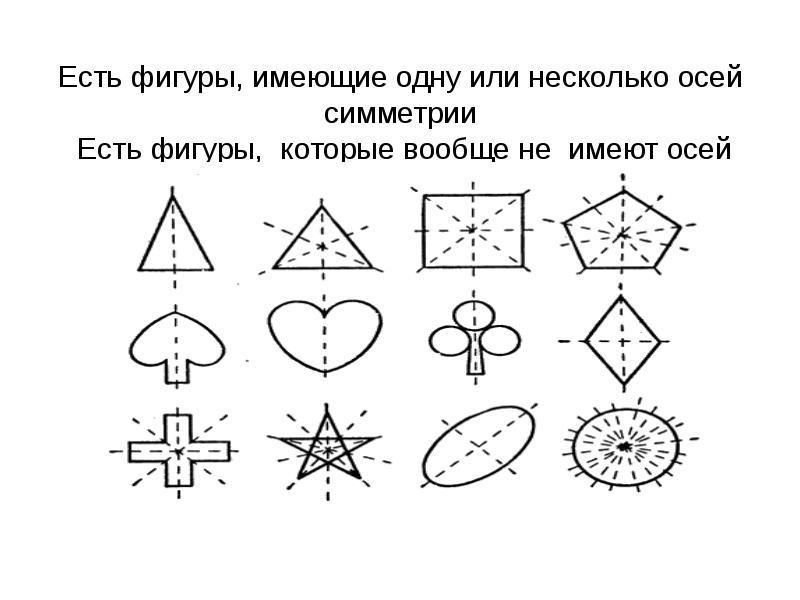
30-40. Осевая симметрия и поворот на 60 градусов
Шестиугольники и правильные треугольники являются основой для создания многих фигур, часто встречающихся в природе и архитектуре.

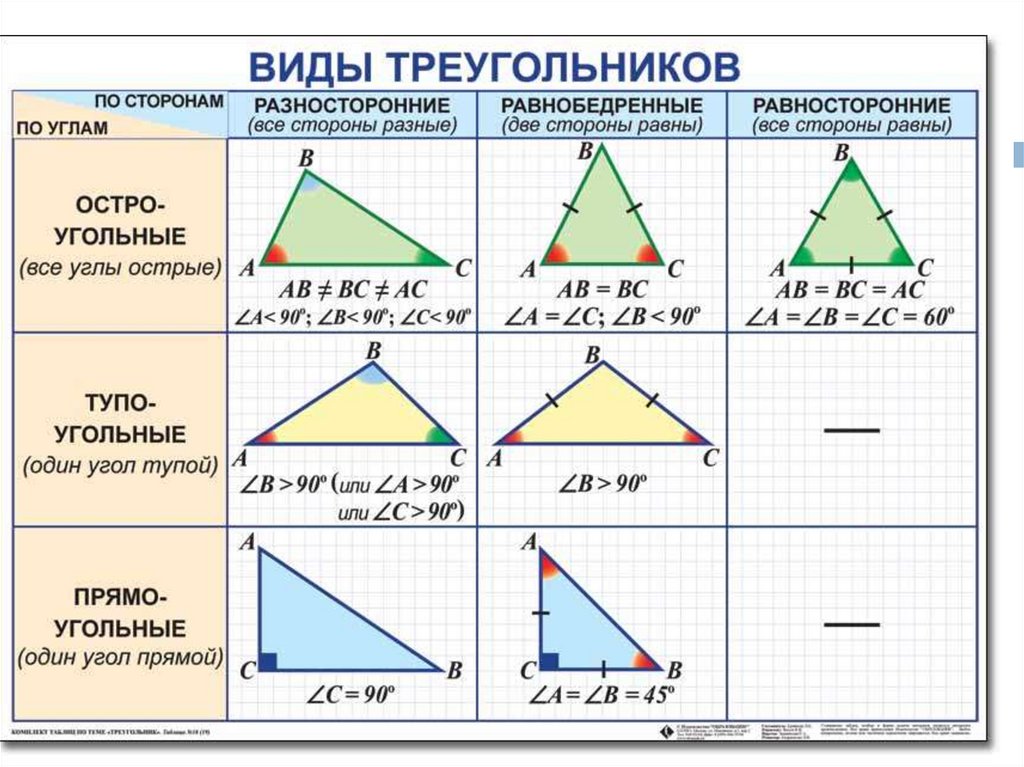
Для расчета углов в многоугольниках важно помнить, что сумма углов внутри правильного многоугольника всегда равна (n - 2) * 180 градусов, где n — количество сторон.
Если в задаче на нахождение углов вам нужно использовать 60 градусов, проверьте, являются ли ваши фигуры правильными, так как они часто обладают такими углами.
Что такое угол? Виды углов: прямой, острый, тупой, развернутый угол
Угол 60 градусов имеет прямое отношение к равносторонним треугольникам, где каждый угол равен именно этому значению.

Синус 60 градусов
Знание угла в 60 градусов поможет в решении задач на нахождение других углов в многоугольниках и при работе с регулярными многоугольниками в чертежах.
