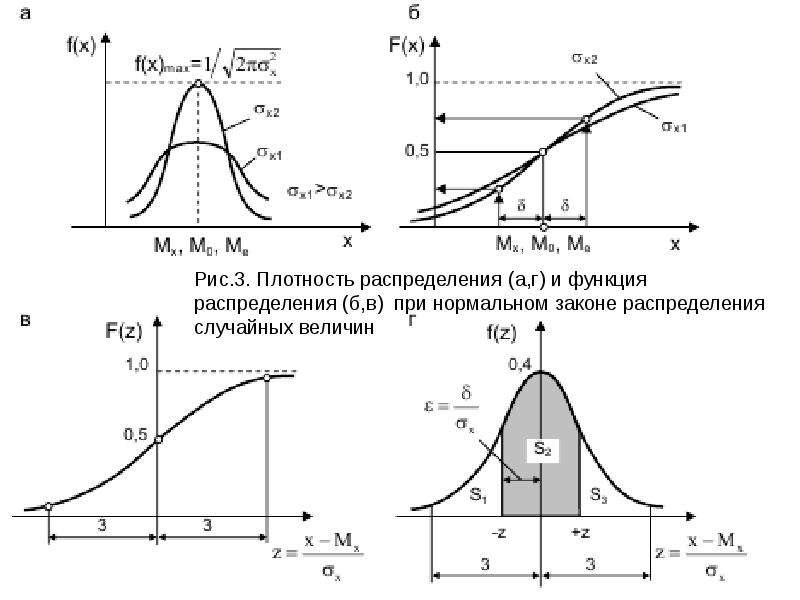
Как анализировать и использовать интегральную теоретическую кривую нормального распределения
Интегральная теоретическая кривая нормального распределения — это важный инструмент в математической статистике, который помогает анализировать и визуализировать распределение случайных величин. Она часто используется в разных областях, от финансовых исследований до психометрии. В этом разделе мы рассмотрим, как правильно интерпретировать эту кривую и как она может быть полезна в различных ситуациях.
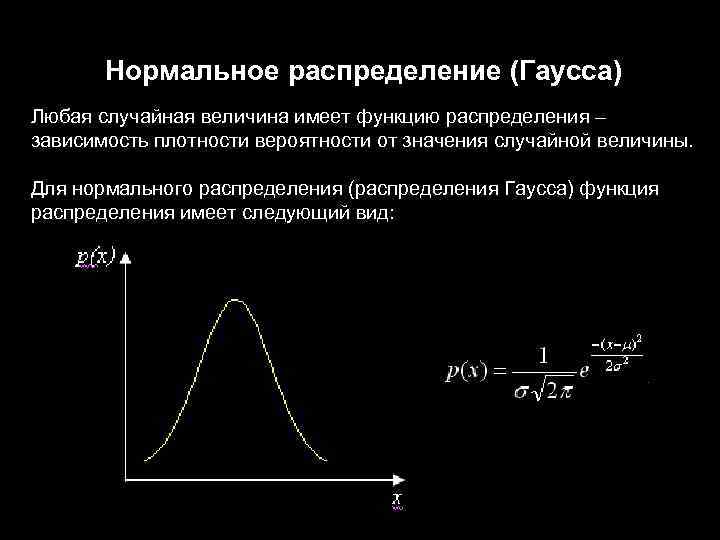
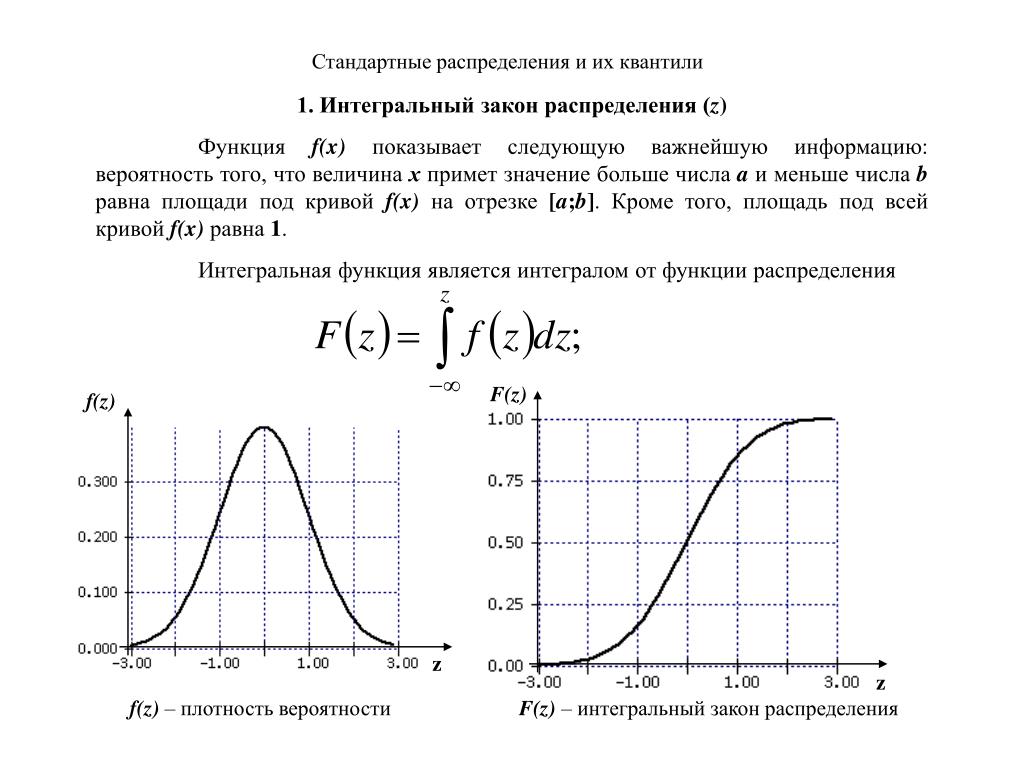
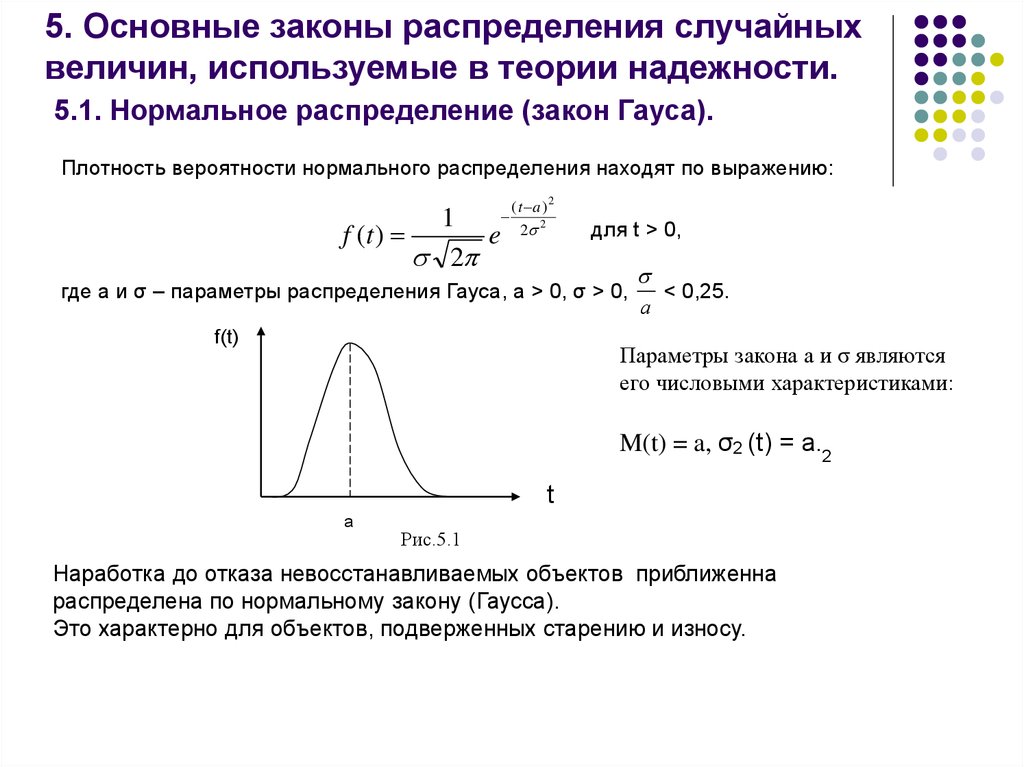
Для точного понимания кривой нормального распределения полезно изучить основные её параметры: среднее значение, стандартное отклонение и форма кривой.

11. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ 📚 Теория вероятностей
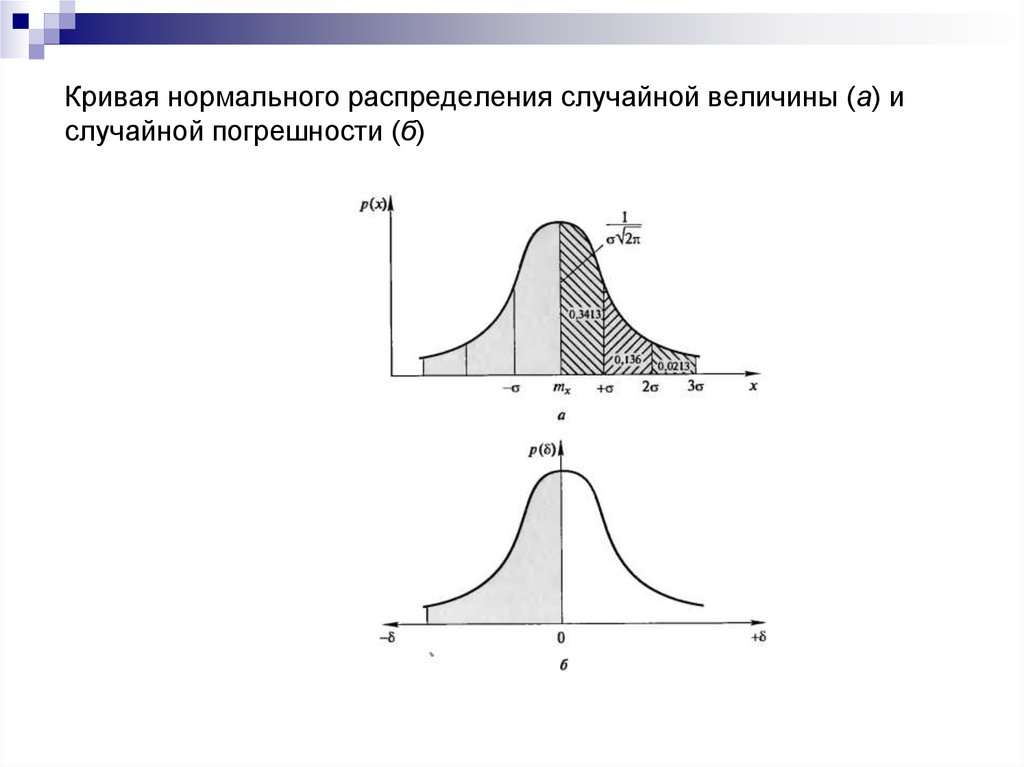
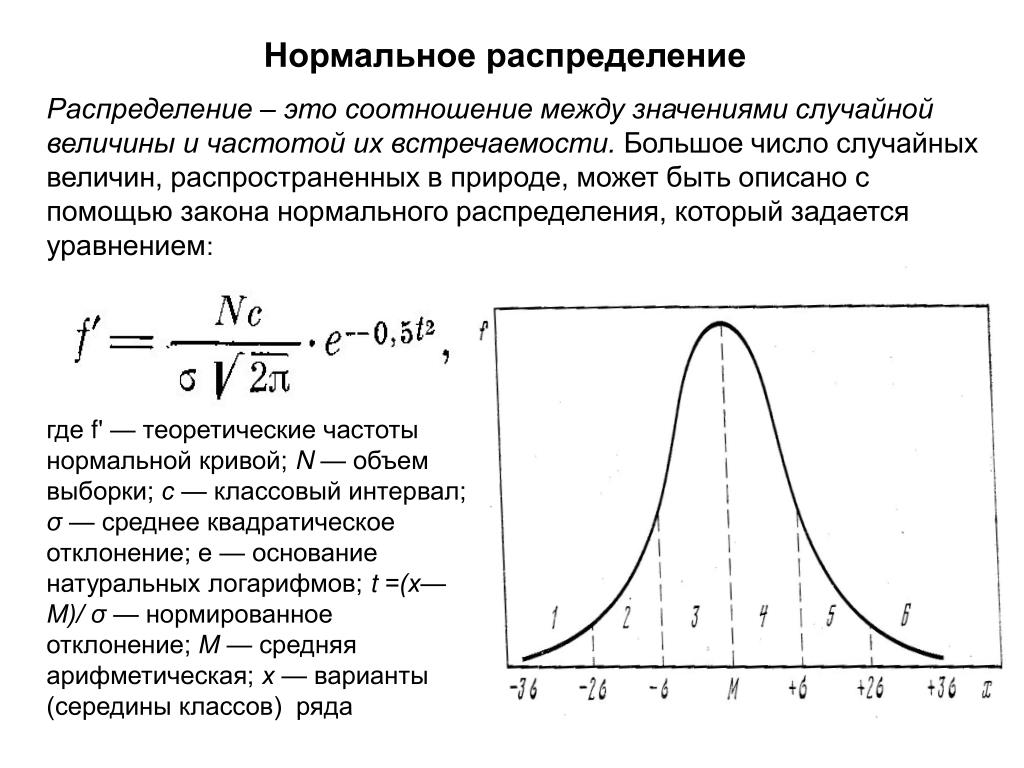
Когда вы работаете с нормальным распределением, важно помнить, что около 68% всех значений находятся в пределах одного стандартного отклонения от среднего.
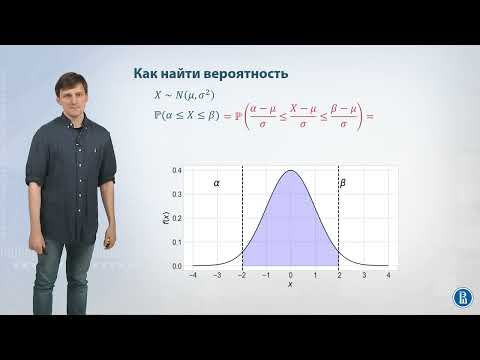
02-04 Нормальное распределение и его свойства
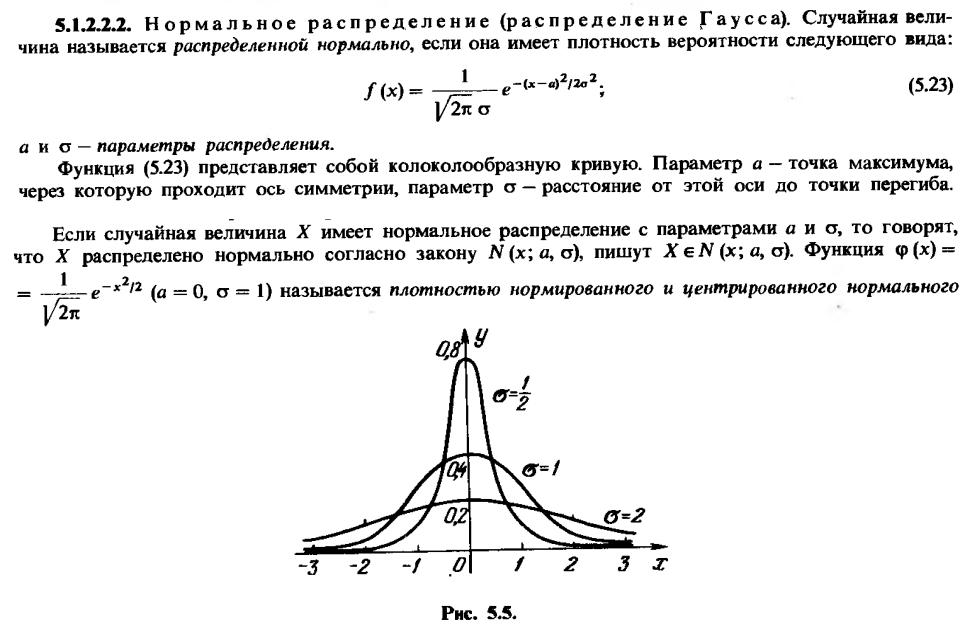
Использование интегральной кривой нормального распределения помогает визуализировать вероятность попадания случайной величины в определённый интервал.
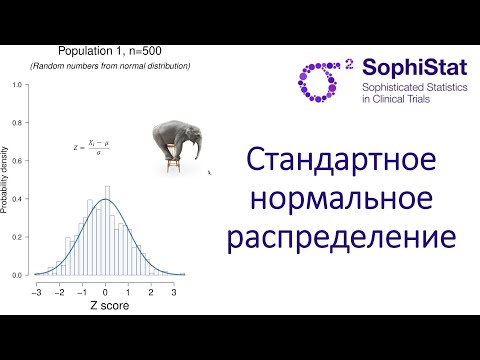
3.2 Стандартное нормальное распределение
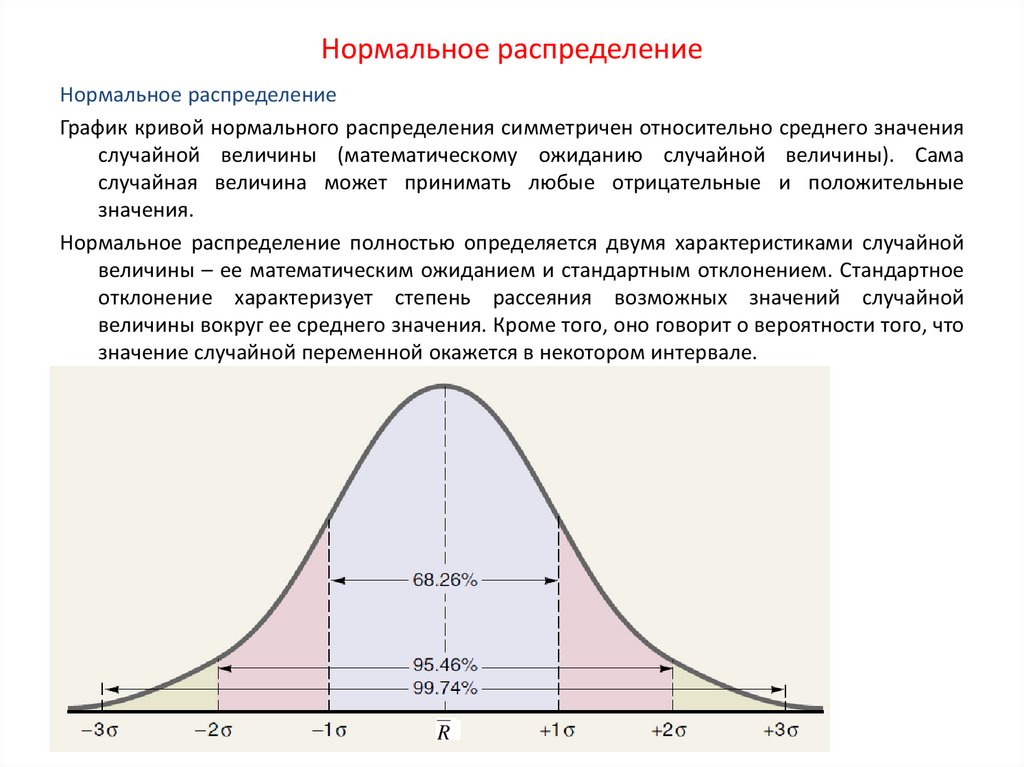
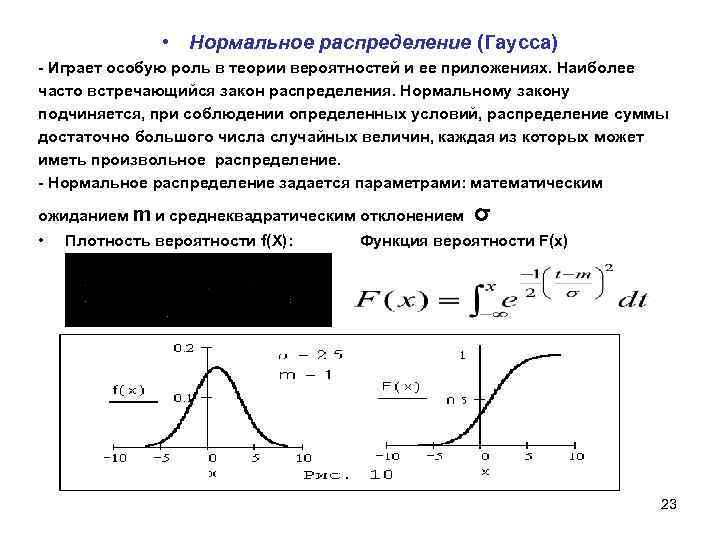
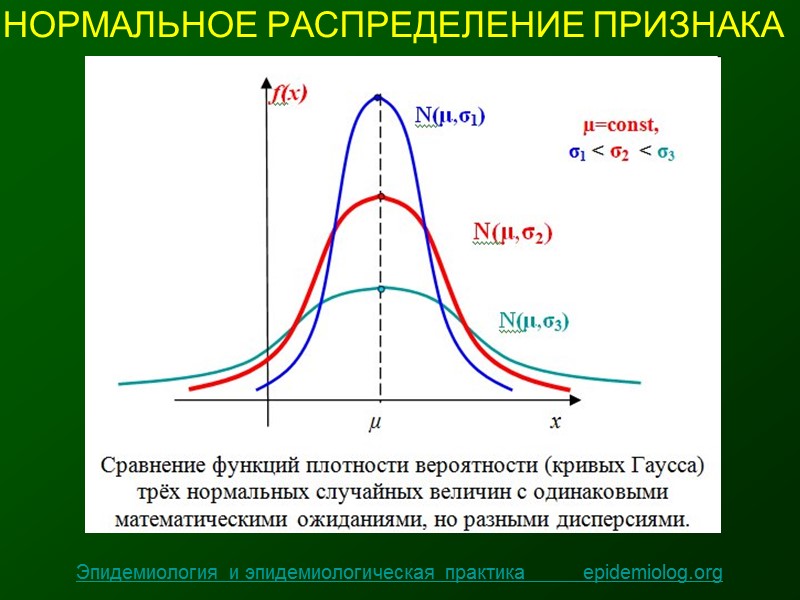
Изучая график нормального распределения, полезно обращать внимание на его симметричность относительно среднего значения, что является ключевым признаком этого распределения.

Самое нормальное распределение // Vital Math
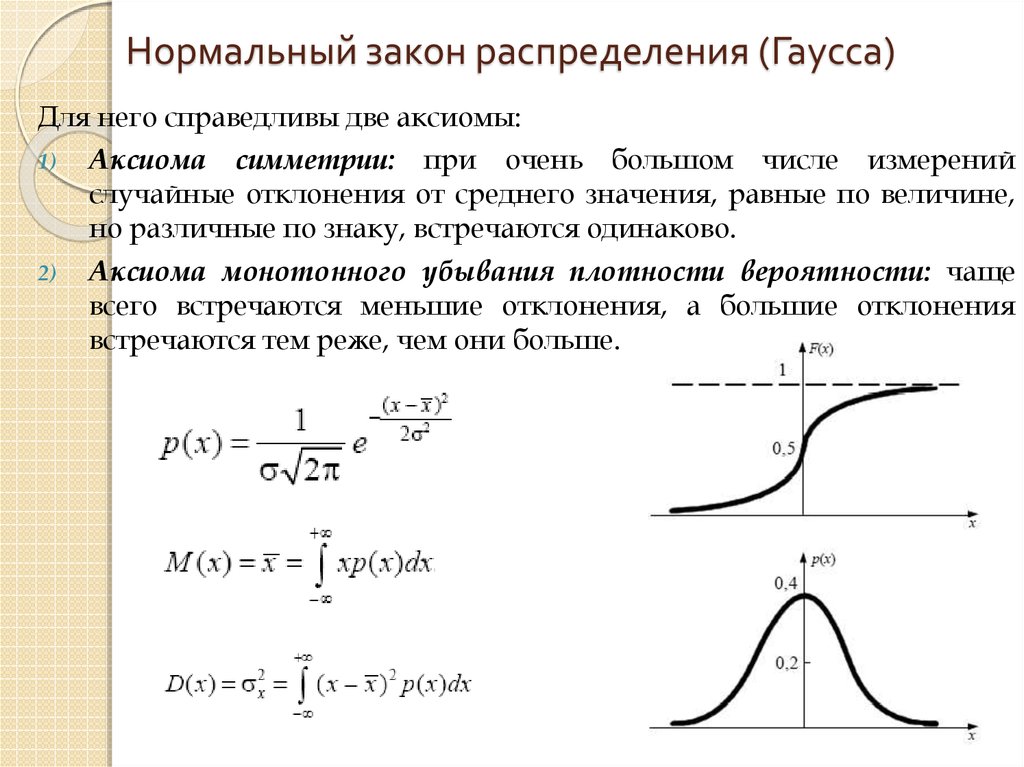
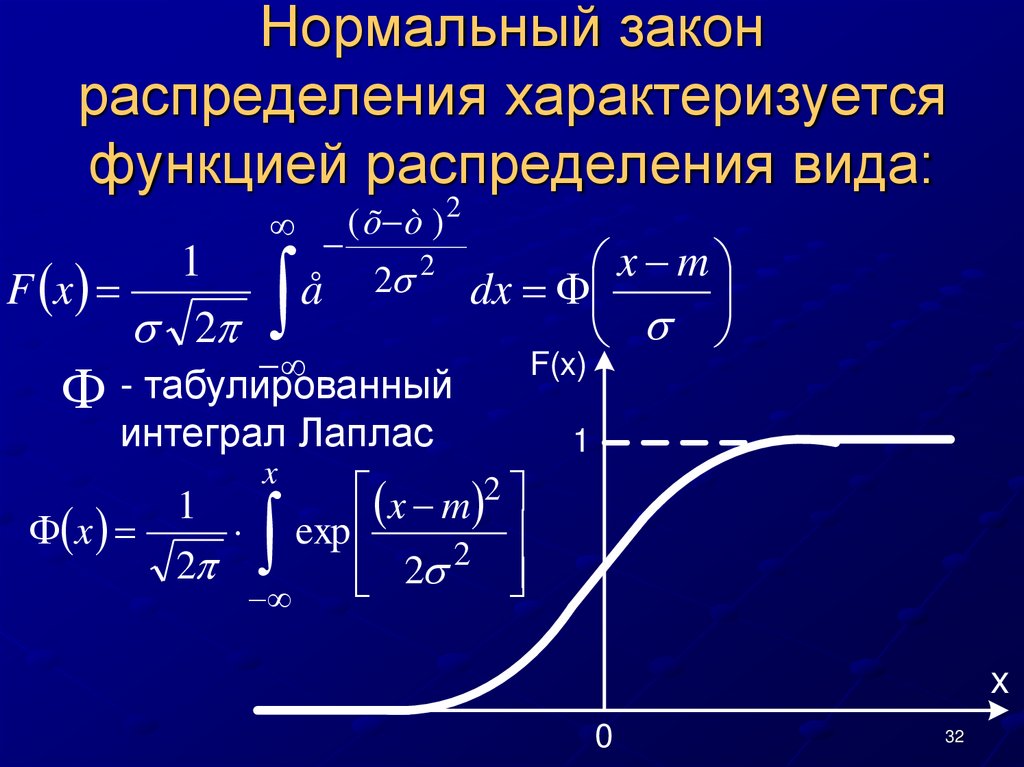
При решении статистических задач, связанных с нормальным распределением, полезно использовать таблицы стандартного нормального распределения для вычисления вероятностей.

Наглядная визуализация нормального распределения #vertdider #veritasium
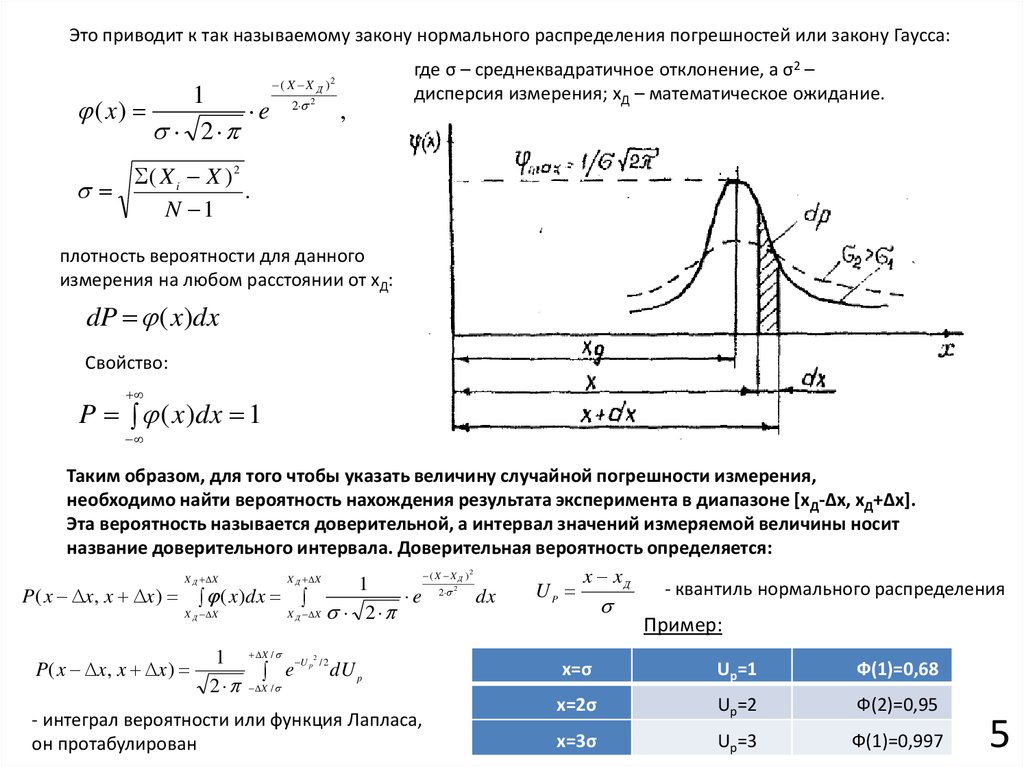
Интегральная кривая нормального распределения часто используется в тестах, таких как t-тест, для оценки статистической значимости.
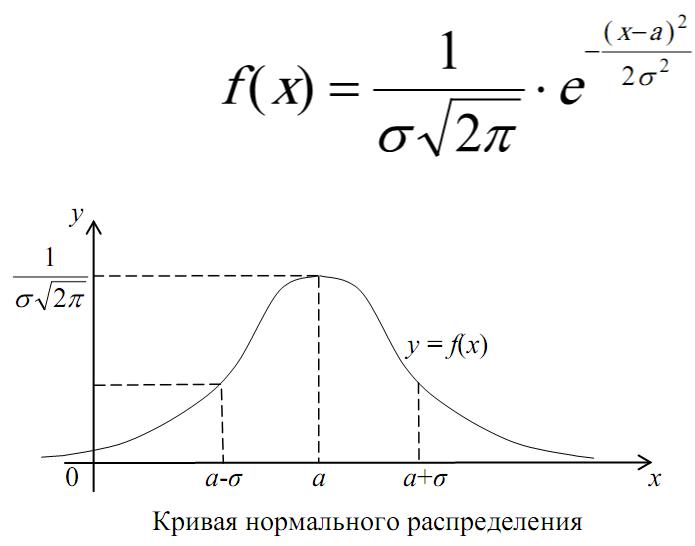
Обратите внимание, что стандартное нормальное распределение всегда имеет среднее значение, равное нулю, и стандартное отклонение, равное единице.

Нормальное Распределение за 6 Минут
При работе с большими данными полезно использовать интегральную кривую для понимания того, как данные распределяются вокруг среднего значения.

Теория вероятностей #12: случайная величина, плотность и функция распределения
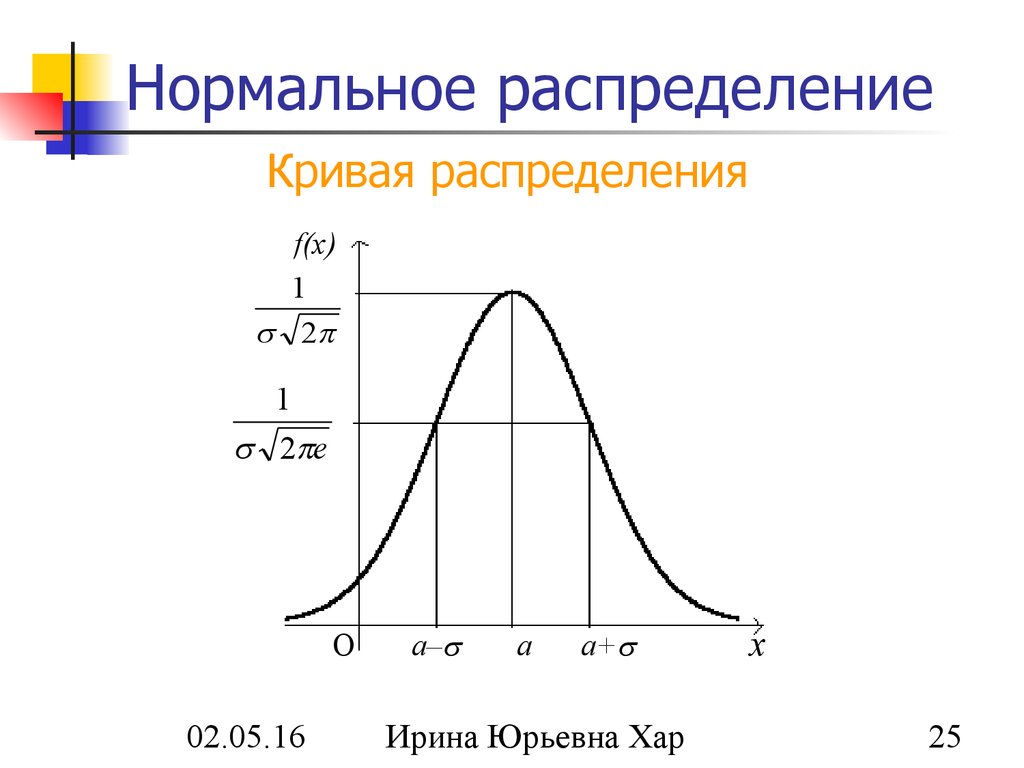

Нормальное распределение используется в различных областях, таких как экономика, медицина и инженерия, для предсказания вероятных исходов событий.

Экспоненциальный закон распределения
Для более глубокого анализа важно не только построить график кривой, но и использовать её в контексте других статистических методов, например, корреляции или регрессии.