Как правильно использовать свойства хорды и диаметра окружности в геометрии
На этой странице мы рассмотрим основные свойства хорды и диаметра окружности, а также дадим полезные советы для их практического применения в геометрии. Эти знания могут быть полезны как для школьников, так и для студентов, изучающих основы математической геометрии.
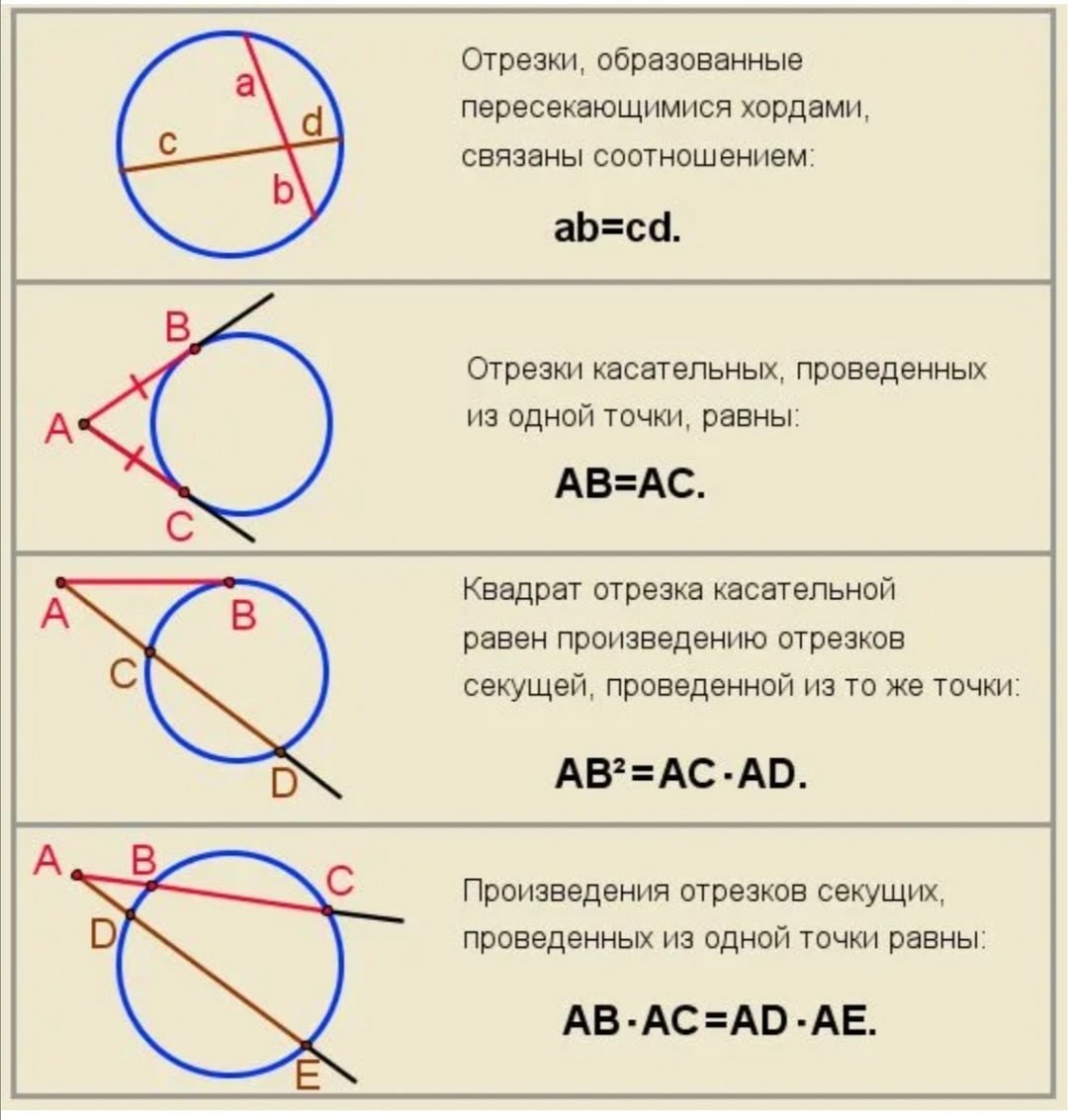


Не забывайте, что хорда окружности всегда параллельна диаметру, если она проходит через центр окружности.
Свойство диаметра окружности. 7 класс.

Запомните, что длина хорды зависит от расстояния от её середины до центра окружности: чем ближе середина хорды к центру, тем длиннее хорда.

Окружность. Круг. Радиус,диаметр, хорда. Длина окружности и дуги окружности. Сборник тестов. DİM2023
Если две хорды окружности равны, то расстояние от их середин до центра окружности будет одинаковым.

Как Найти Радиус Сегмента на Потолке. Радиус Окружности По Хорде И Высоте Сегмента
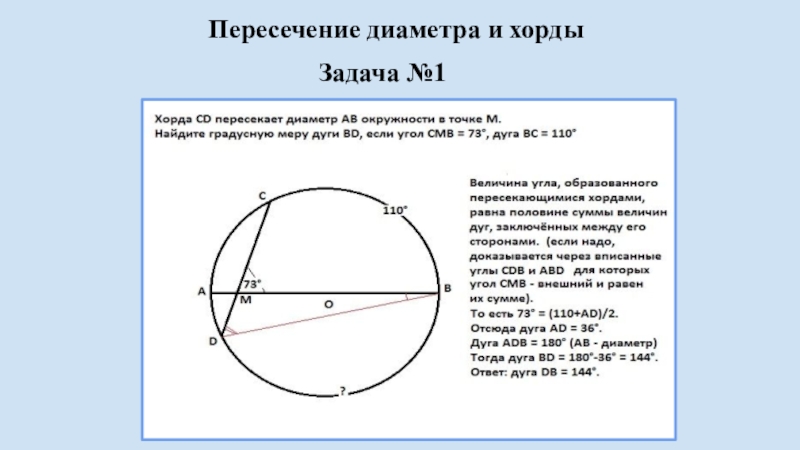
Диаметр окружности всегда является максимальной возможной хордой этой окружности, и он делит окружность на две равные части.

Окружность, диаметр, хорда геометрия 7 класс
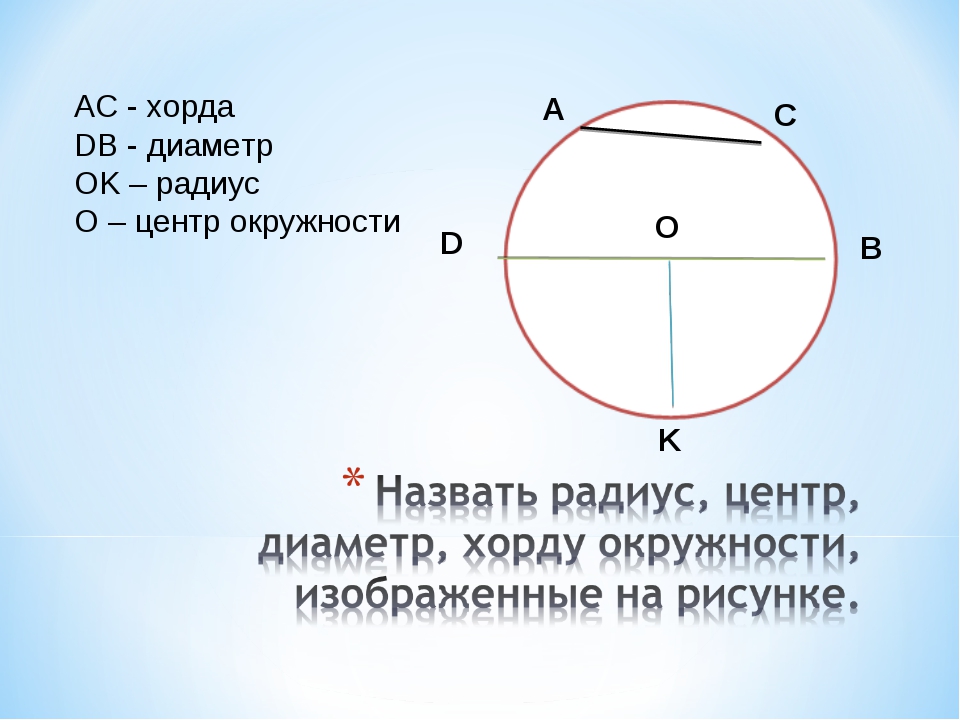
Чтобы найти длину хорды, можно использовать теорему о перпендикуляре, опущенном из центра окружности на хорду: он делит её пополам.

Окружность. 7 класс.
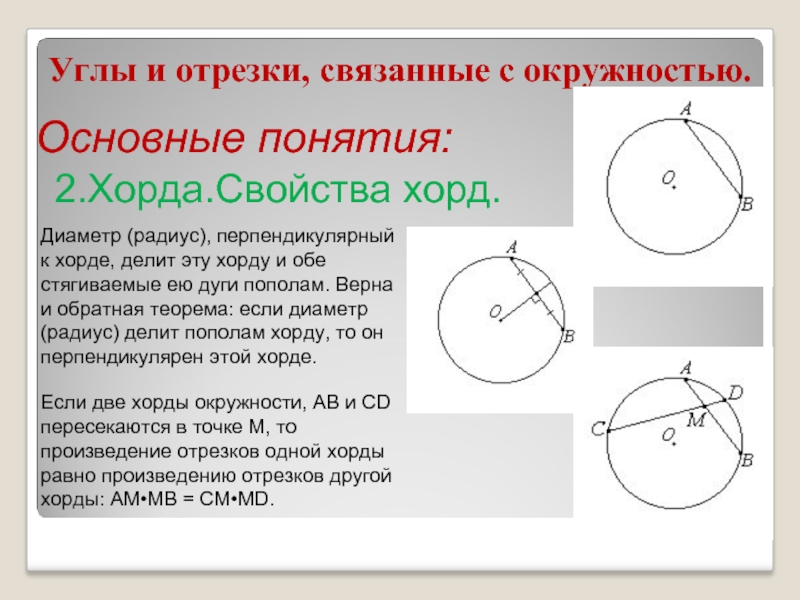
При пересечении двух хорд окружности, произведение отрезков каждой хорды будет одинаковым, если хорд пересекаются внутри окружности.

Как разделить окружность на равные части.
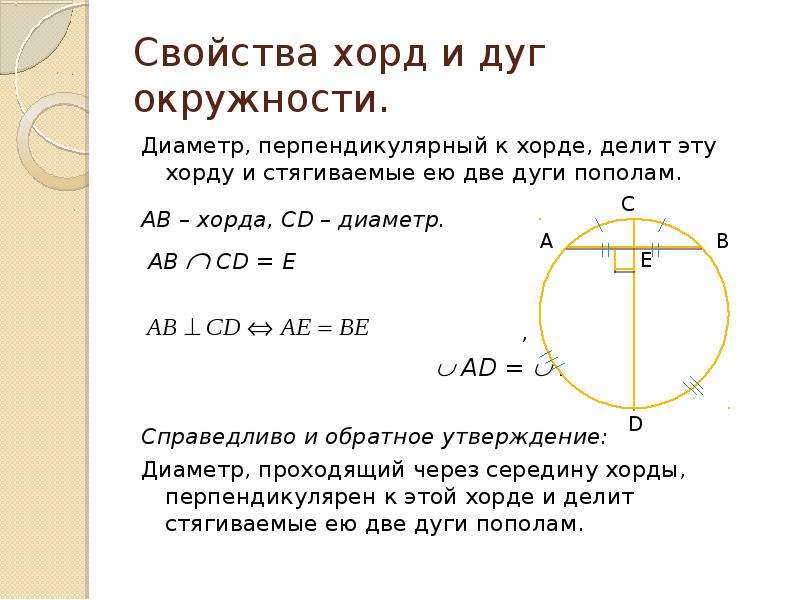

Для вычисления длины хорды, которая не проходит через центр окружности, используйте формулу, основанную на радиусе и расстоянии от центра до хорды.
Помните, что все хорды окружности, имеющие одинаковую длину, расположены на одинаковом расстоянии от центра окружности.
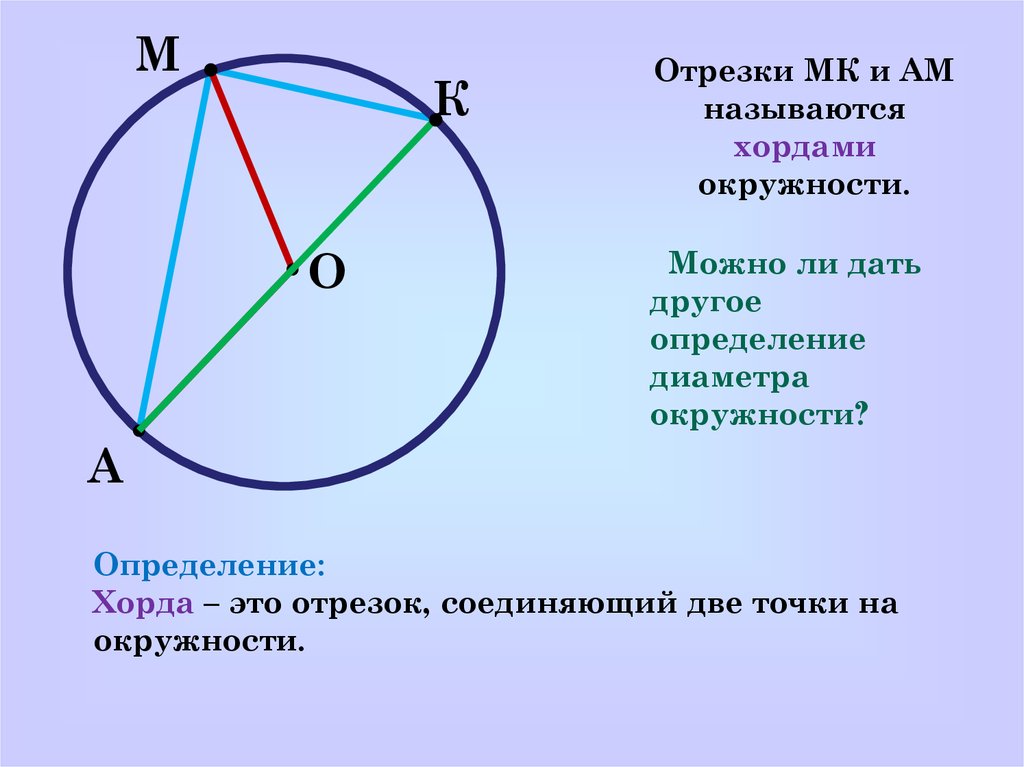
Если хорда и диаметр окружности пересекаются, то точка пересечения будет серединой хорды, и угол между ними будет прямым.
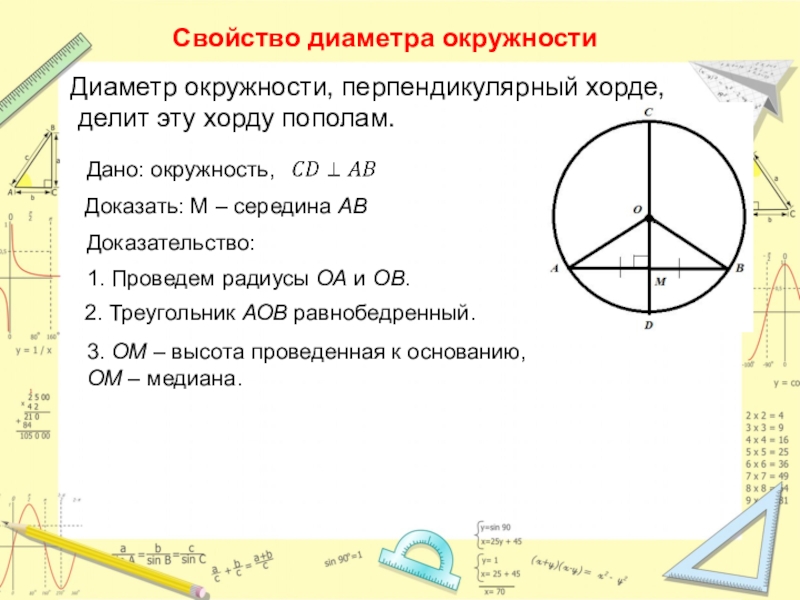
При заданных двух точках на окружности, хорда, соединяющая эти точки, всегда меньше диаметра, но может быть больше, чем радиус.
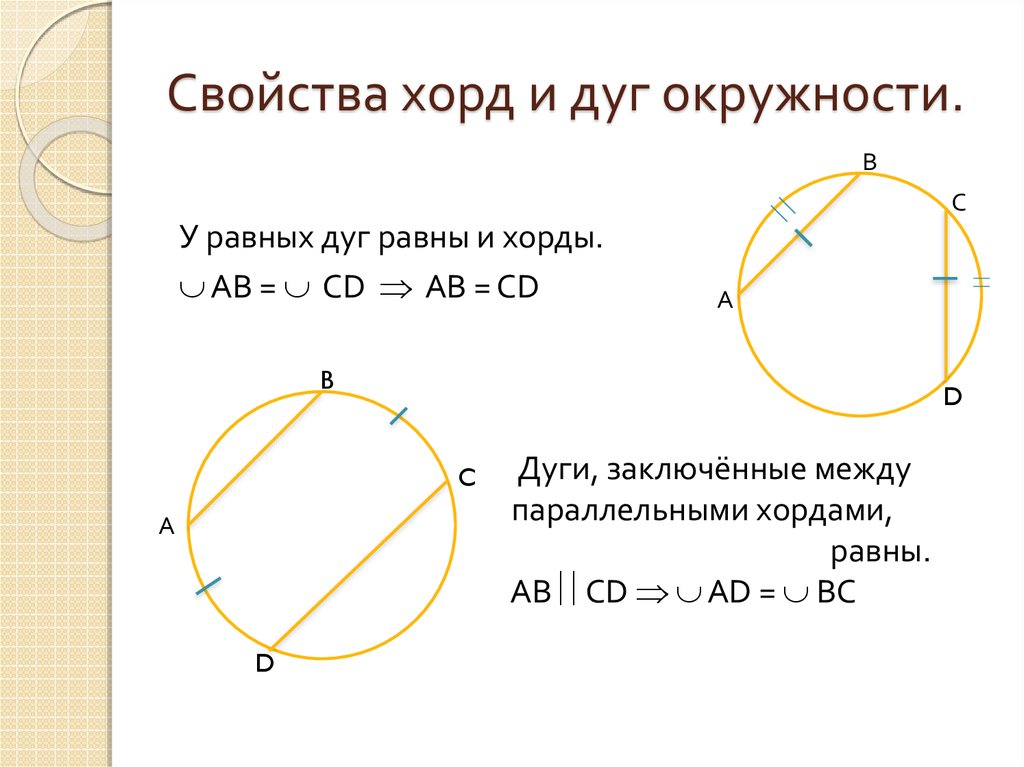

Окружность. Радиус, диаметр, хорда, длина окружности