Графики пределов функций на бесконечности: ключевые подходы и примеры

Страница посвящена построению графиков пределов функций на бесконечности. Здесь вы найдете пошаговые инструкции, полезные советы и методы, которые помогут правильно визуализировать поведение функции при стремлении аргумента к бесконечности. Мы разберем различные типы пределов и их графическое отображение, а также предоставим полезные примеры.

Для правильного построения графика важно сначала определить вид функции и её асимптоты, так как они играют ключевую роль в поведении функции на бесконечности.

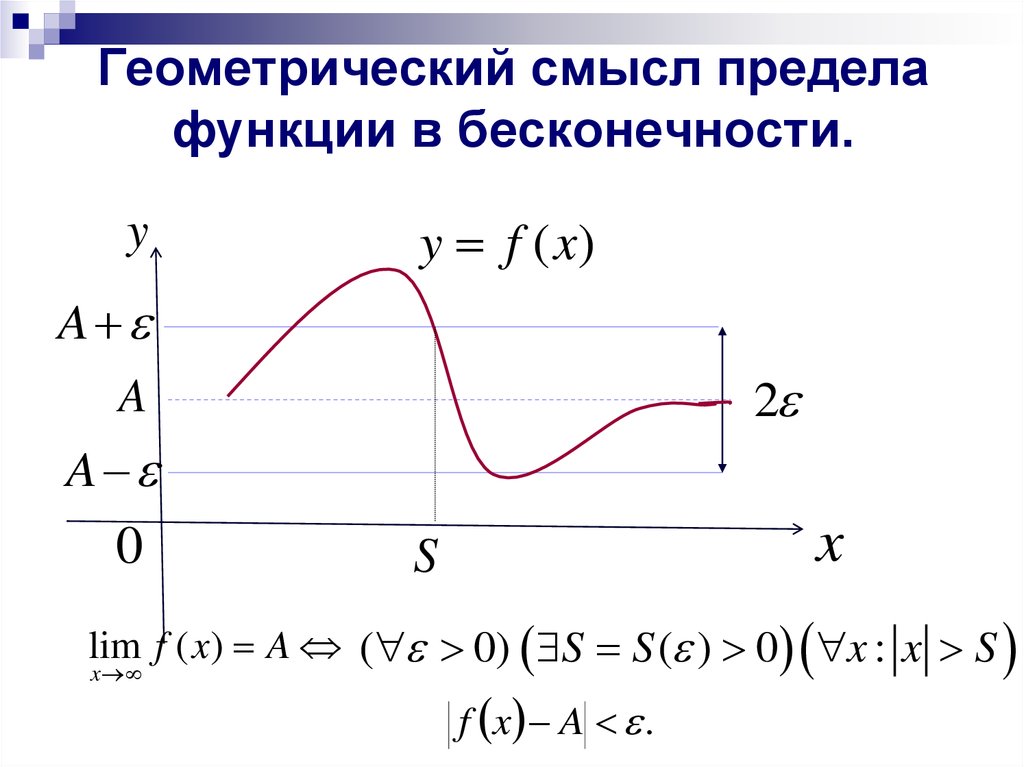
Обратите внимание на тип предела: если функция стремится к конечному значению, это может означать горизонтальную асимптоту, а если к бесконечности — вертикальную или наклонную асимптоту.

Начинайте построение графика с анализа поведения функции на больших значениях x, так как именно здесь будет видно, как она приближается к своему пределу на бесконечности.

Для функций с полиномами в числителе и знаменателе важно учитывать степень этих полиномов, так как она определяет конечное значение предела или наличие асимптоты.

При работе с рациональными функциями учитывайте возможные вертикальные асимптоты, которые могут возникать при значении x, где знаменатель равен нулю.

Если предел функции на бесконечности не существует, стоит обратить внимание на поведение функции на очень больших значениях x, чтобы понять, растет ли она безогранично или колеблется.

Используйте вспомогательные графики, чтобы увидеть, как функция ведет себя на больших значениях аргумента, и помочь себе при построении общего графика.

Для функций с экспоненциальным или логарифмическим видом характерно быстрое изменение значения функции на бесконечности, что необходимо учитывать при построении графиков.

Не забывайте о возможных изменения направления графика, если функция имеет периодические компоненты, что может повлиять на пределы при стремлении к бесконечности.

Регулярно проверяйте свои графики, используя различные методы, например, анализ пределов с использованием производных или симметричных функций для более точного отображения.