Как правильно определять ключевые точки и элементы круговой кривой
Круговая кривая — важный элемент в геометрии и проектировании. Правильное определение ключевых точек и элементов этой кривой помогает точно анализировать ее свойства и использовать ее в различных областях. Здесь собраны основные моменты, которые помогут разобраться в круговых кривых, а также полезные советы для их применения.
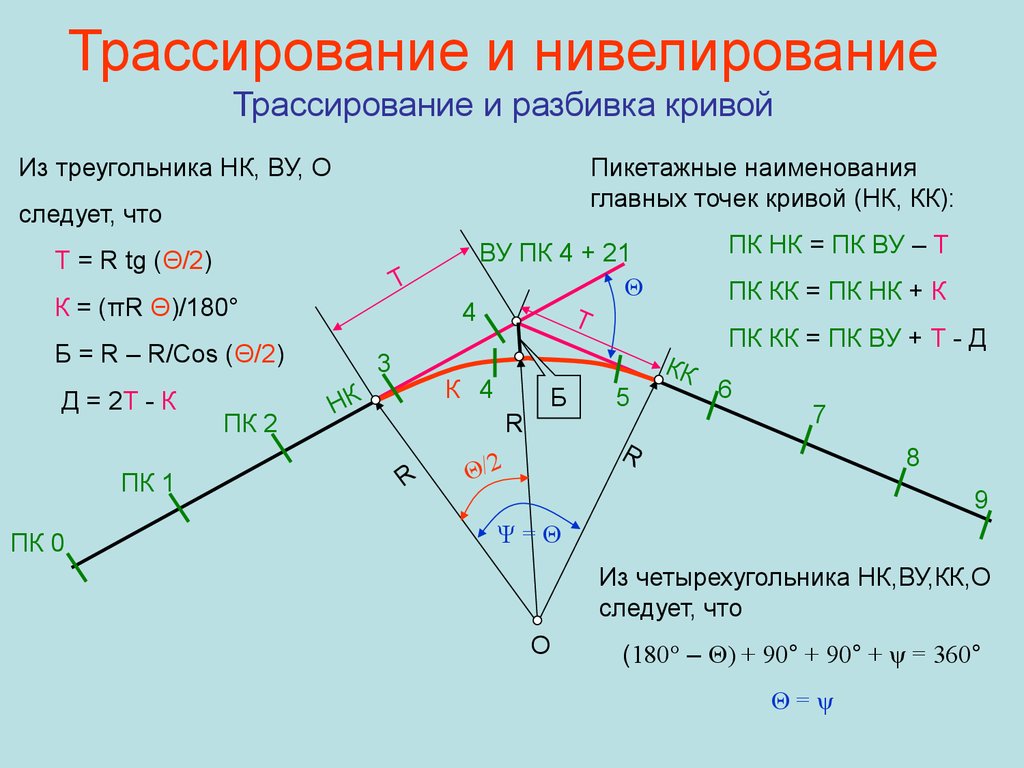

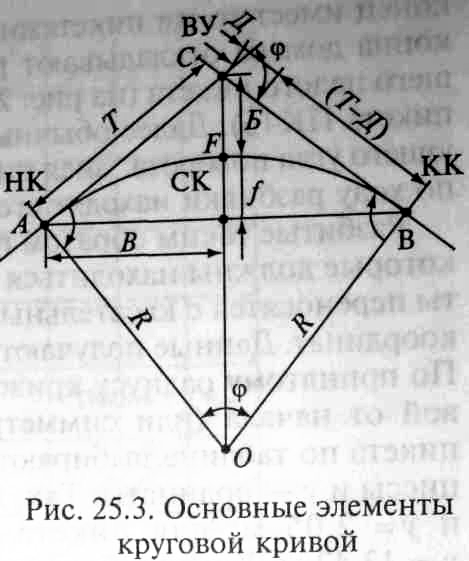
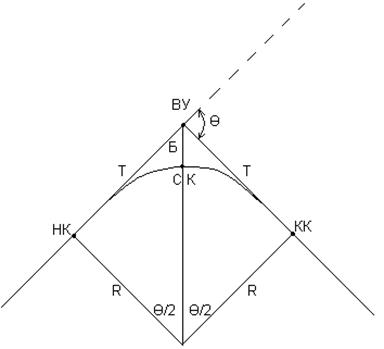
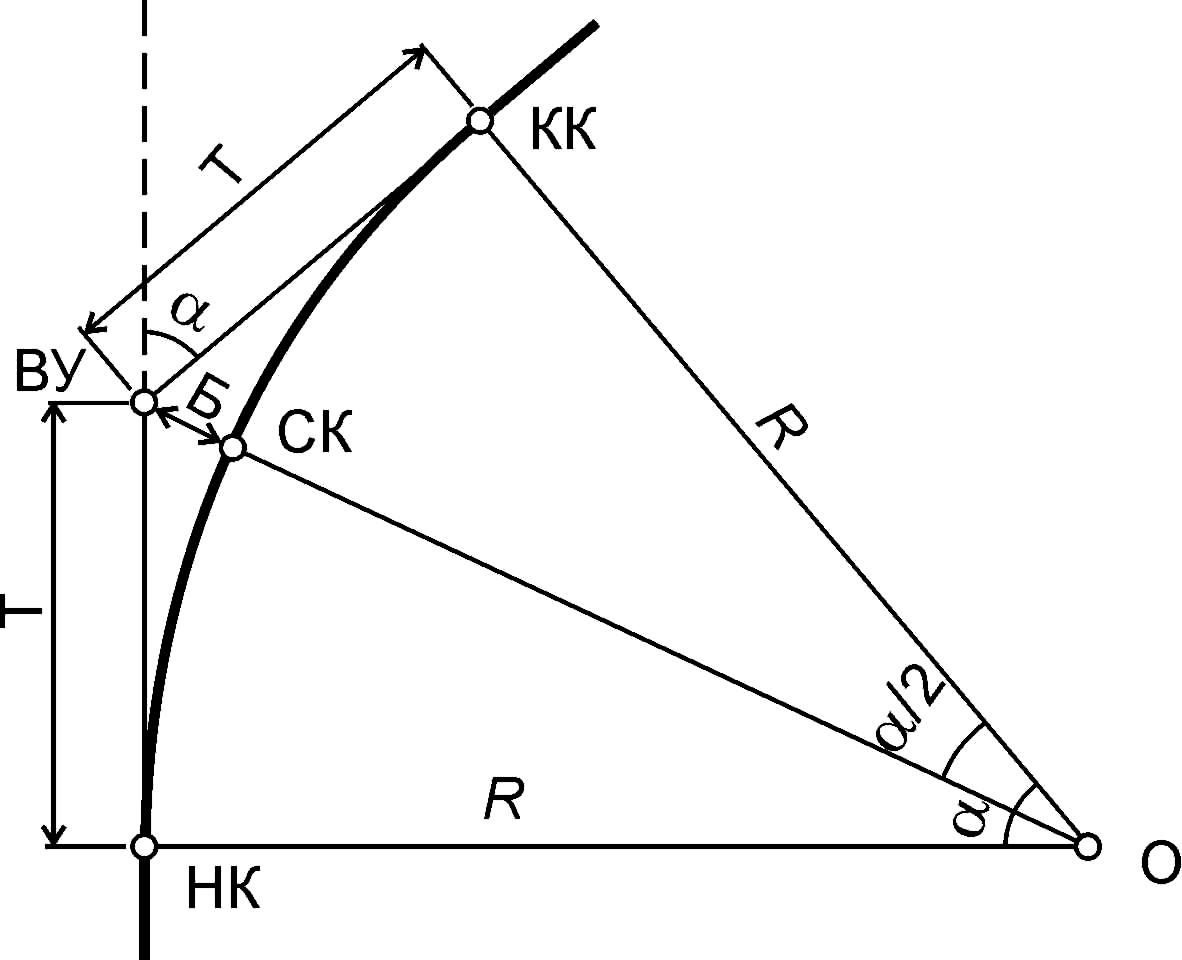
Не забывайте, что главные точки круговой кривой — это её центр и точка пересечения с осями.
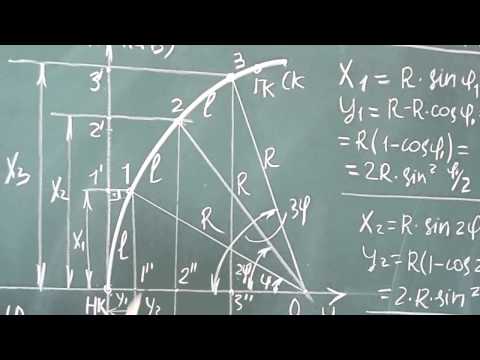
Детальная разбивка круговой кривой способом прямоугольных координат от тангенсов Д-11, 14.05.14
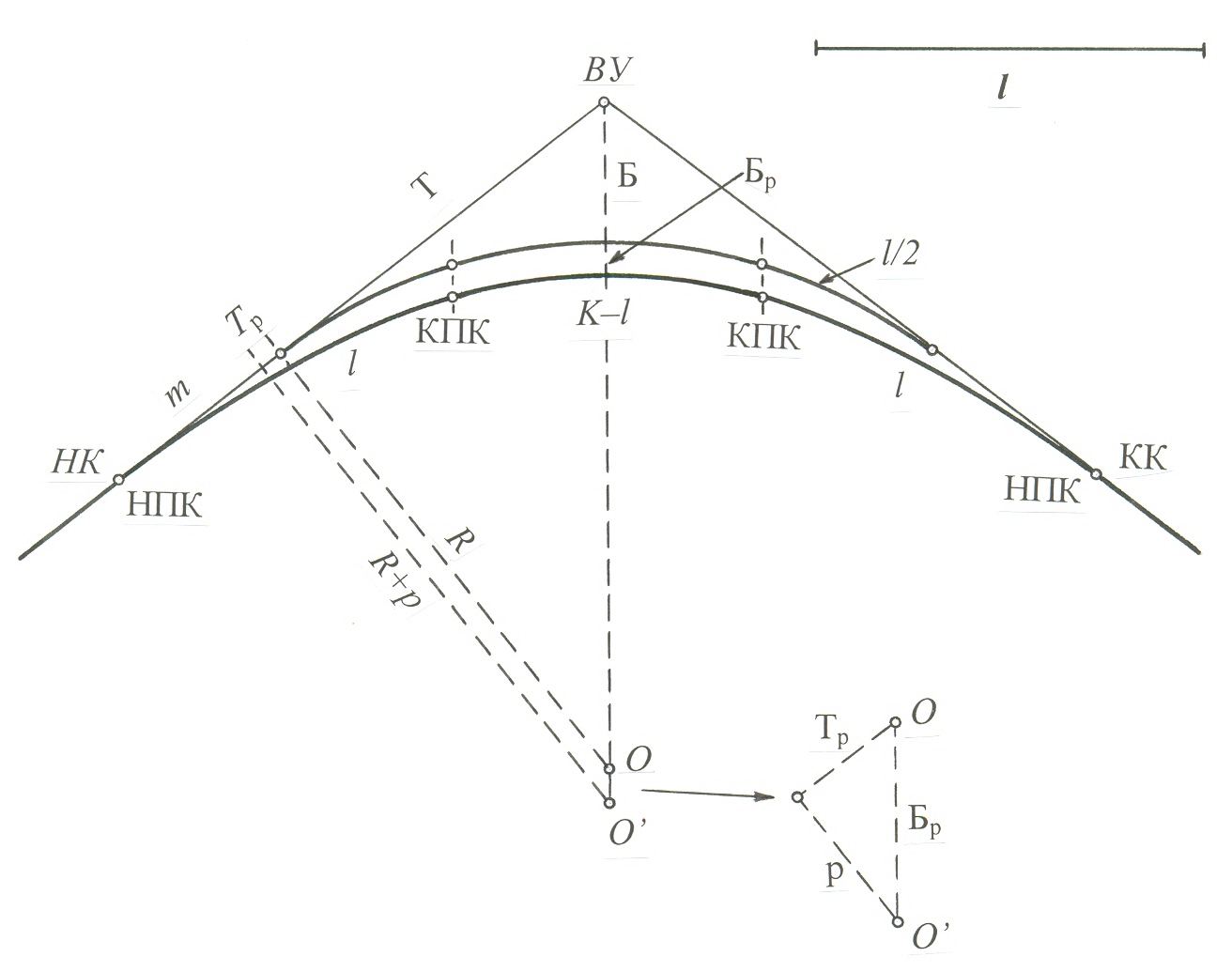
При работе с круговыми кривыми важно точно измерять радиус, поскольку это влияет на все остальные параметры.

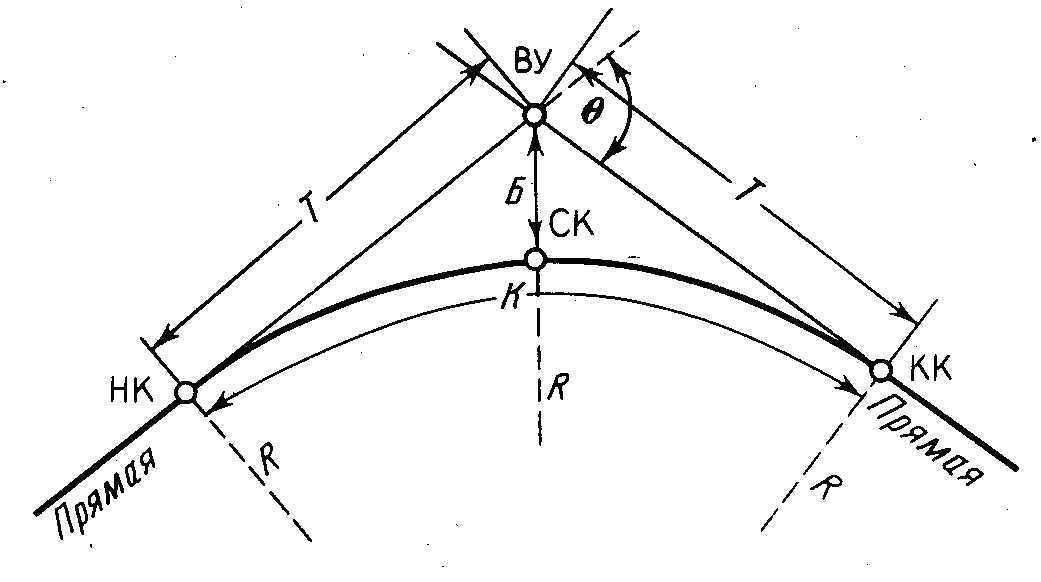
Подготовка разбивочных элементов и разбивка на местности круговой кривой

Используйте геометрические инструменты для точной отрисовки кривых и проверки их симметрии.
Часть 1. Расчет основных элементов круговой кривой
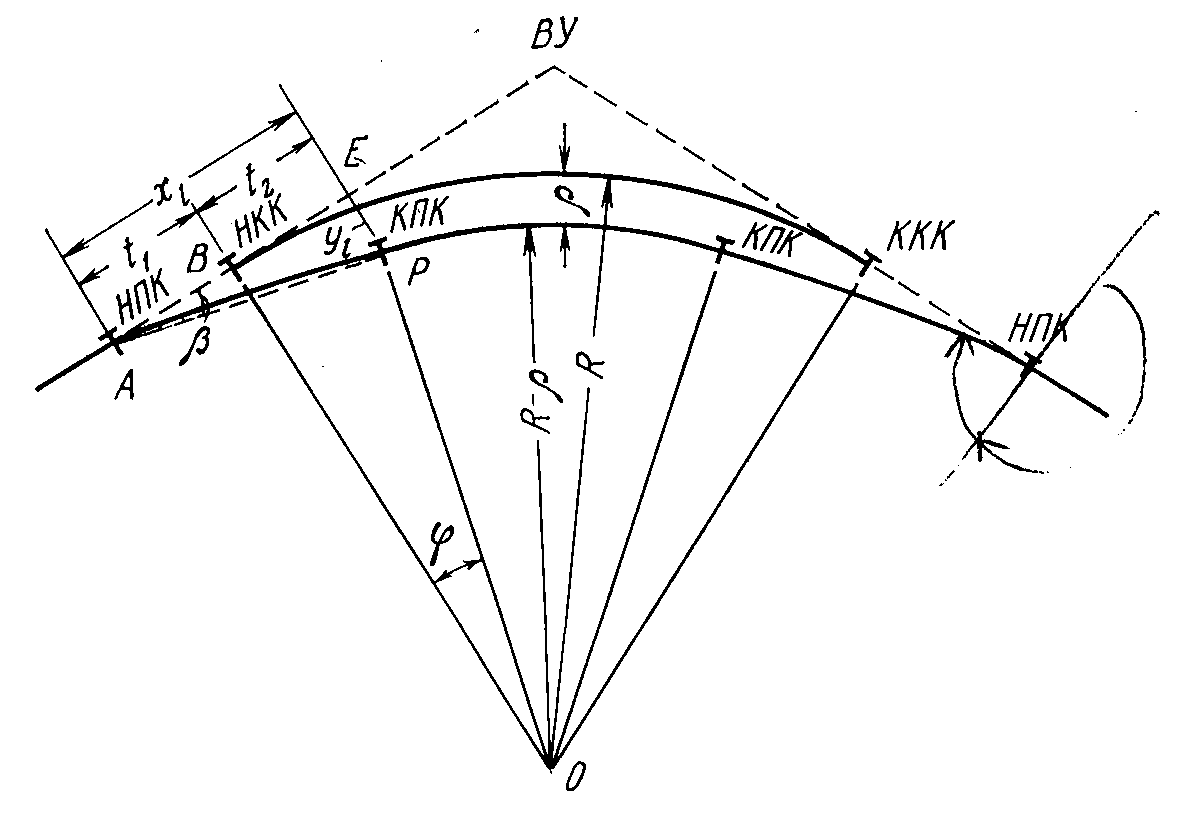
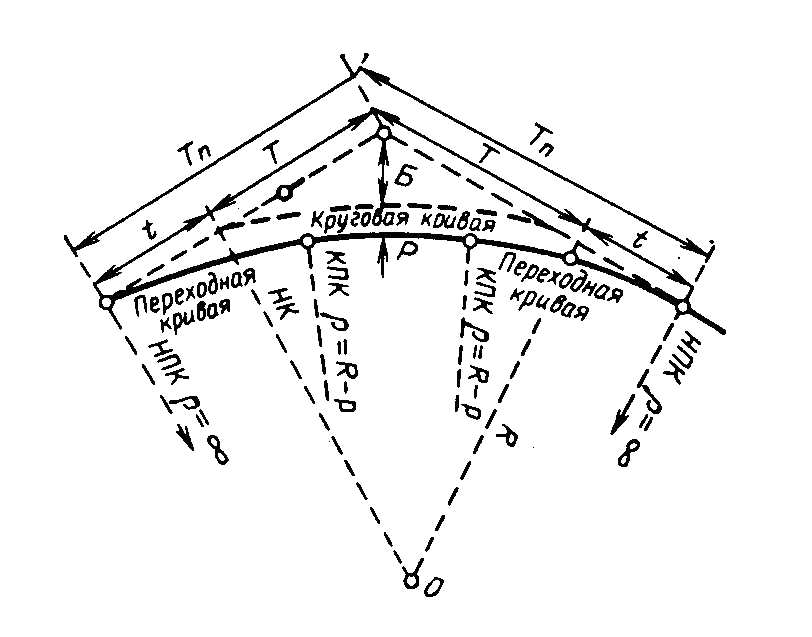
Помните, что круговые кривые часто используются в проектировании дорог и путей, где точность критична.

Какую форму имеет точка в геометрии
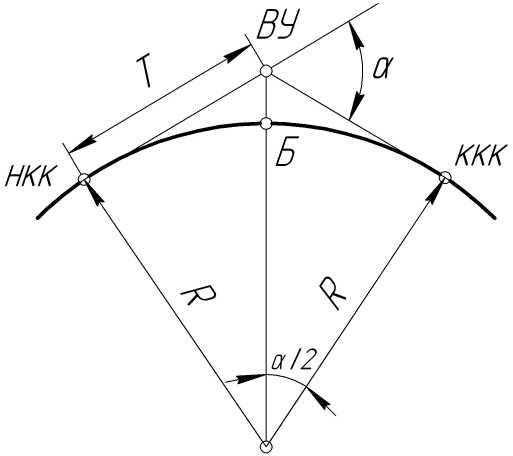
При анализе круговой кривой учитывайте её радиус кривизны, который помогает определять её геометрическую характеристику.

Криволинейное, равномерное движение материальной точки по окружности. 9 класс.
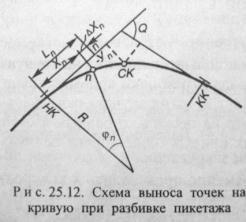

Для практических целей часто применяют приближенные методы для вычисления ключевых точек, особенно если точность не критична.
Математика без Ху%!ни. Кривые второго порядка. Эллипс.
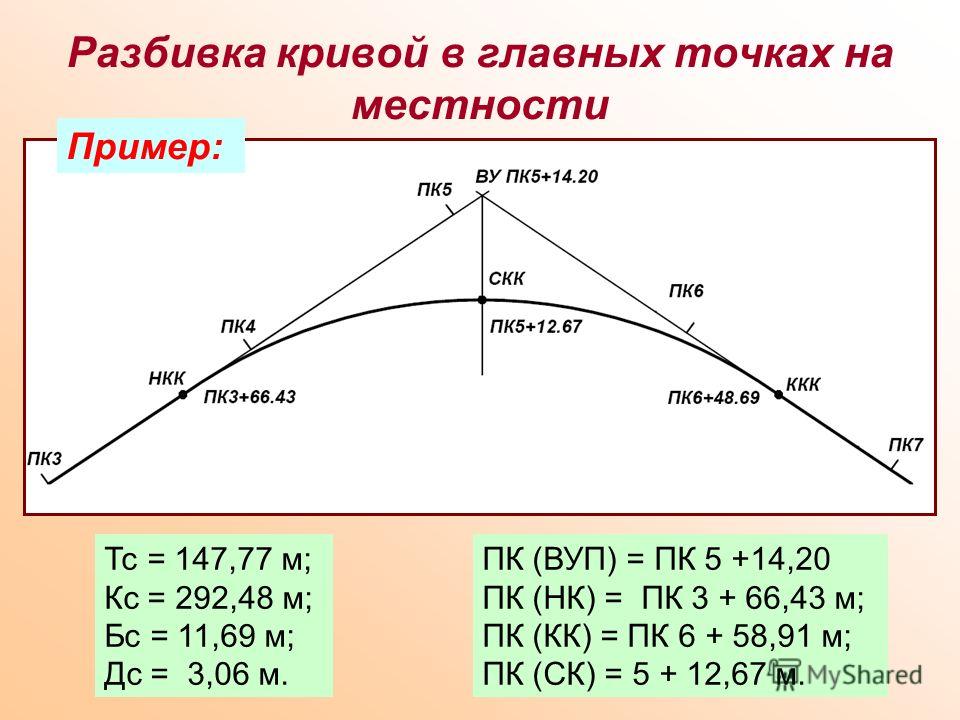
Старайтесь использовать чертежи и схемы для визуализации кривой и её элементов, это ускоряет понимание процесса.

Обратите внимание на особенности перехода между круговыми кривыми и прямыми участками, это важный момент в проектировании.
Работая с круговыми кривыми, учитывайте возможные ошибки при измерении углов, которые могут повлиять на точность расчётов.

Построение плана трассы. Элементы круговой кривой. Главные точки кривой при повороте

Не забывайте, что на практике круговые кривые могут деформироваться, поэтому всегда проверяйте результаты с использованием разных методов анализа.