Понимание функции квадратного корня и анализ ее графических характеристик
Функция квадратного корня представляет собой одну из базовых математических функций, с которой сталкиваются ученики и студенты при изучении алгебры. Ее график, свойства и поведение могут быть полезными в решении множества математических задач. В этой статье мы рассмотрим основные аспекты функции квадратного корня, а также дадим полезные советы по работе с ней.

При решении задач, связанных с функцией квадратного корня, не забывайте о важности определения области допустимых значений, так как корень из отрицательных чисел не существует в множестве действительных чисел.

\
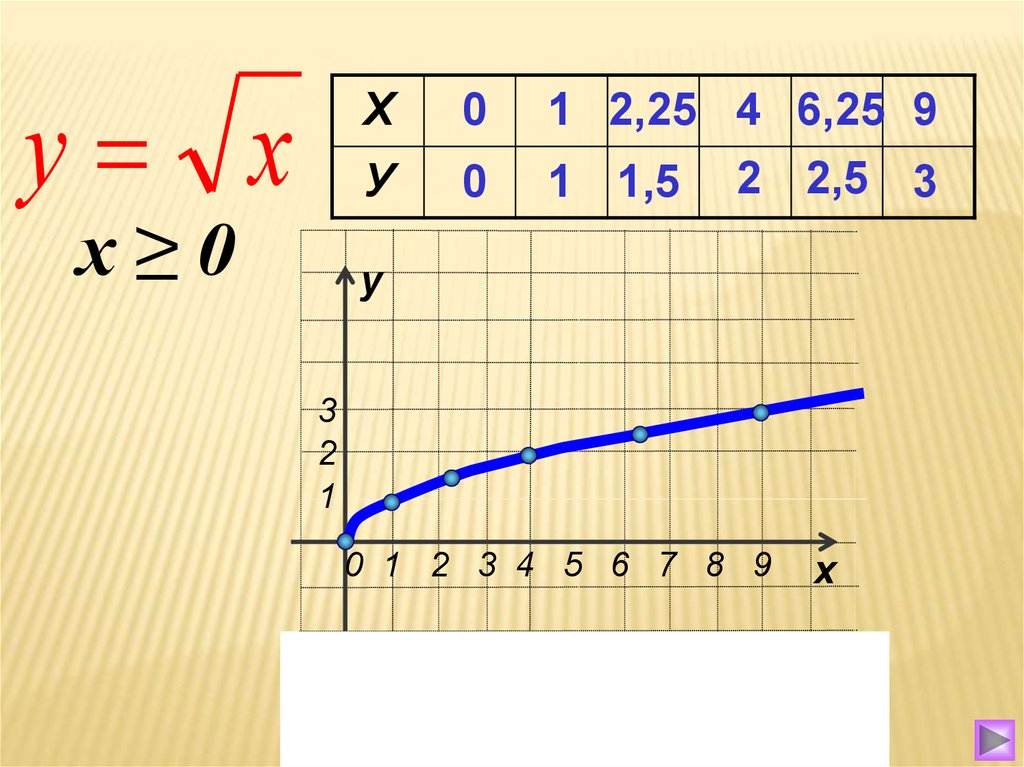
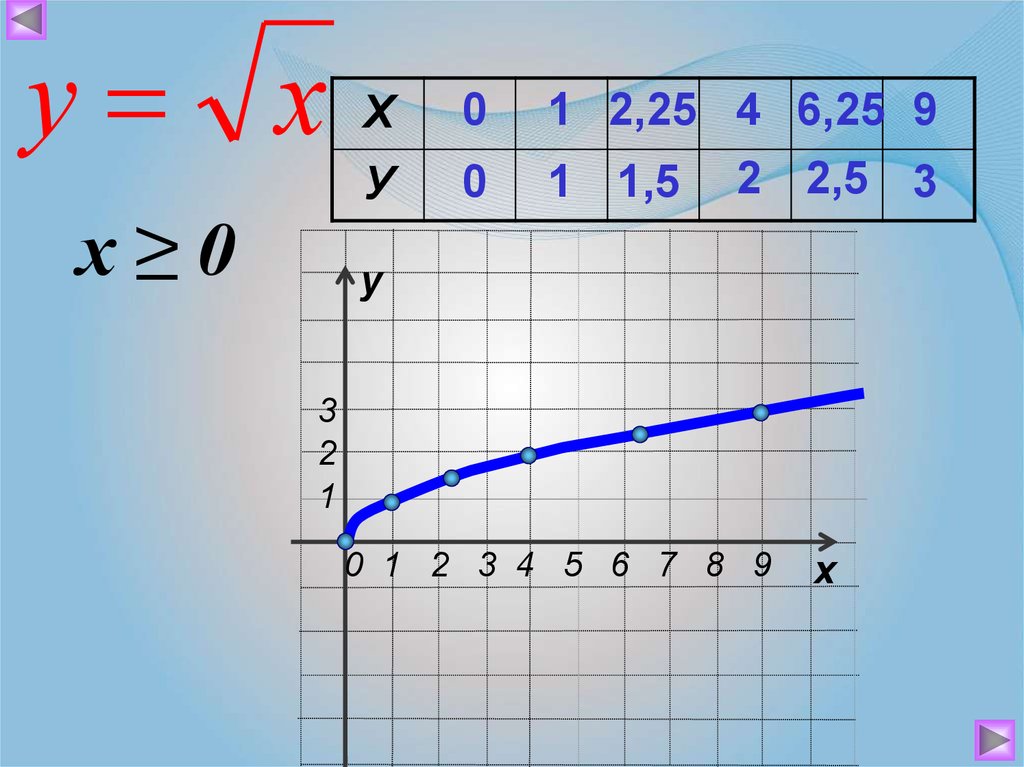
Обратите внимание, что график функции квадратного корня всегда начинается с точки (0,0), так как квадратный корень из нуля равен нулю.
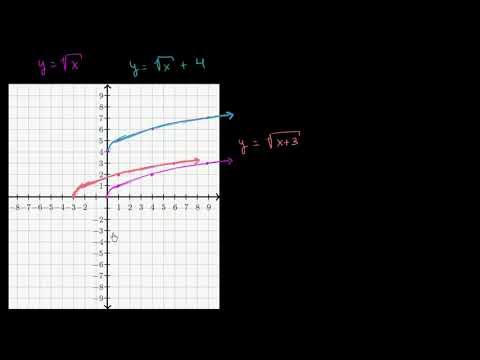
Преобразование графика функции квадратного корня - Функции и Графики - Алгебра II
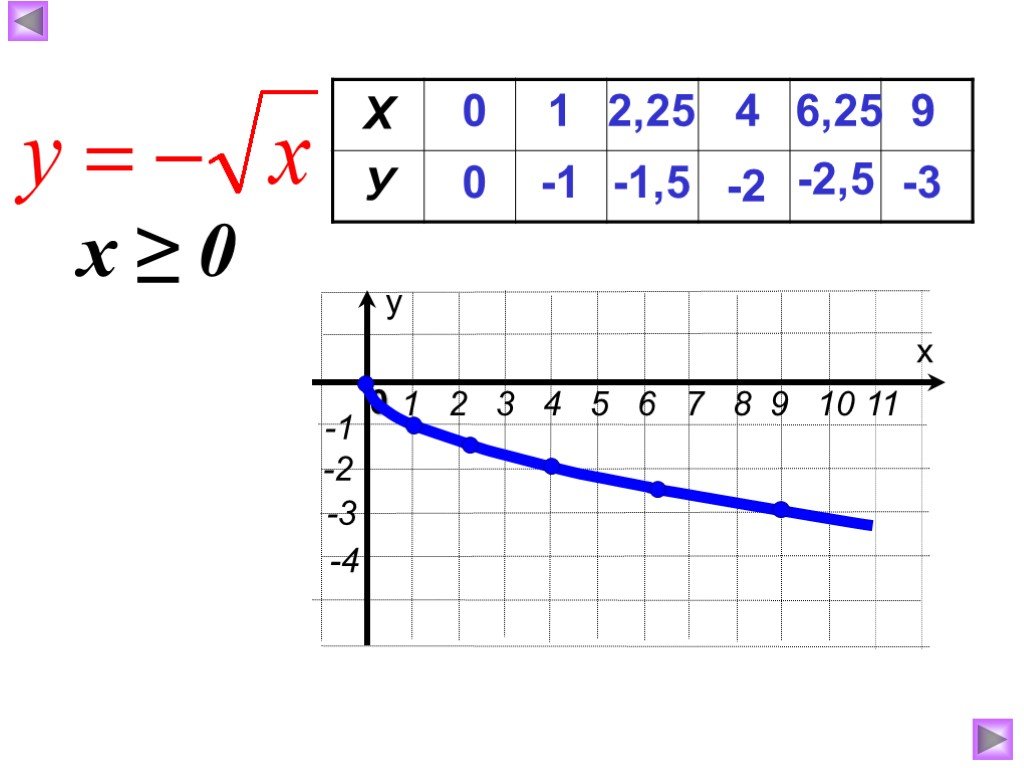
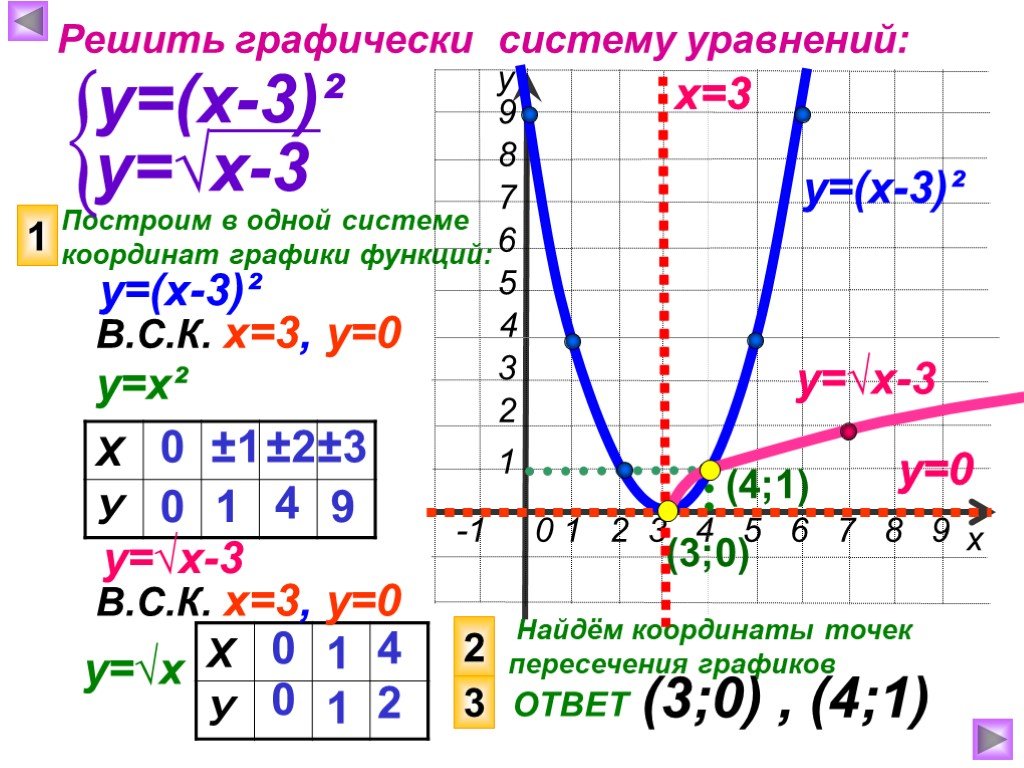
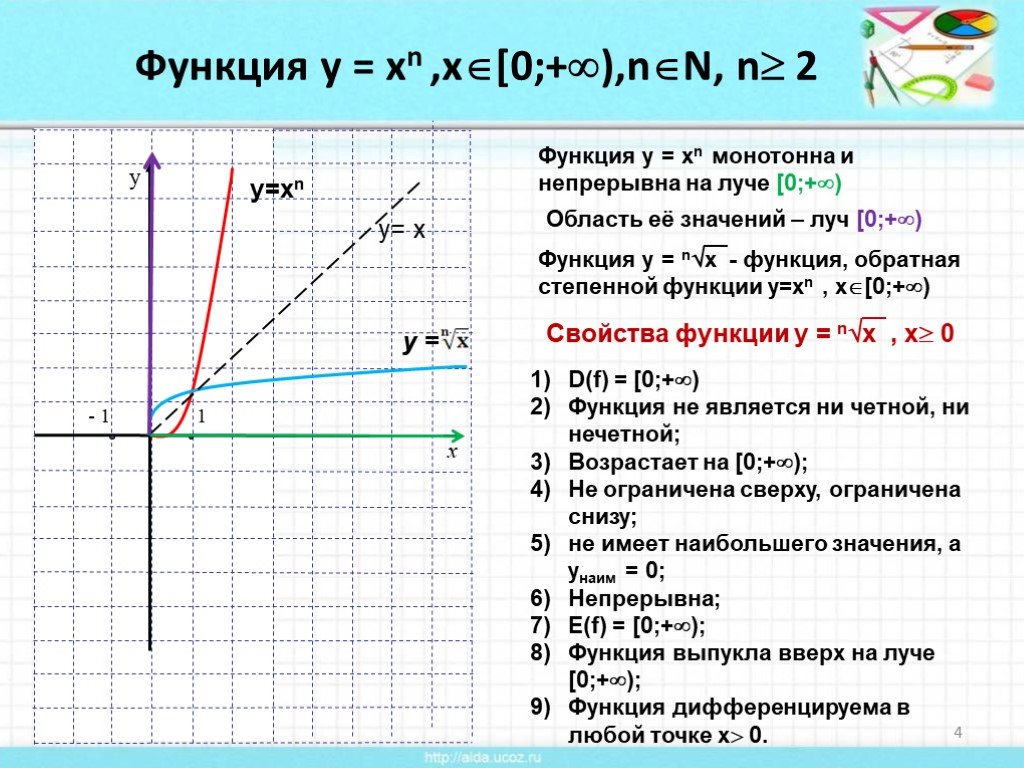
График функции квадратного корня является возрастающей кривой, которая постепенно приближается к прямой, но никогда не пересекает ось абсцисс.
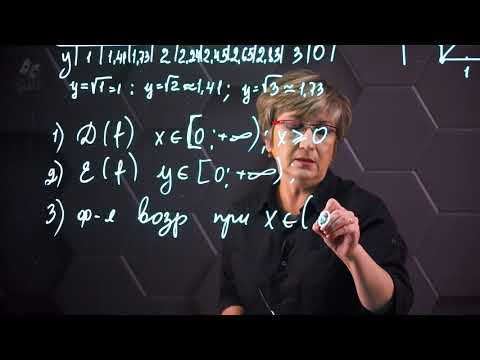
Функция y=√x, ее свойства и график. 8 класс.

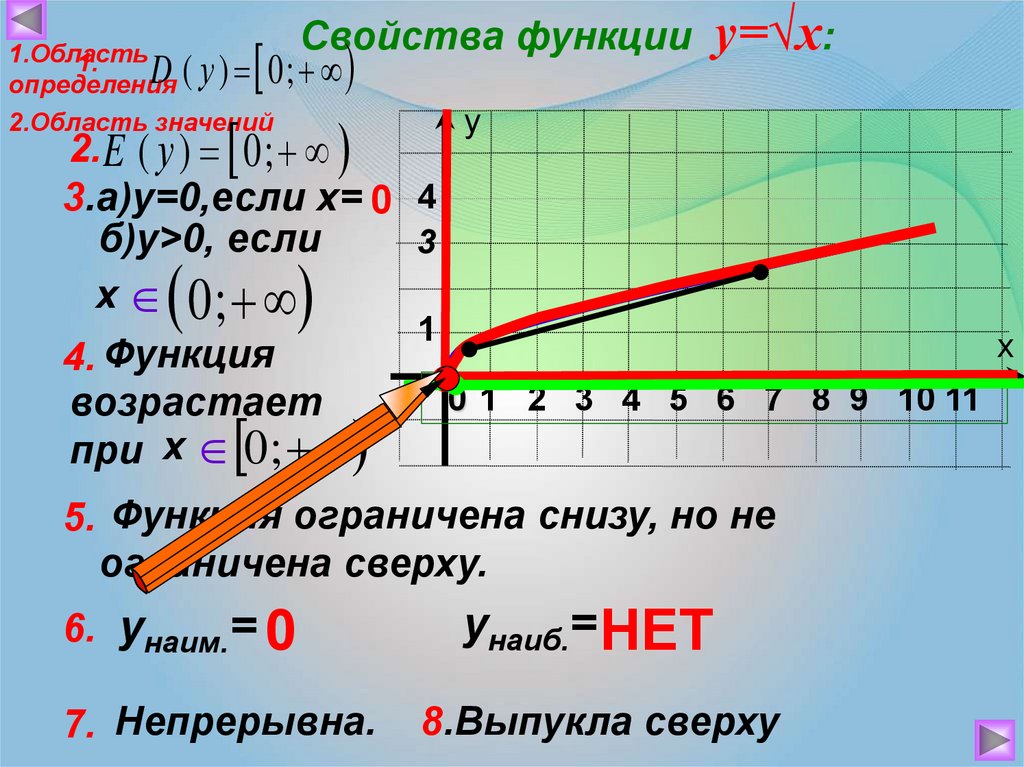
Функция квадратного корня всегда принимает только положительные значения или ноль, так как корень из отрицательного числа не имеет смысла в действительных числах.

Функция y = √x, ее свойства и график . §18 алгебра 8 класс
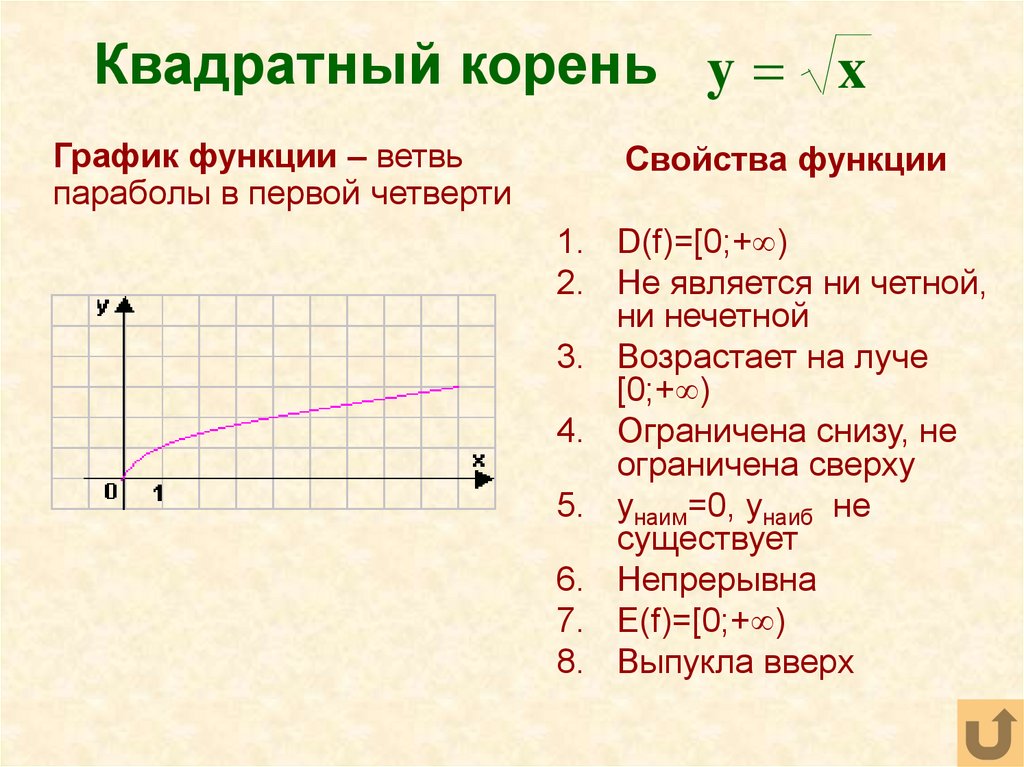
Важно помнить, что если вы работаете с выражениями вида √(x), то всегда учитывайте, что x должно быть больше либо равно нулю, иначе выражение не будет определено.

Функция квадратного корня, его график и свойства (1) Функция корень из x

График функции квадратного корня можно представить как полукривую, расположенную в первой четверти координатной плоскости, что указывает на ее положительное значение для всех x ≥ 0.

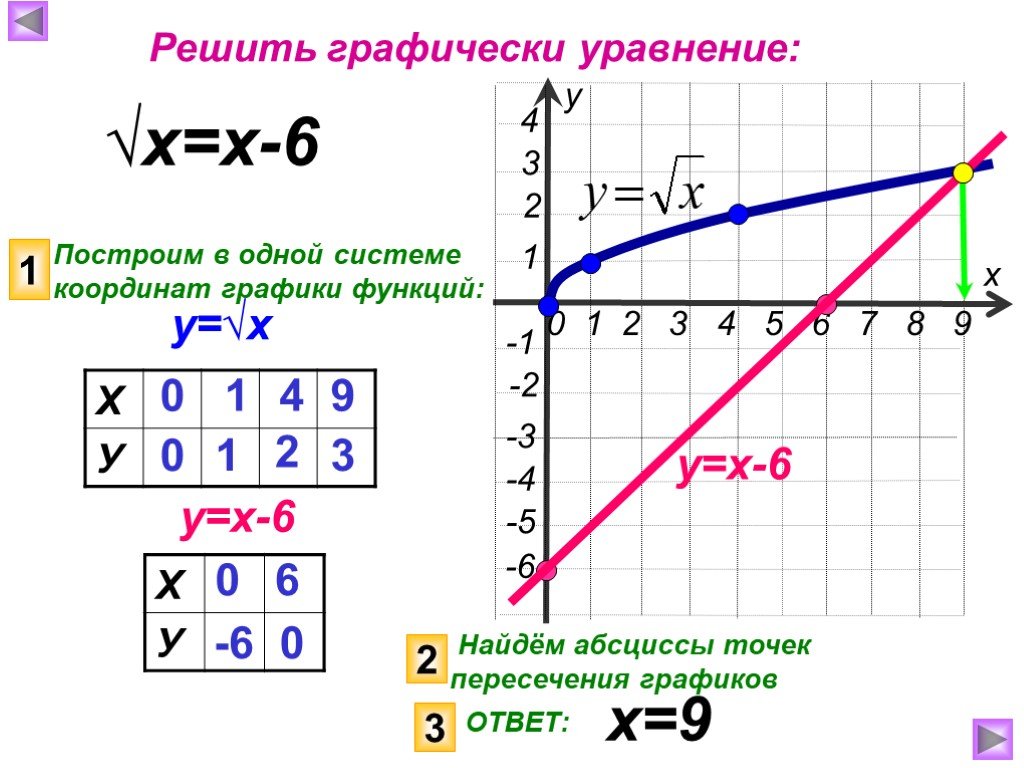
Для того чтобы быстро графически представить функцию квадратного корня, можно воспользоваться таблицей значений, в которой для нескольких x вычислены соответствующие значения функции.
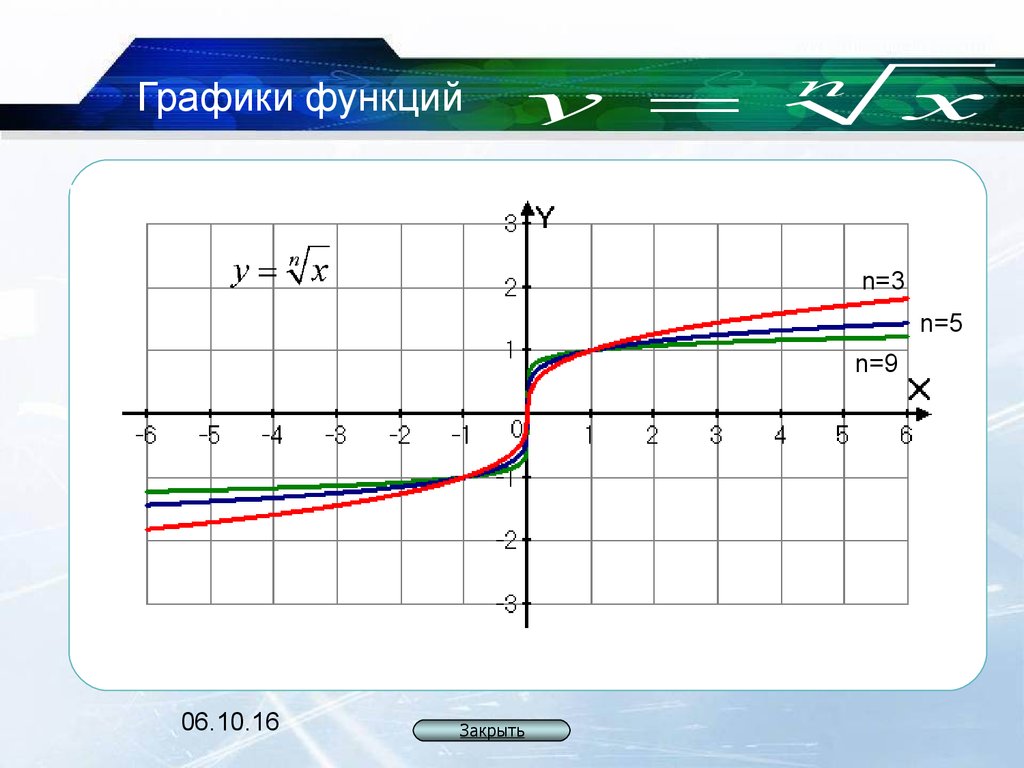
При изучении свойств квадратного корня важно также обратить внимание на его поведение при стремлении аргумента к бесконечности, когда значение функции будет увеличиваться бесконечно.

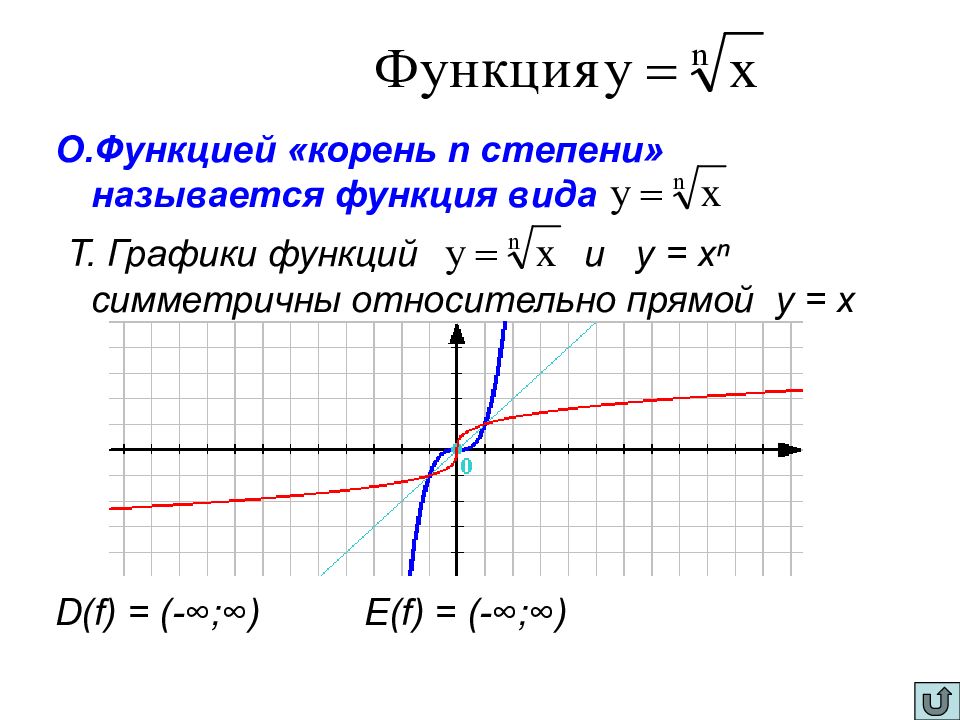
Не забывайте, что при решении уравнений с квадратным корнем иногда важно возводить обе части уравнения в квадрат для устранения корня, но при этом не забывайте проверять полученные решения на ошибки.


Решая задачи с квадратным корнем, помните, что иногда можно использовать приближенные методы или калькуляторы для вычисления значений корня, если точность не требуется.
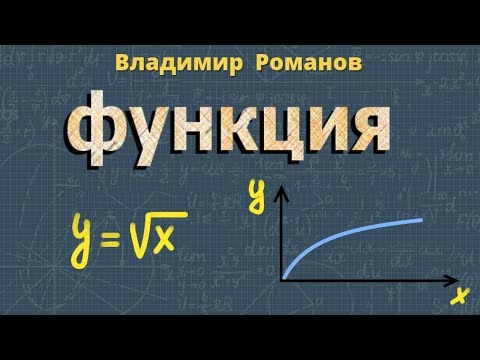
ФУНКЦИЯ y = √¯x ( корень из х ) МАТЕМАТИКА