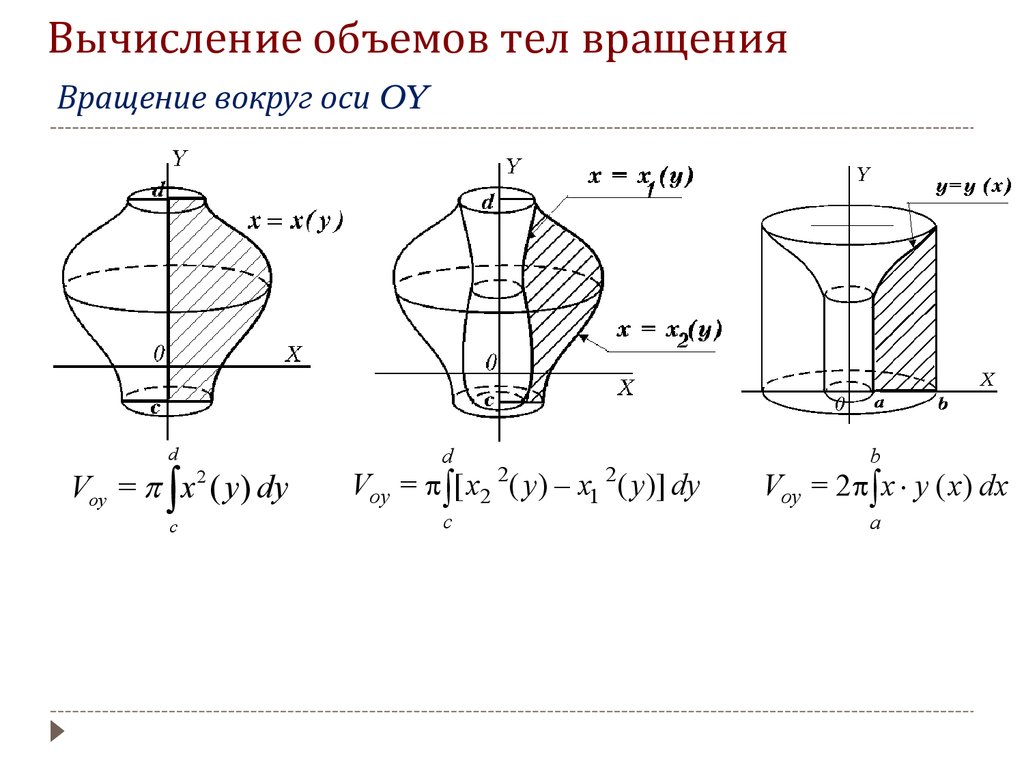
Объем с использованием интегралов: лучшие методы и рекомендации для точных расчетов
В этом разделе вы найдете подробную информацию о том, как вычислить объем геометрических фигур с помощью интегралов. Мы предлагаем наглядные примеры, теоретические объяснения и полезные советы, которые помогут вам разобраться в этом важном разделе математики.


Перед началом расчетов важно разобраться в основных формулах для нахождения объема. Знание этих основ ускорит процесс работы с интегралами.

Вычисление объемов с помощью определенного интеграла


Для вычисления объема через интеграл часто используют метод вращения, когда фигура вращается вокруг оси. Это позволяет значительно упростить задачу.

Объем через тройной интеграл
Не забывайте, что правильный выбор пределов интегрирования критически важен для получения точного результата. Внимание к деталям на этом этапе помогает избежать ошибок.
Вычисление объемов тел вращения (применение определенного интеграла)

Иногда полезно разбивать сложные фигуры на простые компоненты. Это облегчает расчет, так как для каждой части можно использовать отдельный интеграл.

Вычисление объемов тел с помощью интегралов. Урок 14. Геометрия 11 класс
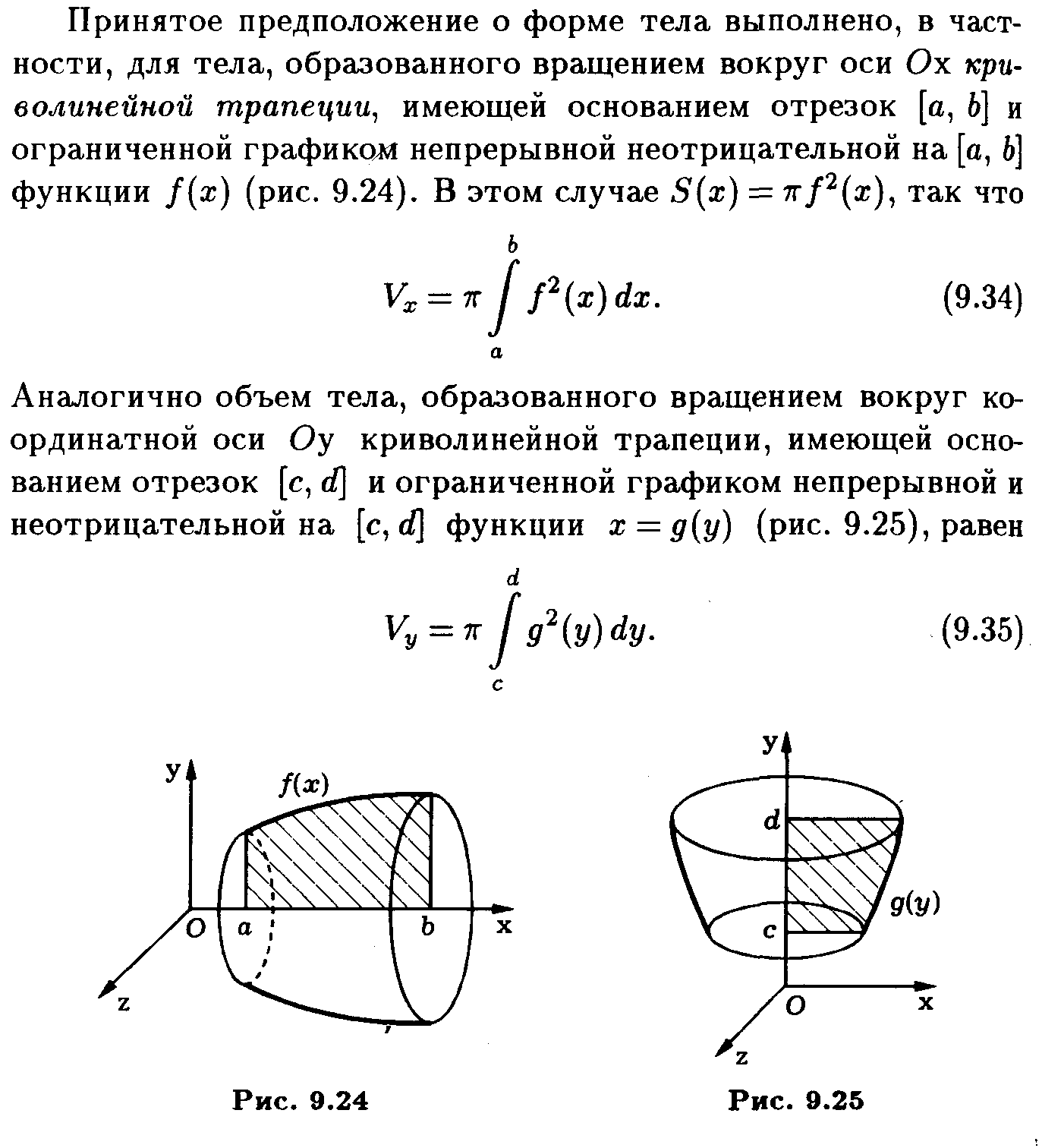
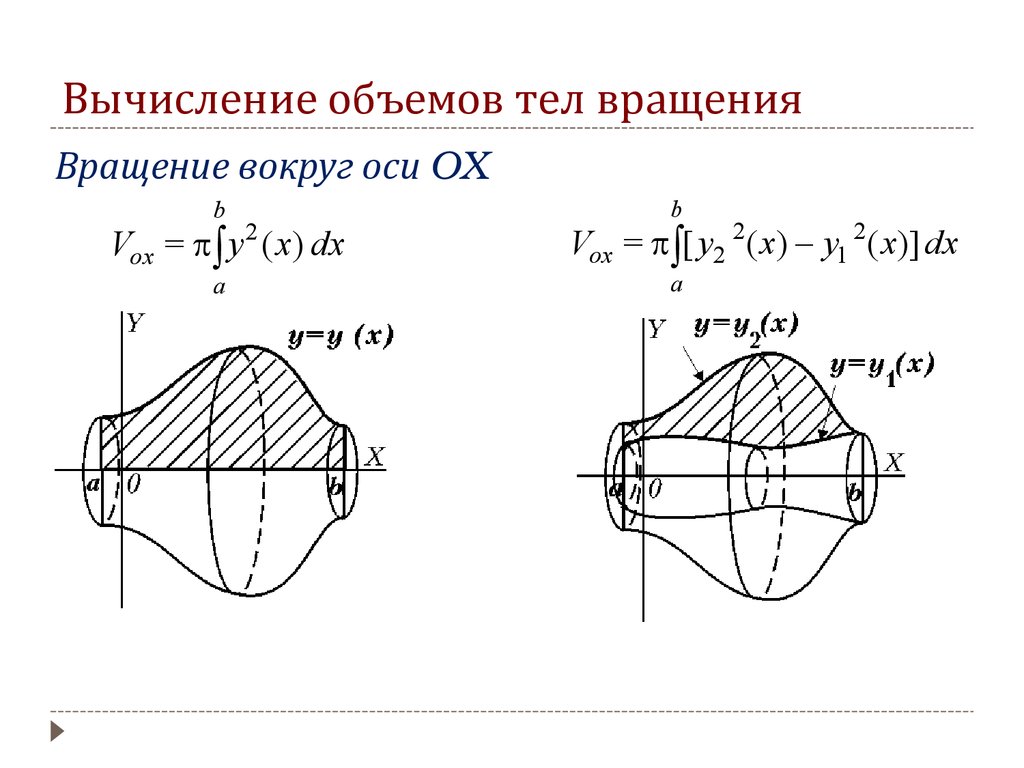
Для вычисления объема через площадь сечения убедитесь, что правильно нашли функцию, описывающую форму сечения по отношению к оси вращения.

Интегралы №13 Объем тела вращения


Не стесняйтесь использовать графические инструменты и калькуляторы для визуализации функции. Это поможет вам наглядно увидеть, как меняется объем при изменении параметров.

Вычисление площадей и объемов с помощью определённого интеграла
Проверяйте свои расчеты с помощью различных методов. Это позволяет убедиться в точности решения и дает уверенность в результате.
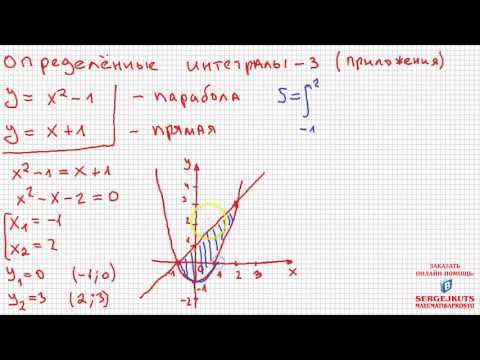
Математика без Ху%!ни. Определенные интегралы, часть 3. Площадь фигуры.

Для интегралов, которые не удается решить вручную, используйте численные методы, такие как метод трапеций или метод Симпсона.

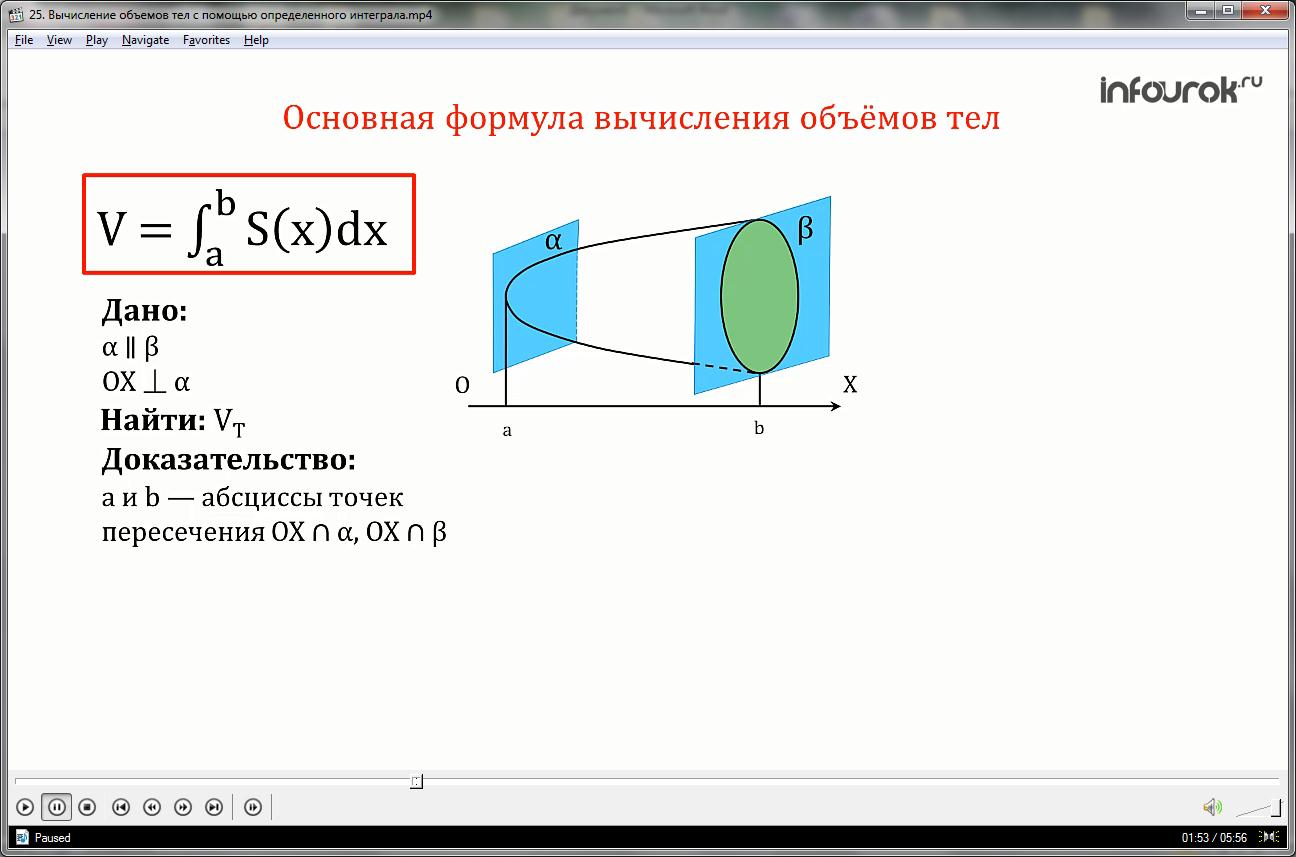
11 класс, 33 урок, Вычисление объемов тел с помощью определённого интеграла

Изучайте примеры решения задач по вычислению объемов. Чем больше примеров вы увидите, тем легче будет решать новые задачи.

Видеоурок \
И не забывайте об актуальных задачах с примерами, которые помогут вам усовершенствовать свои навыки в вычислениях объемов через интегралы.

Объем тела вращения на примере тора. 2 способа