Эффективные методы записи и анализа комплексных чисел
На этой странице вы найдете полезную подборку фотографий и советов, которые помогут лучше понять и использовать формы записи комплексных чисел в учебе или практике.
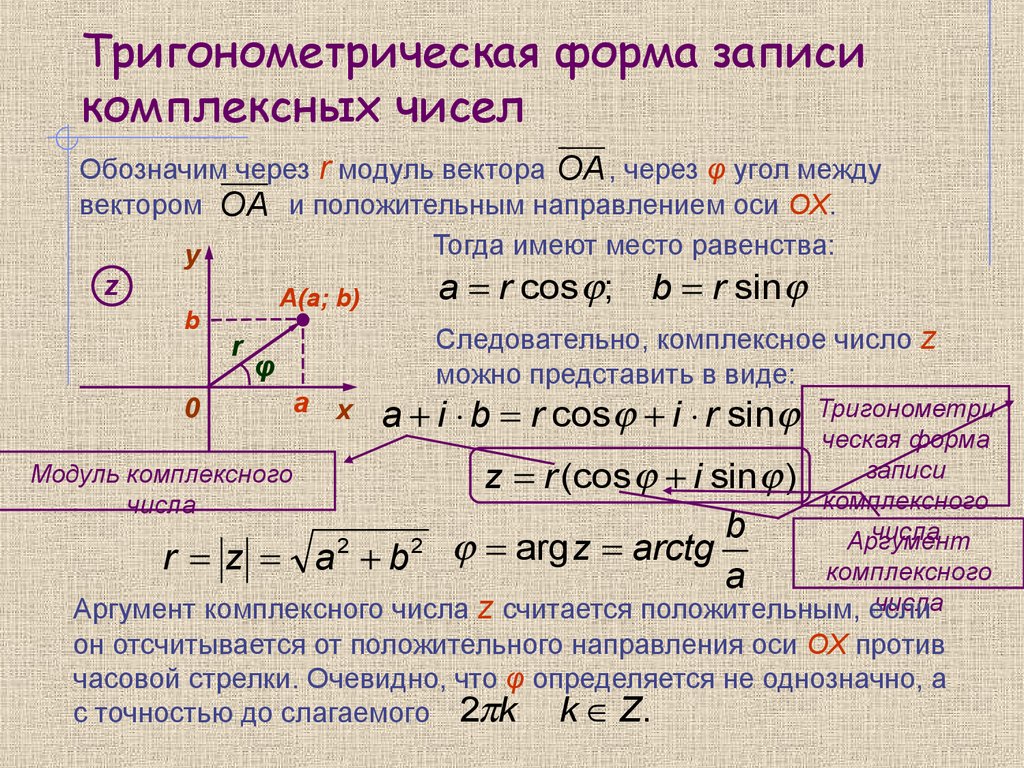


Начните с изучения алгебраической формы комплексного числа: z = a + bi, где a – действительная часть, а b – мнимая.

Тригонометрическая и показательная формы записи комплексного числа. Практика


Обратите внимание на тригонометрическую форму: z = r(cos(φ) + i*sin(φ)), где r – модуль, а φ – аргумент.

Комплексные числа. Тригонометрическая форма. Формула Муавра - Ботай со мной #040 - Борис Трушин !
Понимание экспоненциальной формы записи (z = re^(iφ)) поможет в работе с комплексными числами в физике и инженерии.

Тригонометрическая и показательная форма комплексного числа: Действия и Бонус - Высшая математика


Для нахождения модуля комплексного числа используйте формулу: |z| = √(a² + b²).

Тригонометрическая форма комплексного числа


Для аргумента числа можно использовать arctan(b/a), учитывая квадрант расположения числа.

Математика без Ху%!ни. Комплексные числа, часть 3. Формы записи. Возведение в степень.


Не забывайте использовать комплексно-сопряженные числа для упрощения деления: z₁/z₂ = (z₁ * z₂̅) / |z₂|².
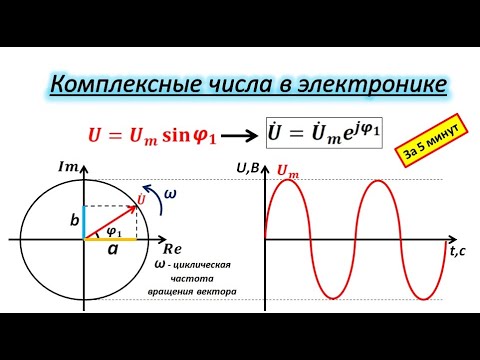
Комплексные числа в электронике/Показательная, тригонометрическая и алгебраическая форма


При умножении в тригонометрической форме просто перемножайте модули и складывайте аргументы.
КОМПЛЕКСНЫЕ ЧИСЛА ДЛЯ ЧАЙНИКОВ ЗА 7 МИНУТ

Для деления в тригонометрической форме делите модули и вычитайте аргументы.


Используйте графическое представление комплексных чисел в виде точек или векторов на комплексной плоскости для лучшего понимания.

ТРИГОНОМЕТРИЧЕСКАЯ ФОРМА ЗАПИСИ КОМПЛЕКСНОГО ЧИСЛА


Регулярно тренируйтесь переводить числа между алгебраической, тригонометрической и экспоненциальной формами для закрепления знаний.

10 класс, 34 урок, Тригонометрическая форма записи комплексного числа



Перевод комплексного числа из алгебраической формы в тригонометрическую, показательную